Utility UTILITY FUNCTIONS u A preference relation that

Utility

UTILITY FUNCTIONS u. A preference relation that is complete, reflexive, transitive and continuous can be represented by a continuous utility function (as an alternative, or as a complement, to the indifference “map” of the previous lecture). u Continuity means that small changes to a consumption bundle cause only small changes to the preference (utility) level.

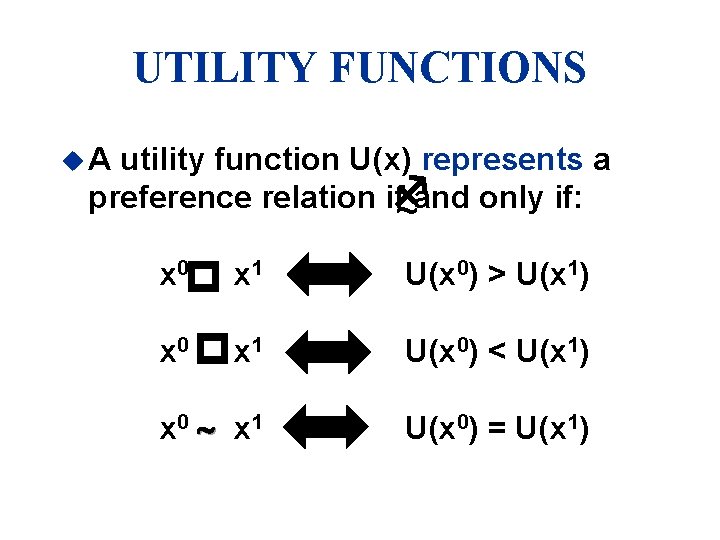
UTILITY FUNCTIONS u. A utility function U(x) represents a preference relation iff ~and only if: p x 0 x 1 U(x 0) > U(x 1) x 0 p x 1 U(x 0) < U(x 1) x 0 ~ x 1 U(x 0) = U(x 1)

UTILITY FUNCTIONS u Utility is an ordinal (i. e. ordering or ranking) concept. u For example, if U(x) = 6 and U(y) = 2 then bundle x is strictly preferred to bundle y. However, x is not necessarily “three times better” than y.

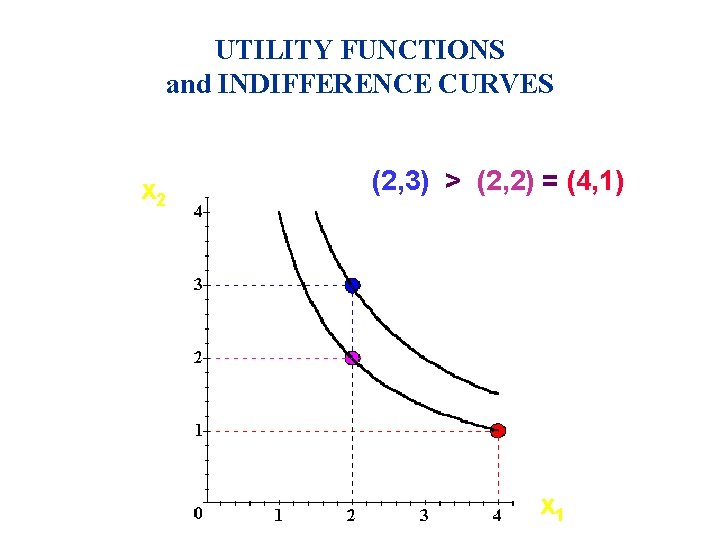
UTILITY FUNCTIONS and INDIFFERENCE CURVES u Consider the bundles (4, 1), (2, 3) and (2, 2). u Suppose (2, 3) > (4, 1) ~ (2, 2). u Assign to these bundles any numbers that preserve the preference ordering; e. g. U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4. u Call these numbers utility levels.

UTILITY FUNCTIONS and INDIFFERENCE CURVES u An indifference curve contains equally preferred bundles. preference same utility level. u Therefore, all bundles on an indifference curve have the same utility level. u Equal

UTILITY FUNCTIONS and INDIFFERENCE CURVES u So the bundles (4, 1) and (2, 2) are on the indifference curve with utility level U º 4 u But the bundle (2, 3) is on the indifference curve with utility level U º 6

UTILITY FUNCTIONS and INDIFFERENCE CURVES x 2 (2, 3) > (2, 2) = (4, 1) Uº 6 Uº 4 x 1 xx 1 1

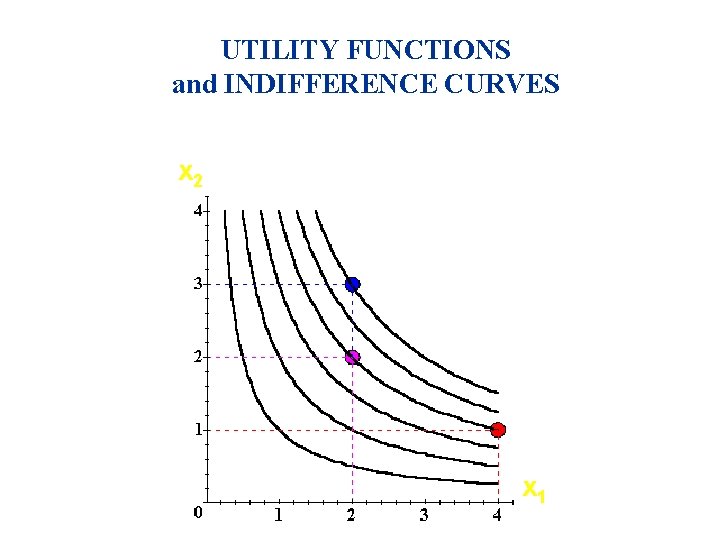
UTILITY FUNCTIONS and INDIFFERENCE CURVES u Comparing more bundles will create a larger collection of all indifference curves and a better description of the consumer’s preferences.

UTILITY FUNCTIONS and INDIFFERENCE CURVES x 2 x 2 Uº 6 Uº 4 Uº 2 xx 1 1

UTILITY FUNCTIONS and INDIFFERENCE CURVES u Comparing all possible consumption bundles gives the complete collection of the consumer’s indifference curves, each with its assigned utility level. u This complete collection of indifference curves completely represents the consumer’s preferences.

UTILITY FUNCTIONS and INDIFFERENCE CURVES u The collection of all indifference curves for a given preference relation is an indifference map. u An indifference map is equivalent to a utility function; each is the other.

UTILITY FUNCTIONS u If (i) U is a utility function that represents a preference relation; and (ii) f is a strictly increasing function, then V = f(U) is also a utility function representing the original preference function. Example? V = 2. U

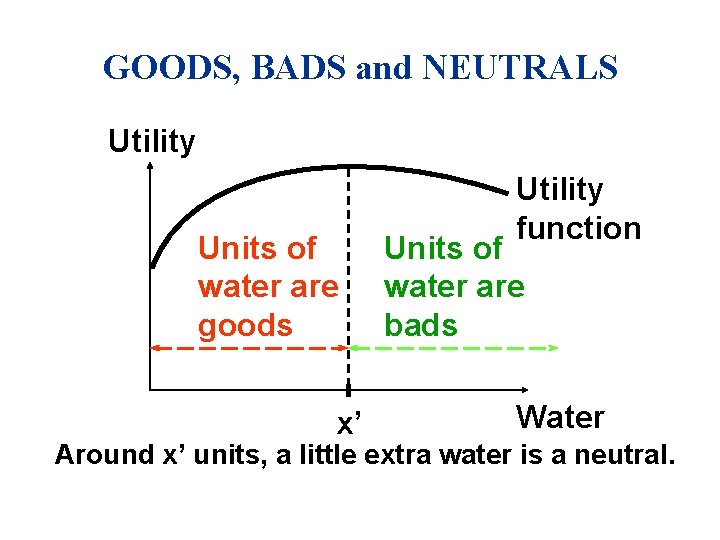
GOODS, BADS and NEUTRALS u. A good is a commodity unit which increases utility (gives a more preferred bundle). u A bad is a commodity unit which decreases utility (gives a less preferred bundle). u A neutral is a commodity unit which does not change utility (gives an equally preferred bundle).

GOODS, BADS and NEUTRALS Utility Units of water are goods x’ Utility function Units of water are bads Water Around x’ units, a little extra water is a neutral.

UTILITY FUNCTIONS Cobb-Douglas Utility Function Perfect Substitutes Utility Function Note: MRS = (-)a/b Perfect Complements Utility Function Note: MRS = ?

UTILITY Preferences can be represented by a utility function if the functional form has certain “nice” properties Example: Consider U(x 1, x 2)= x 1. x 2 1. 2. u/ x 1>0 and u/ x 2>0 Along a particular indifference curve x 1. x 2 = constant x 2=c/x 1 As x 1 x 2 i. e. downward sloping indifference curve

UTILITY Example U(x 1, x 2)= x 1. x 2 =16 X 1 X 2 MRS 1 16 2 8 (-) 8 3 5. 3 (-) 2. 7 4 4 (-) 1. 3 5 3. 2 (-) 0. 8 3. As X 1 MRS (in absolute terms), i. e convex preferences

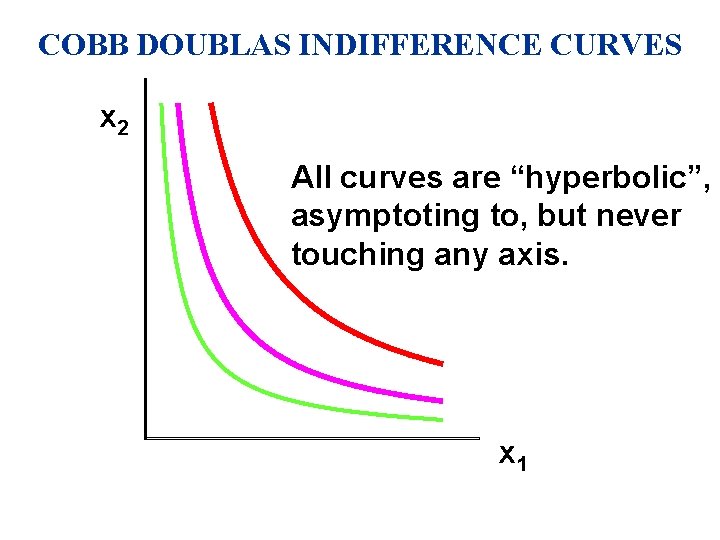
COBB DOUGLAS UTILITY FUNCTION u Any utility function of the form U(x 1, x 2) = x 1 a x 2 b with a > 0 and b > 0 is called a Cobb. Douglas utility function. u Examples U(x 1, x 2) = x 11/2 x 21/2 (a = b = 1/2) V(x 1, x 2) = x 1 x 23 (a = 1, b = 3)

COBB DOUBLAS INDIFFERENCE CURVES x 2 All curves are “hyperbolic”, asymptoting to, but never touching any axis. x 1

PERFECT SUBSITITUTES u Instead of U(x 1, x 2) = x 1 x 2 consider V(x 1, x 2) = x 1 + x 2.

PERFECT SUBSITITUTES x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2 5 9 13 x 1 All are linear and parallel.

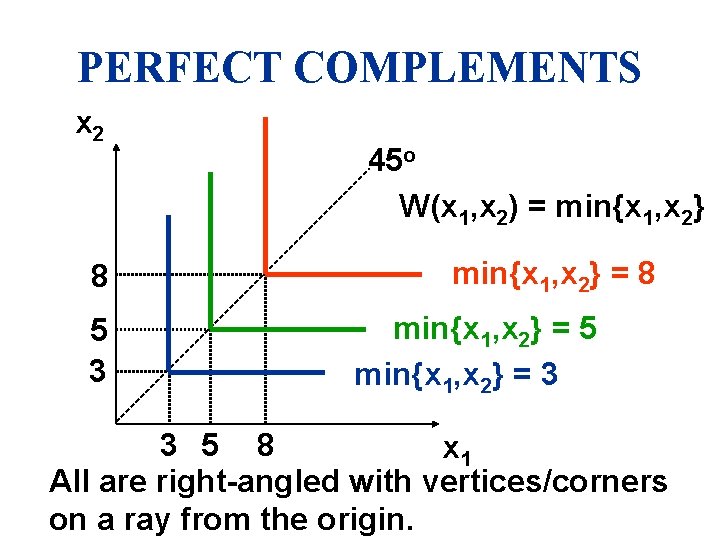
PERFECT COMPLEMENTS u Instead of U(x 1, x 2) = x 1 x 2 or V(x 1, x 2) = x 1 + x 2, consider W(x 1, x 2) = min{x 1, x 2}.

PERFECT COMPLEMENTS x 2 8 5 3 45 o W(x 1, x 2) = min{x 1, x 2} = 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 3 5 8 x 1 All are right-angled with vertices/corners on a ray from the origin.

MARGINAL UTILITY u Marginal means “incremental”. u The marginal utility of product i is the rate-of-change of total utility as the quantity of product i consumed changes by one unit; i. e.

MARGINAL UTILITY U=(x 1, x 2) MU 1= U/ x 1 U=MU 1. x 1 MU 2= U/ x 2 U=MU 2. x 2 Along a particular indifference curve U = 0 = MU 1( x 1) + MU 2( x 2) x 2/ x 1 {= MRS} = (-)MU 1/MU 2

MARGINAL UTILITY u E. g. if U(x 1, x 2) = x 11/2 x 22 then

MARGINAL UTILITY u E. g. if U(x 1, x 2) = x 11/2 x 22 then

MARGINAL UTILITY u E. g. if U(x 1, x 2) = x 11/2 x 22 then

MARGINAL UTILITY u E. g. if U(x 1, x 2) = x 11/2 x 22 then

MARGINAL UTILITY u So, if U(x 1, x 2) = x 11/2 x 22 then

MARGINAL UTLITIES AND MARGINAL RATE OF SUBISITUTION u The general equation for an indifference curve is U(x 1, x 2) º k, a constant u Totally differentiating this identity gives

MARGINAL UTLITIES AND MARGINAL RATE OF SUBISITUTION rearranging

MARGINAL UTLITIES AND MARGINAL RATE OF SUBISITUTION rearranging This is the MRS.

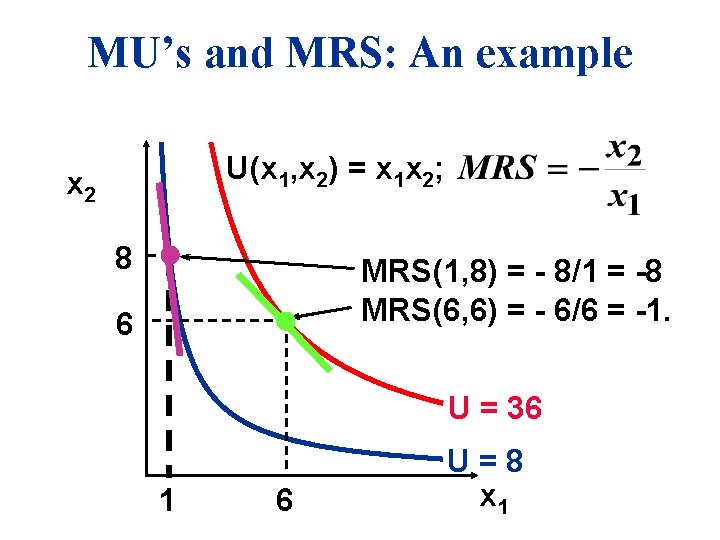
MU’s and MRS: An example Suppose U(x 1, x 2) = x 1 x 2. Then so

MU’s and MRS: An example U(x 1, x 2) = x 1 x 2; x 2 8 MRS(1, 8) = - 8/1 = -8 MRS(6, 6) = - 6/6 = -1. 6 U = 36 1 6 U=8 x 1

MONOTONIC TRANSFORMATIONS AND MRS u Applying a monotonic transformation to a utility function representing a preference relation simply creates another utility function representing the same preference relation. u What happens to marginal rates-ofsubstitution when a monotonic transformation is applied? (Hopefully, nothing)

MONOTONIC TRANSFORMATIONS AND MRS u For U(x 1, x 2) = x 1 x 2 the MRS = (-) x 2/x 1 u Create V = U 2; i. e. V(x 1, x 2) = x 12 x 22 What is the MRS for V? which is the same as the MRS for U.

MONOTONIC TRANSFORMATIONS AND MRS u More generally, if V = f(U) where f is a strictly increasing function, then So MRS is unchanged by a positive monotonic transformation.