Utility Theory Stephen Chiu University of Hong Kong

Utility Theory Stephen Chiu University of Hong Kong 1

Utility Theory n The cardinal approach n The ordinal approach n Consumer choice problem n Intertemporal choice problem 2

The cardinal approach n In the 18 th century, Bentham proposed that the objective of public policy should be to maximize the sum of happiness in society n Economics became the study of utility or happiness, assumed to be in principle measurable and comparable across people n Marginal utility of income was higher for poor people than for rich people, so that income ought to be redistributed unless the efficiency cost was too high 3

The ordinal approach n Lionel Robbins (in 1932) argued that, n Comparability of utility across people is not needed so long we are concerned about predicting choices n Economics is about “the relationship between given ends and scarce means”, and how the “ends” or preferences came to be formed was outside its scope n Only stable preferences are needed n Robbins didn’t think that public policy could be analyzed within a formal economic framework 4

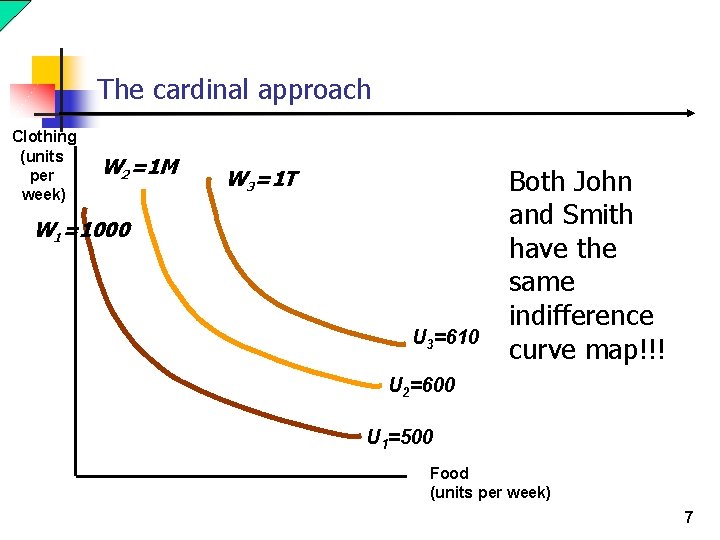
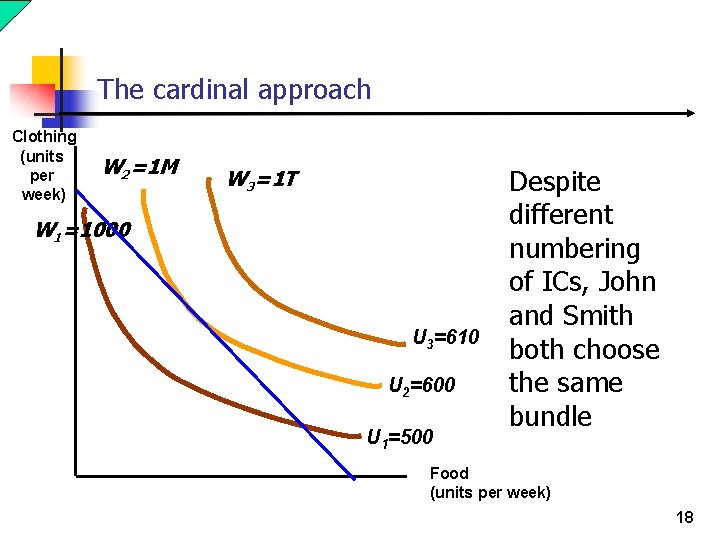
The cardinal approach n An agent’s utility level is like length or weight of an object that is objective and measurable n An agent with utility level 3, 000 is happier than another agent with utility level 200 n But … John always looks happy and enthusiastic, and Smith unhappy and worrisome… 5

The cardinal approach n They both come to class. . . n … given the same income and prices, John always spends his income the same way as Smith does 6

The cardinal approach Clothing (units per week) W 2=1 M W 3=1 T W 1=1000 U 3=610 Both John and Smith have the same indifference curve map!!! U 2=600 U 1=500 Food (units per week) 7

Why diversity in consumption? n Cardinal approach – diversity because of diminishing marginal utility n Ordinal approach – diversity despite no diminishing marginal utility; what is needed is MU/$ being equalized 8

Consumer Choice problem n Ordinal utility function n indifference curve map n Numbering of ICs unimportant, as long as they are order preserving n Some regularity conditions (a. k. a. axioms) on ICs n Budget constraint n The problem becomes to max utility subject to budget constraint 9

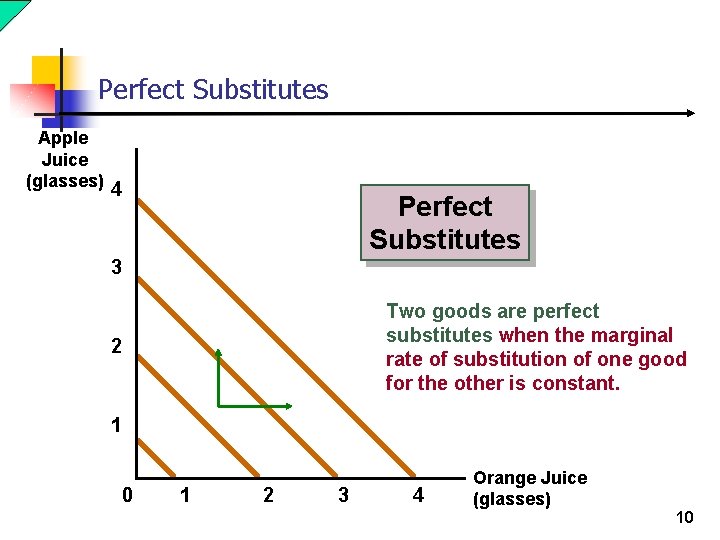
Perfect Substitutes Apple Juice (glasses) 4 Perfect Substitutes 3 Two goods are perfect substitutes when the marginal rate of substitution of one good for the other is constant. 2 1 0 1 2 3 4 Orange Juice (glasses) 10

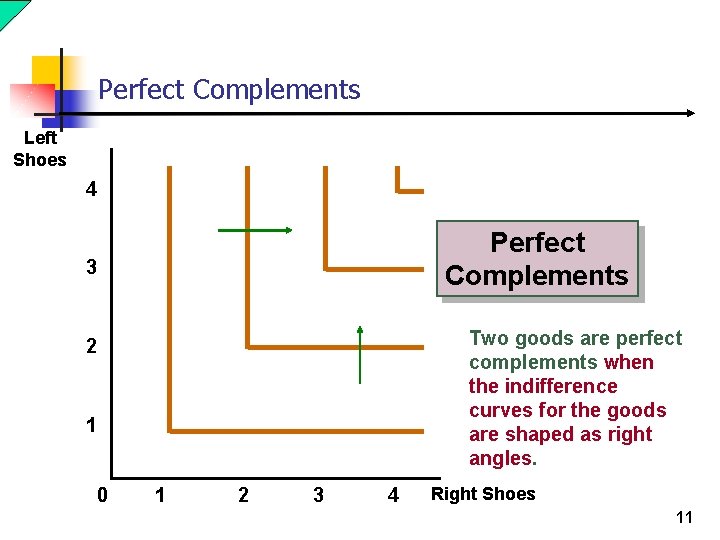
Perfect Complements Left Shoes 4 Perfect Complements 3 Two goods are perfect complements when the indifference curves for the goods are shaped as right angles. 2 1 0 1 2 3 4 Right Shoes 11

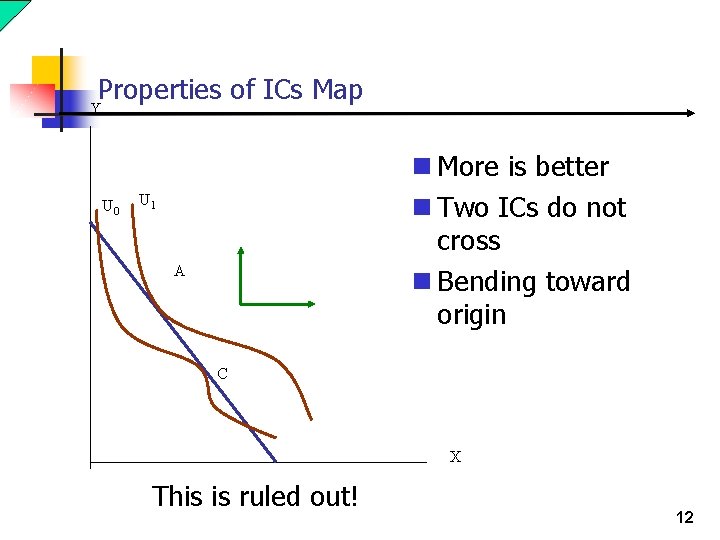
Properties of ICs Map Y U 0 n More is better n Two ICs do not cross n Bending toward origin U 1 A C X This is ruled out! 12

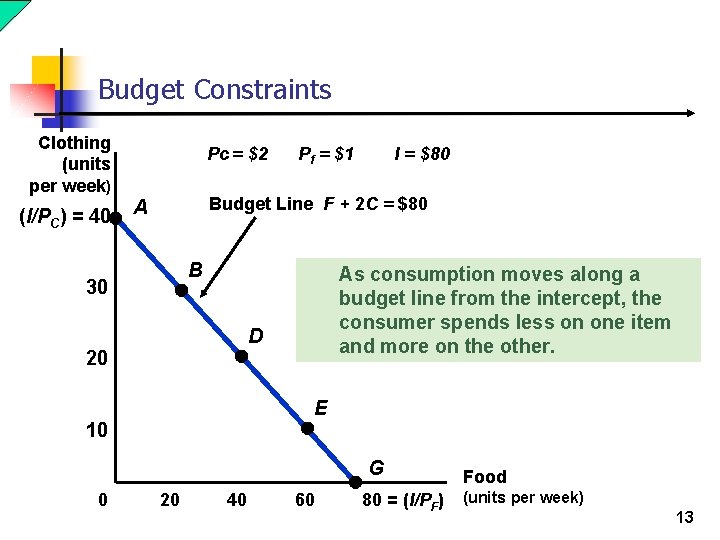
Budget Constraints Clothing (units per week) (I/PC) = 40 Pc = $2 Pf = $1 I = $80 Budget Line F + 2 C = $80 A B 30 As consumption moves along a budget line from the intercept, the consumer spends less on one item and more on the other. D 20 E 10 G 0 20 40 60 80 = (I/PF) Food (units per week) 13

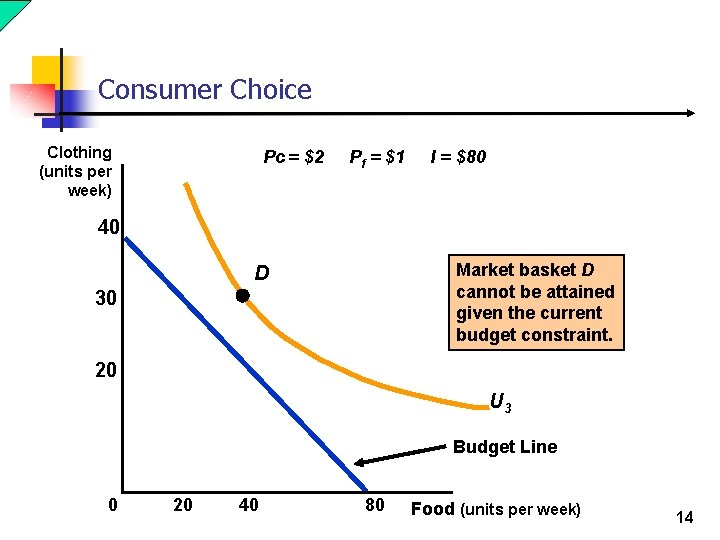
Consumer Choice Clothing (units per week) Pc = $2 Pf = $1 I = $80 40 Market basket D cannot be attained given the current budget constraint. D 30 20 U 3 Budget Line 0 20 40 80 Food (units per week) 14

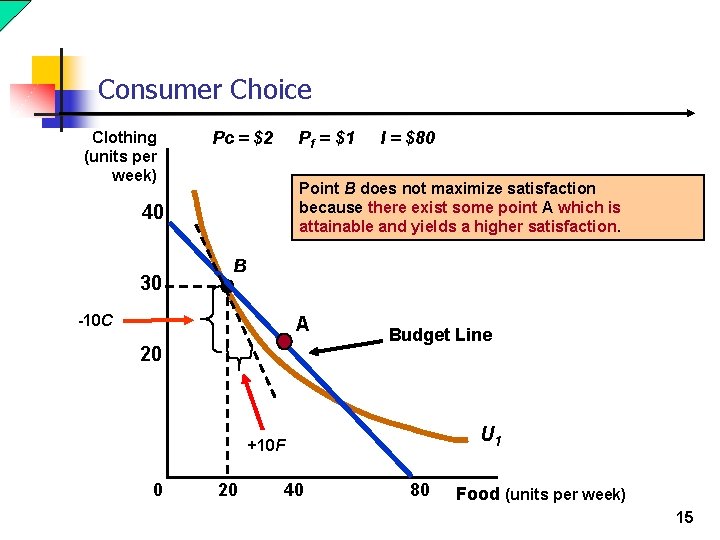
Consumer Choice Clothing (units per week) Pc = $2 Pf = $1 Point B does not maximize satisfaction because there exist some point A which is attainable and yields a higher satisfaction. 40 30 I = $80 B -10 C A 20 Budget Line U 1 +10 F 0 20 40 80 Food (units per week) 15

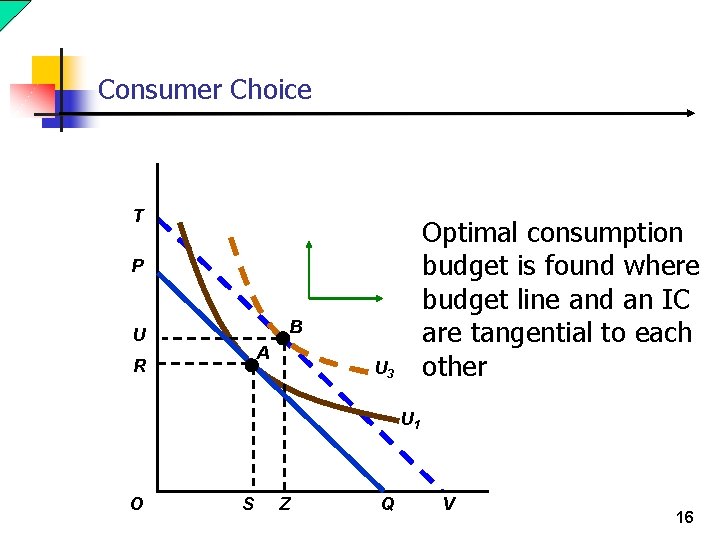
Consumer Choice T Optimal consumption budget is found where budget line and an IC are tangential to each other P B U A R U 3 U 1 O S Z Q V 16

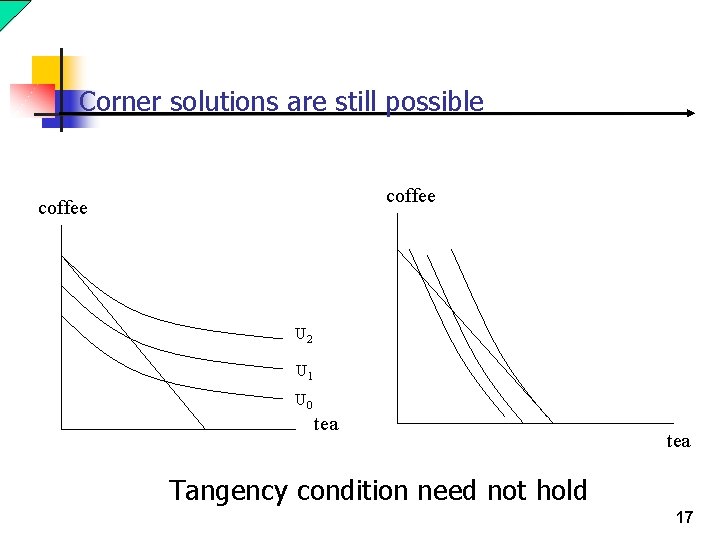
Corner solutions are still possible coffee U 2 U 1 U 0 tea Tangency condition need not hold 17

The cardinal approach Clothing (units per week) W 2=1 M W 3=1 T W 1=1000 U 3=610 U 2=600 U 1=500 Despite different numbering of ICs, John and Smith both choose the same bundle Food (units per week) 18

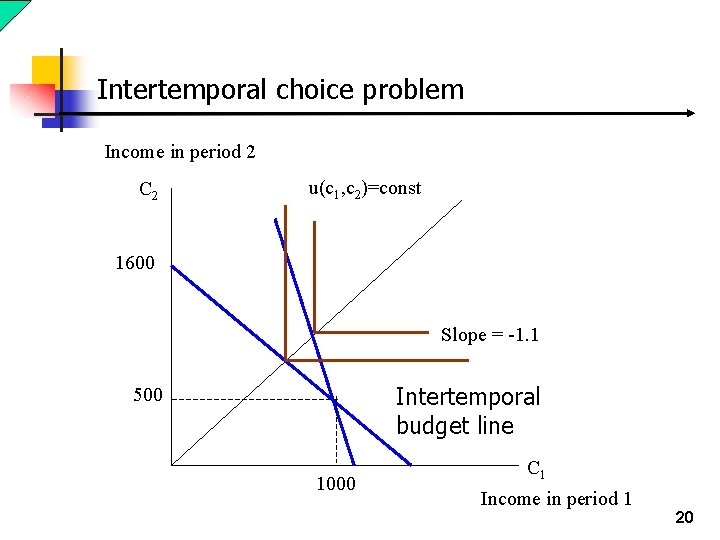
An application: Intertemporal Choice n Our framework is flexible enough to deal with questions such as savings decisions and intertemporal choice. n Suppose you live two periods: period 1 and period 2 n You earn an income of 1, 000 in period 1 and a pension of 500 in period 2 n Interest rate r. That is, by saving $1 in period 1, you get back $(1+r) in period 2 n You consider period 1 consumption and period 2 consumption perfect complement n Question: how much should you save now? 19

Intertemporal choice problem Income in period 2 C 2 u(c 1, c 2)=const 1600 Slope = -1. 1 Intertemporal budget line 500 1000 C 1 Income in period 1 20

Intertemporal choice problem 1000 -C 1=S 500+S(1+r)=C 2 Substituting (1) into (2), we have 500+(1000 -C 1)(1+r)=C 2 Rearranging, we have 1500+1000 r-(1+r) C 1=C 2 > C Using C 1=C 2=C, we finally have (1) (2) 21

Conclusions n Ordinal utility theory is good enough so long as we want to study choice n Cardinal utility theory is needed if we want to study public policy n Happiness = subjective well being n Happiness survey shows that average happiness in a nation remains the same level once per capita income reaches a certain level n More on happiness if time permitted 22