usually unimportant in social surveys n 10 000

• usually unimportant in social surveys: n =10, 000 and N = 5, 000: 1 - f = 0. 998 n =1000 and N = 400, 000: 1 - f = 0. 9975 n =1000 and N = 5, 000: 1 -f = 0. 9998 • effect of changing n much more important than effect of changing n/N 1

The estimated variance Usually we report the standard error of the estimate: Confidence intervals for m Central Limit Theorem: is based on the 2

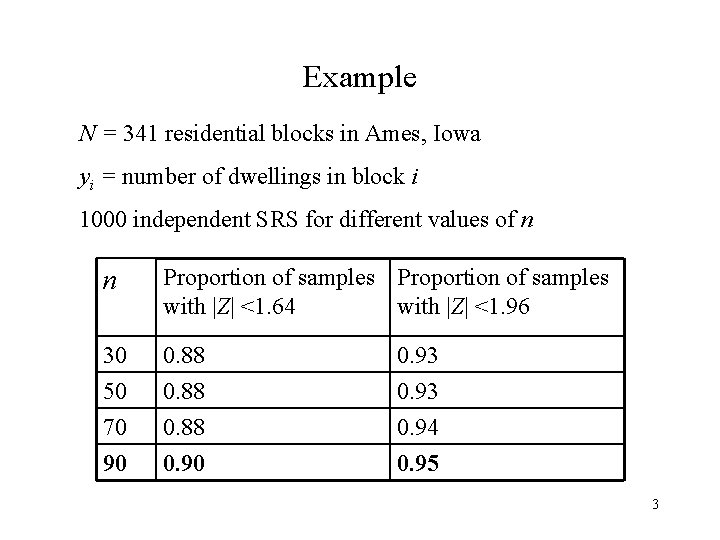
Example N = 341 residential blocks in Ames, Iowa yi = number of dwellings in block i 1000 independent SRS for different values of n n Proportion of samples with |Z| <1. 64 with |Z| <1. 96 30 50 0. 88 0. 93 70 90 0. 88 0. 90 0. 94 0. 95 3

For one SRS with n = 90: 4

Absolute value of sampling error is not informative when not related to value of the estimate For example, SE =2 is small if estimate is 1000, but very large if estimate is 3 The coefficient of variation for the estimate: • A measure of the relative variability of an estimate. • It does not depend on the unit of measurement. • More stable over repeated surveys, can be used for planning, for example determining sample size • More meaningful when estimating proportions 5

Estimation of a population proportion p with a certain characteristic A p = (number of units in the population with A)/N Let yi = 1 if unit i has characteristic A, 0 otherwise Then p is the population mean of the yi’s. Let X be the number of units in the sample with characteristic A. Then the sample mean can be expressed as 6

So the unbiased estimate of the variance of the estimator: 7

Examples A political poll: Suppose we have a random sample of 1000 eligible voters in Norway with 280 saying they will vote for the Labor party. Then the estimated proportion of Labor votes in Norway is given by: Confidence interval requires normal approximation. Can use the guideline from binomial distribution, when N-n is large: 8

In this example : n = 1000 and N = 4, 000 Ex: Psychiatric Morbidity Survey 1993 from Great Britain p = proportion with psychiatric problems n = 9792 (partial nonresponse on this question: 316) N@ 40, 000 9

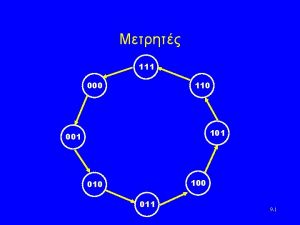
General probability sampling • Sampling design: p(s) - known probability of selection for each subset s of the population U • Actually: The sampling design is the probability distribution p(. ) over all subsets of U • Typically, for most s: p(s) = 0. In SRS of size n, all s with size different from n has p(s) = 0. • The inclusion probability: 10

Illustration U = {1, 2, 3, 4} Sample of size 2; 6 possible samples Sampling design: p({1, 2}) = ½, p({2, 3}) = 1/4, p({3, 4}) = 1/8, p({1, 4}) = 1/8 The inclusion probabilities: 11

Some results 12

Estimation theory probability sampling in general Problem: Estimate a population quantity for the variable y For the sake of illustration: The population total 13

CV is a useful measure of uncertainty, especially when standard error increases as the estimate increases Because, typically we have that 14

Some peculiarities in the estimation theory Example: N=3, n=2, simple random sample 15

For this set of values of the yi’s: 16

Let y be the population vector of the y-values. This example shows that is not uniformly best ( minimum variance for all y) among linear design-unbiased estimators Example shows that the ”usual” basic estimators do not have the same properties in design-based survey sampling as they do in ordinary statistical models In fact, we have the following much stronger result: Theorem: Let p(. ) be any sampling design. Assume each yi can take at least two values. Then there exists no uniformly best design-unbiased estimator of the total t 17

Proof: This implies that a uniformly best unbiased estimator must have variance equal to 0 for all values of y, which is impossible 18