Using the Stream Bit Compiler to Optimize your

Using the Stream. Bit Compiler to Optimize your programs Armando Solar-Lezama, Rastislav Bodik UC Berkeley 1

What’s wrong with using C? • You could write a SETBIT and GETBIT macros to make it easy to read and write individual bits – #define getbit( a, i) (( a & ( 0 x 80000000 >> i )) > 0) – #define setbit( a, i, v) a = v ? (( a | ( 0 x 80000000 >> i ))) : (( a & ~( 0 x 80000000 >> i ))) • Write your code in terms of individual bits without loosing much performance by using the macros. – Unfortunately it doesn’t quite work. – Performance can be 10 x worse than hand-tuned solution 2

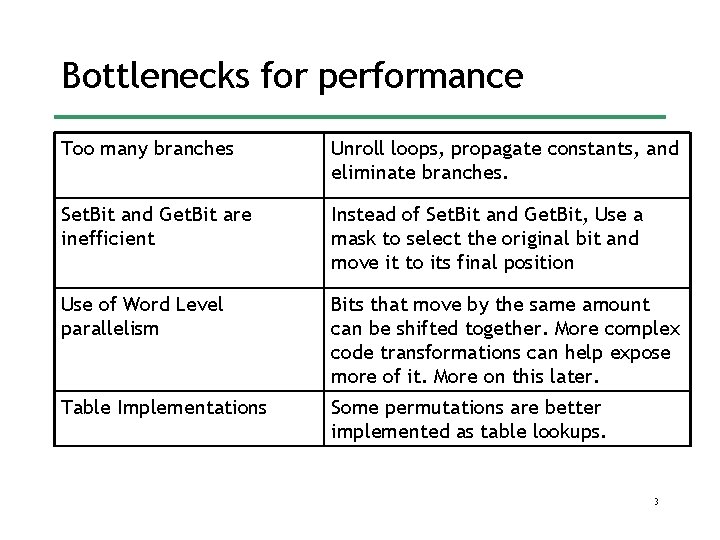
Bottlenecks for performance Too many branches Unroll loops, propagate constants, and eliminate branches. Set. Bit and Get. Bit are inefficient Instead of Set. Bit and Get. Bit, Use a mask to select the original bit and move it to its final position Use of Word Level parallelism Bits that move by the same amount can be shifted together. More complex code transformations can help expose more of it. More on this later. Table Implementations Some permutations are better implemented as table lookups. 3

Bottlenecks for performance Too many branches Unroll loops, propagate constants, and eliminate branches. Set. Bit and Get. Bit are inefficient Instead of Set. Bit and Get. Bit, Use a mask to select the original bit and move it to its final position • In the case of C, the first two are straightforward, but you have to be careful with typos. • The two are handled completely automatically by the Stream. Bit compiler. 4

Bottlenecks for performance Use of Word Level parallelism Bits that move by the same amount can be shifted together. More complex code transformations can help expose more of it. More on this later. Table Implementations Some tables are better implemented as table lookups. • The performance effects of these two are hard to predict – Increasing parallelism at the word level may introduce dependencies between instructions – Table implementations introduce cache effects. • With Stream. Bit, they can be expressed conveniently with sketching, using the Transformation Specification Language. 5

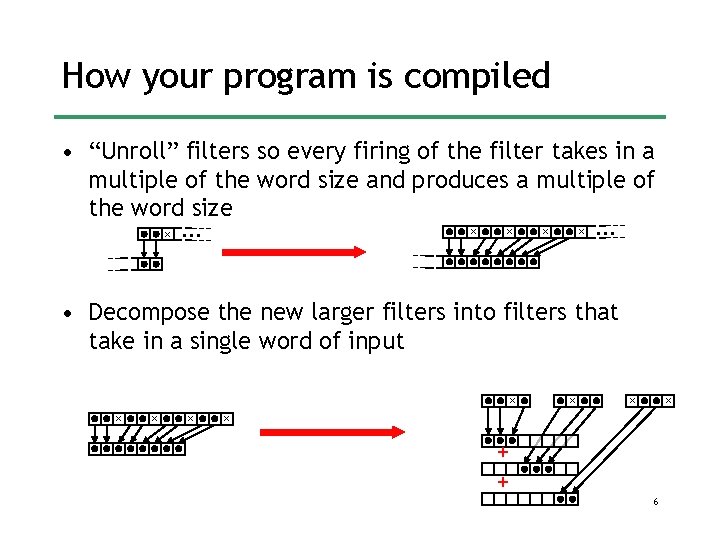
How your program is compiled • “Unroll” filters so every firing of the filter takes in a multiple of the word size and produces a multiple of the word size x . . . x x . . . • Decompose the new larger filters into filters that take in a single word of input x x x x + + 6

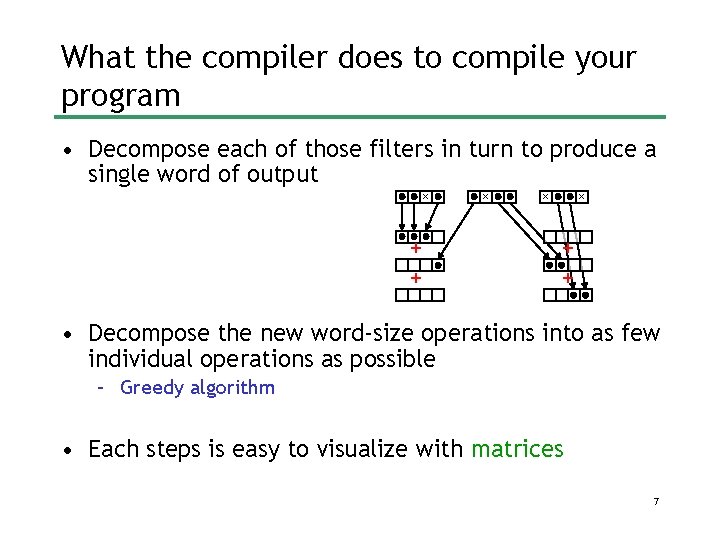
What the compiler does to compile your program • Decompose each of those filters in turn to produce a single word of output x + + x x x + + • Decompose the new word-size operations into as few individual operations as possible – Greedy algorithm • Each steps is easy to visualize with matrices 7

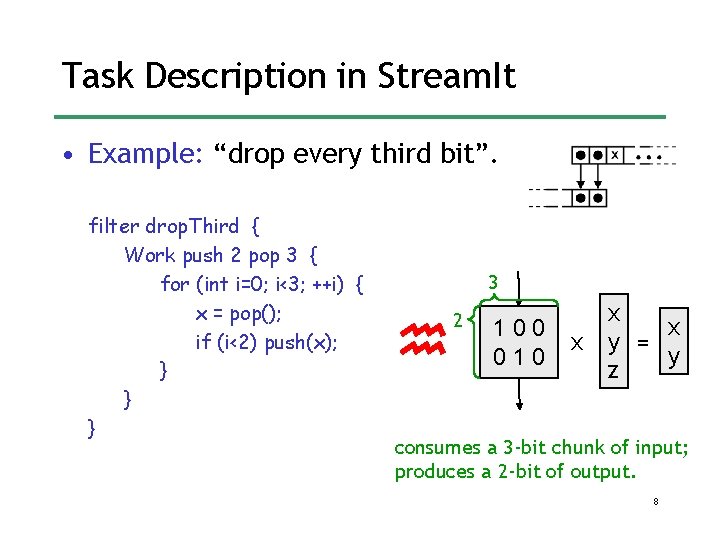
Task Description in Stream. It • Example: “drop every third bit”. filter drop. Third { Work push 2 pop 3 { for (int i=0; i<3; ++i) { x = pop(); if (i<2) push(x); } } } 3 2 100 010 x x x y = y z consumes a 3 -bit chunk of input; produces a 2 -bit of output. 8

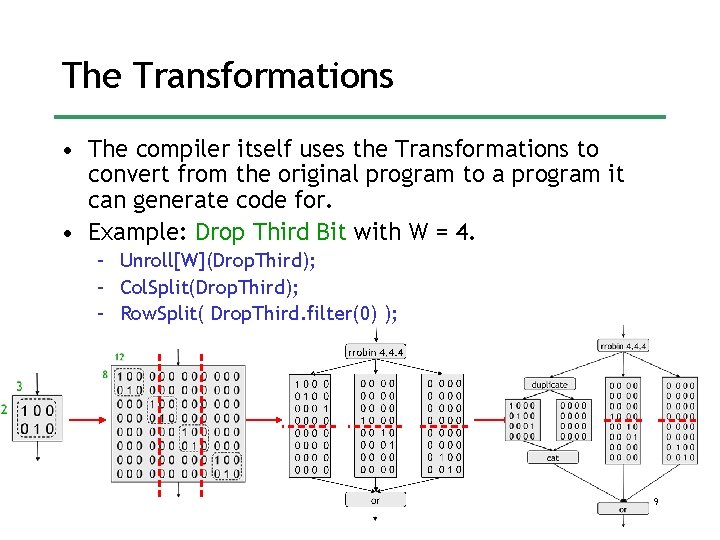
The Transformations • The compiler itself uses the Transformations to convert from the original program to a program it can generate code for. • Example: Drop Third Bit with W = 4. – Unroll[W](Drop. Third); – Col. Split(Drop. Third); – Row. Split( Drop. Third. filter(0) ); 9

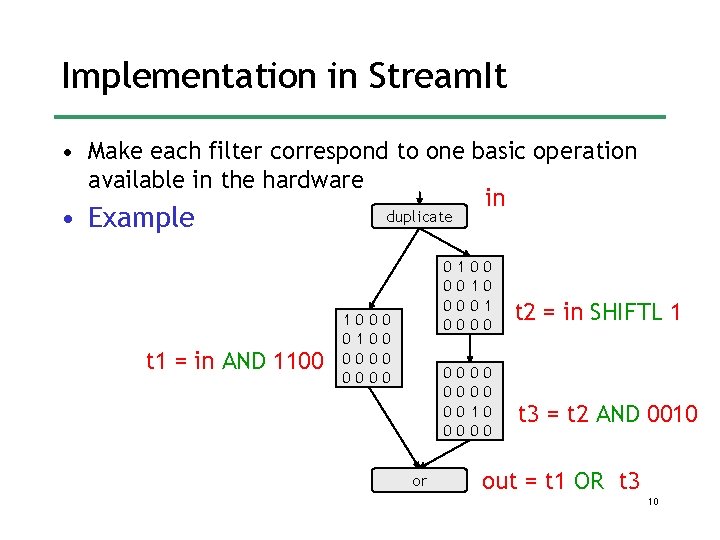
Implementation in Stream. It • Make each filter correspond to one basic operation available in the hardware in • Example t 1 = in AND 1100 duplicate 1 0 0 0 0 or 0 0 0 0 1 0 0 0 1 0 0 0 t 2 = in SHIFTL 1 t 3 = t 2 AND 0010 out = t 1 OR t 3 10

Default Implementation • Automatic Transform algorithm • Defines a default implementation for any program • Leveraged by the user for more involved implementations – How? HL program LL program 11

An Example • In some cases, It is possible to improve the use of the word by decomposing the permutation into steps. Drop Third • Example SLOW O(w) FAST O(log w) 12

An Example • How do we tell the compiler about this? – We need to be able to refer to the filter we want to transform – We need to tell the compiler what we want it to do • We don’t want to tell the compiler exactly how to do it, the compiler can figure it out. sketch – We want to be sure we won’t introduce bugs ? ? ? ? ? ? ? FAST ? ? implementation ? ? functionality ? ? ? ? + ? ? ? ? 13

The Transformation Specification Language (TSL): The basics • Three main components – Filter paths • Allow you to refer to any filter in your program – Transformation Functions • Apply a transformation on their argument • Also included in this category are display functions that allow you to see the result of your transformations – Control and basic integer arithmetic • For control, we currently support only for loops • Basic integer arithmetic includes addition, subtraction, and multiplication. • Variables don’t have to be declared 14

Filter Paths • The path for a filter is defined as follows – For the top level filter it’s its name – For all other filters, the path can either be: parent_path. filter_name or parent_path. filter( i ) • Where parent_path is the path to the pipeline or splitjoin that contains the filter in question and i is the position of the filter in that pipeline or splitjoin – Paths with numeric indices are convenient for loops. – Paths with names are easier to read. 15

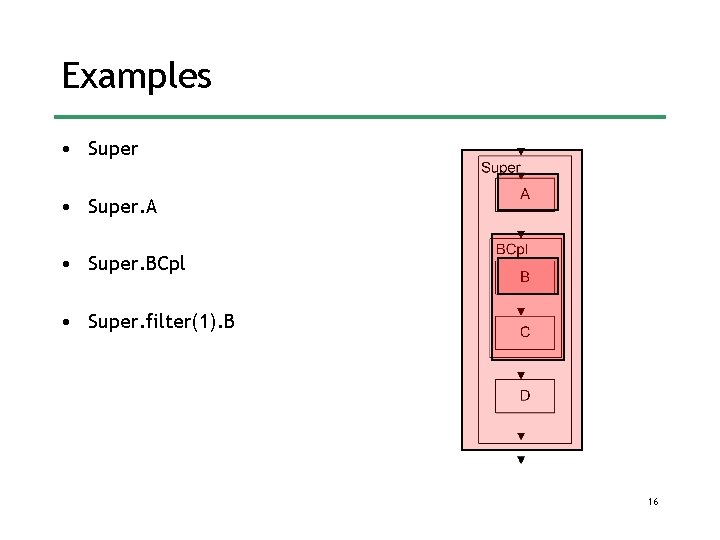
Examples • Super. A • Super. BCpl • Super. filter(1). B 16

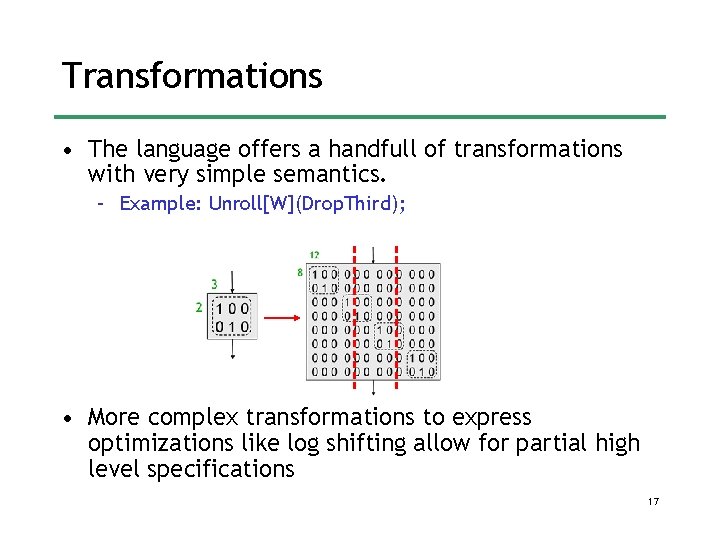
Transformations • The language offers a handfull of transformations with very simple semantics. – Example: Unroll[W](Drop. Third); • More complex transformations to express optimizations like log shifting allow for partial high level specifications 17

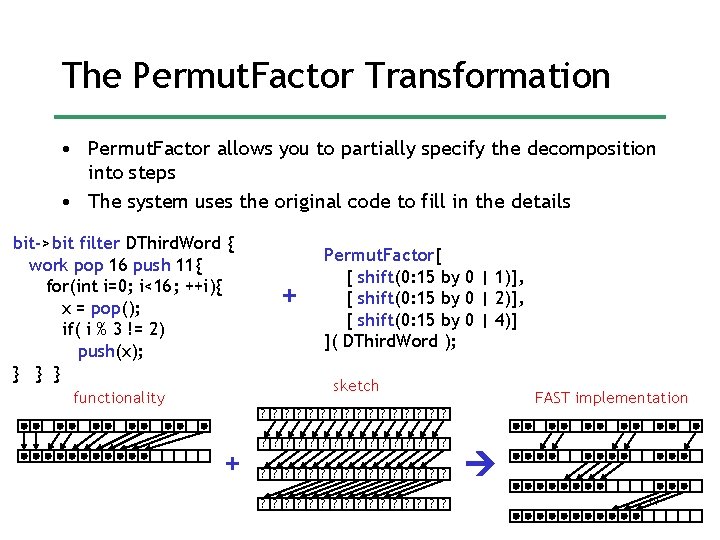
The Permut. Factor Transformation • Permut. Factor allows you to partially specify the decomposition into steps • The system uses the original code to fill in the details bit->bit filter DThird. Word { work pop 16 push 11{ for(int i=0; i<16; ++i){ x = pop(); if( i % 3 != 2) push(x); } } } functionality + Permut. Factor[ [ shift(0: 15 by 0 | 1)], [ shift(0: 15 by 0 | 2)], [ shift(0: 15 by 0 | 4)] ]( DThird. Word ); sketch FAST implementation ? ? ? ? + ? ? ? ? ? ? ? ? ? ? ? ? 19

More on Permut. Factor • The Permut. Factor function specifies each step as a list of constraints – Permut. Factor[ [constr. List], …] • Constraints of 4 types: – Type 1: specific shift amount • shift( bit. List by x) – Type 2: undetermined shift amount • shift( bit. List by ? ) – Type 3: limited choice of shift amount • shift( bit. List by a || b || …) – Type 4: Specify the position of the bits • pos( bit. List to pos. List) • System ignores constraints on discarded bits 20

Restructuring To Improve Performance • Several kinds of restructuring can be done to improve performance – Merge Several Matrix Filters together into a single filter that can be implemented more efficiently – Merge a filter into a Round. Robin Spliter or Joiner to improve its performance • All of these restructurings are possible through the Restructure Function. 21

Example • Restructure[ A , [“BCpl”, B, C], D](Super) – Note that A, B, C, D are refered to by their names local to Super. – The same effect could be achieved with • Restructure[ A , [“BCpl”, filter(1), filter(2)], D](Super) 22

Example • Restructure[ A , Merge[Matrix, “BC”, B, C], D](Super) – Now, B and C were merged into a single matrix. – NOTE: When applying restructurings, the Print Command is very effective to allow you to see how your pipeline looks like before and after. 23

Restructure: How it works • Restructure takes a filter and a list of filter. Specs and returns a pipeline with one filter for every filter. Spec – Restructure[ filter. Spec, …](filter) • A filter spec can be any of the following – The local name of a descendant of filter – A list of filter. Specs enclosed in brackets – A Merge Specification • Merge[ type, “Name”, filter, …] • The type indicates whether you want to merge the filters into: – Matrix: a single matrix – Splitjoin: a splitjoin – Pipeline: a pipeline; Equivalent to simply writing [filter, filter…] 24

Table Implementations • In many cases, a Table implementation of a Filter, or even of a whole pipeline, is the most effective way to achieve performance • The Make. Table command can take a filter and convert it into a Table. – You should not call this command for filters with an input size that is too big, since the table will be of size 2^insize – You can use Col. Split to break a fitler into smaller filters which can be implemented with tables 25

Conclusion • The Transformation Specification Language allows you to optimize your program without having to modify your code. • The choice of optimizations will depend heavily on many characteristics of the machine, but the TSL allows you to try several different implementations with relatively little effort 26