Using the Standard Normal Distribution to Solve SPC

Using the Standard Normal Distribution to Solve SPC Problems q Table A. 1: “Areas Under the Normal Curve” ISE 327 Ch. 3 Homework 1

Applications of the Normal Distribution q A certain machine makes electrical resistors having a mean resistance of 40 ohms and a standard deviation of 2 ohms. What percentage of the resistors will have a resistance less than 44 ohms? q Solution: X is normally distributed with μ = 40 and σ = 2 and x = 44 P(X<44) = P(Z< +2. 0) = 0. 9772 Therefore, we conclude that 97. 72% will have a resistance less than 44 ohms. What percentage will have a resistance greater than 44 ohms? ISE 327 Ch. 3 Homework 2

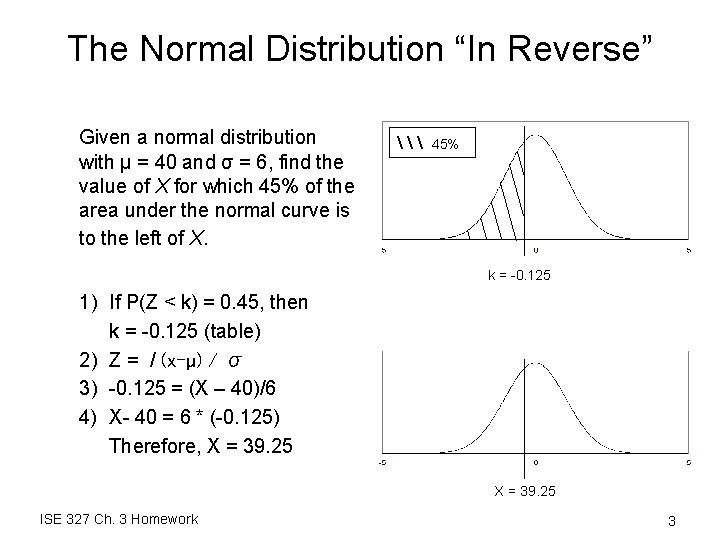
The Normal Distribution “In Reverse” Given a normal distribution with μ = 40 and σ = 6, find the value of X for which 45% of the area under the normal curve is to the left of X. \ 45% k = -0. 125 1) If P(Z < k) = 0. 45, then k = -0. 125 (table) 2) Z = / (x-µ) / σ 3) -0. 125 = (X – 40)/6 4) X- 40 = 6 * (-0. 125) Therefore, X = 39. 25 ISE 327 Ch. 3 Homework 3

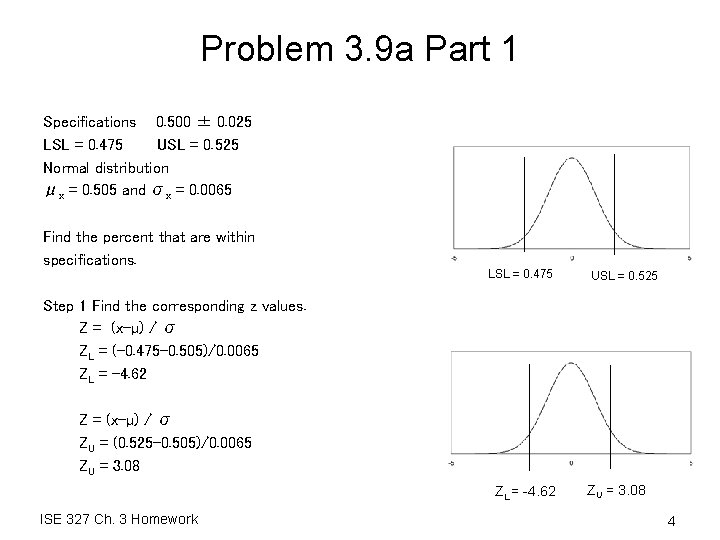
Problem 3. 9 a Part 1 Specifications 0. 500 ± 0. 025 LSL = 0. 475 USL = 0. 525 Normal distribution μx = 0. 505 and σx = 0. 0065 Find the percent that are within specifications. LSL = 0. 475 USL = 0. 525 Step 1 Find the corresponding z values. Z = (x-µ) / σ ZL = (-0. 475 -0. 505)/0. 0065 ZL = -4. 62 Z = (x-µ) / σ ZU = (0. 525 -0. 505)/0. 0065 ZU = 3. 08 ZL = -4. 62 ISE 327 Ch. 3 Homework ZU = 3. 08 4

Problem 3. 9 a Part 2 Specifications 0. 500 ± 0. 025 LSL = 0. 475 USL = 0. 525 Normal distribution μx = 0. 505 and σx = 0. 0065 Find the percent that are within specifications. Step 2 Find the area under the curve between the LSL and USL. LSL = 0. 475 USL = 0. 525 P(Z 3. 08) - P(Z -4. 62) = 0. 99897 – 0. 0 = 0. 99897 Therefore 99. 897% are within specifications. What percent are outside of specifications? 99. 897% ZL = -4. 62 ISE 327 Ch. 3 Homework ZU = 3. 08 5

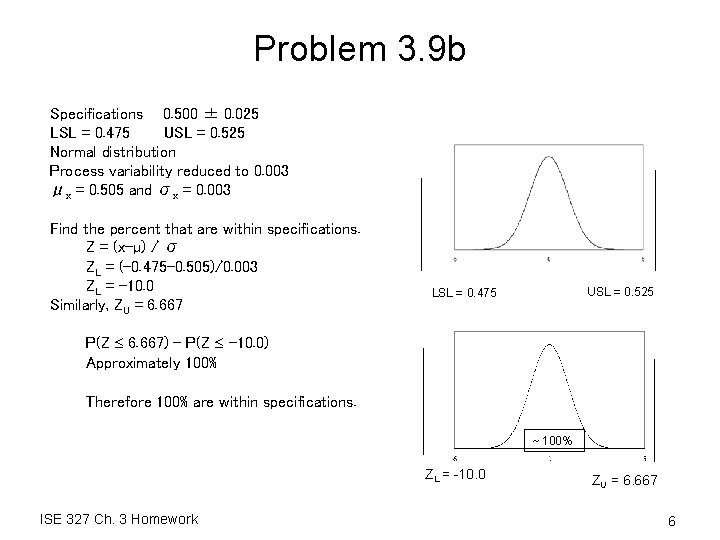
Problem 3. 9 b Specifications 0. 500 ± 0. 025 LSL = 0. 475 USL = 0. 525 Normal distribution Process variability reduced to 0. 003 μx = 0. 505 and σx = 0. 003 Find the percent that are within specifications. Z = (x-µ) / σ ZL = (-0. 475 -0. 505)/0. 003 ZL = -10. 0 Similarly, ZU = 6. 667 USL = 0. 525 LSL = 0. 475 P(Z 6. 667) - P(Z -10. 0) Approximately 100% Therefore 100% are within specifications. ~ 100% ZL = -10. 0 ISE 327 Ch. 3 Homework ZU = 6. 667 6