Using the Quadratic Formula to Solve a Quadratic

Using the Quadratic Formula to Solve a Quadratic Equation

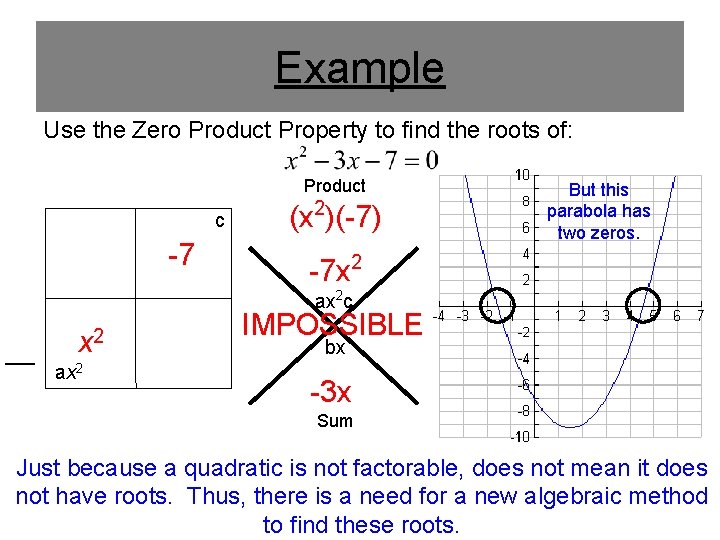
Example Use the Zero Product Property to find the roots of: Product c -7 (x 2)(-7) But this parabola has two zeros. -7 x 2 ax 2 c ___ x 2 ax 2 IMPOSSIBLE bx -3 x Sum Just because a quadratic is not factorable, does not mean it does not have roots. Thus, there is a need for a new algebraic method to find these roots.

Quadratic Formula For ANY 0 = ax 2 + bx +c (standard form) the value(s) of x is given by: MUST equal 0 Plus or Minus Opposite of b “All Over”

Solving a Quadratic with the Quadratic Formula Algebraically solve: Must equal 0 Find the values of “a, ” “b, ” “c” a = 1 b = -3 c = -7 Substitute into the Quadratic Formula Or you can write two expressions. One with addition in the numerator and other with subtraction. This is also an EXACT answer. Simplify the expression in the square root first Since the square root can not simplified, this is an acceptable EXACT answer Or you can approximate the expressions (don’t forget parentheses). This is NOT exact.

Solving a Quadratic with the Quadratic Formula Algebraically solve: Must equal 0 Find the values of “a, ” “b, ” “c” a = 2 b = 6 c = -5 Substitute into the Quadratic Formula The GCF of every term is 2 Simplify the expression in the square root first The square root can be simplified.

Solving a Quadratic: Make Sure to Isolate 0 Solve: Find the values of “a, ” “b, ” “c” Solve for 0 first! a=1 b = -3 c = -4 Distribute Substitute into the Quadratic Formula Since the answers will be rational, it is best to list both. Simplify the expression in the square root first Or The square root can be simplified.

Solving a Quadratic with the Quadratic Formula: Two Solutions Algebraically solve: Must equal 0 Find the values of “a, ” “b, ” “c” a = 4 b = 0 c = -121 Substitute into the Quadratic Formula Since the answers will be rational, it is best to list both. Simplify the expression in the square root first Or The square root can be simplified.

Solving a Quadratic with the Quadratic Formula: No Solutions Algebraically solve: Find the values of “a, ” “b, ” “c” Must equal 0 a = 1 b = -5 c = 9 Substitute into the Quadratic Formula The graph of the quadratic has no x-intercepts. Simplify the expression in the square root first This can not be calculated because you can not square root a negative. NO SOLUTIONS

Solving a Quadratic with the Quadratic Formula: One Solution Algebraically solve: Must equal 0 Find the values of “a, ” “b, ” “c” a = 36 b = -60 c = 25 Substitute into the Quadratic Formula The is no difference to adding zero or subtracting 0. This expression will result in only one answer. Simplify the expression in the square root first The square root of 0 is 0.

The Discriminant of a Quadratic For ANY 0 = ax 2 + bx +c (standard form) the value given by: If the Discriminant (the value underneath the square root in the quadratic formula) is…. • Greater than zero there are two roots • Equal to zero there is one root • Less than zero there are no roots