Using the Normal Distribution Using the Normal Distribution

Using the Normal Distribution

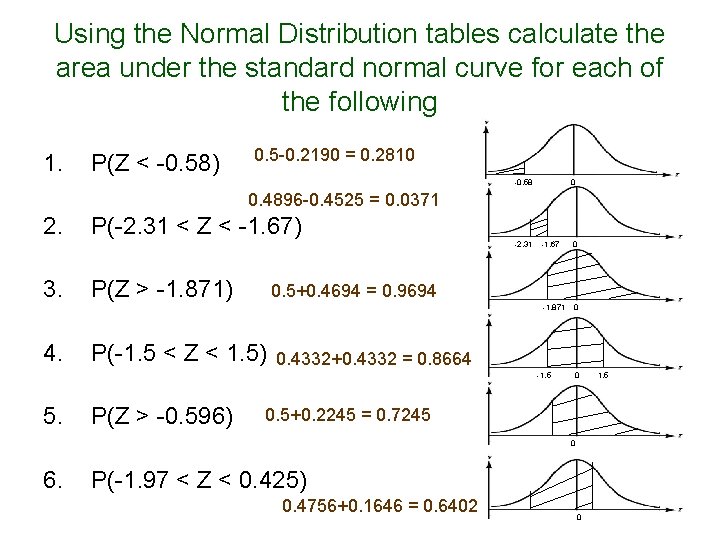
Using the Normal Distribution tables calculate the area under the standard normal curve for each of the following 1. P(Z < -0. 58) 0. 5 -0. 2190 = 0. 2810 -0. 58 0 0. 4896 -0. 4525 = 0. 0371 2. P(-2. 31 < Z < -1. 67) -2. 31 3. P(Z > -1. 871) 4. P(-1. 5 < Z < 1. 5) -1. 67 0 -1. 871 0 0. 5+0. 4694 = 0. 9694 0. 4332+0. 4332 = 0. 8664 -1. 5 5. P(Z > -0. 596) 0 0. 5+0. 2245 = 0. 7245 0 6. P(-1. 97 < Z < 0. 425) 0. 4756+0. 1646 = 0. 6402 0 1. 5

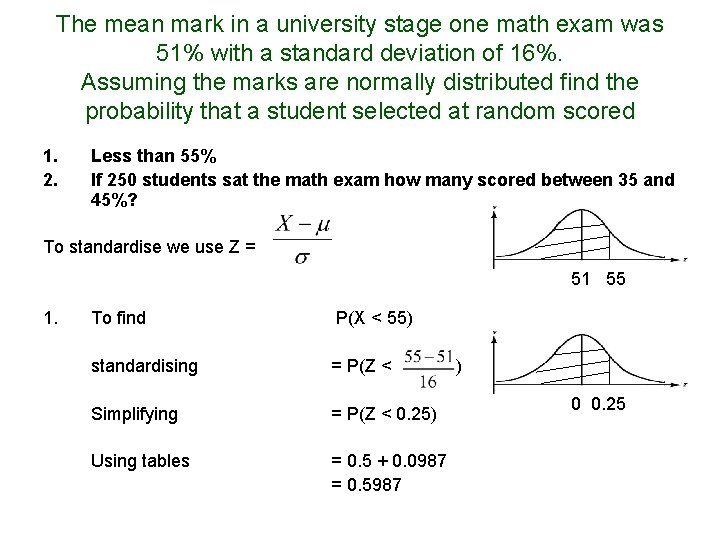
The mean mark in a university stage one math exam was 51% with a standard deviation of 16%. Assuming the marks are normally distributed find the probability that a student selected at random scored 1. 2. Less than 55% If 250 students sat the math exam how many scored between 35 and 45%? To standardise we use Z = 51 55 1. To find P(X < 55) standardising = P(Z < Simplifying = P(Z < 0. 25) Using tables = 0. 5 + 0. 0987 = 0. 5987 ) 0 0. 25

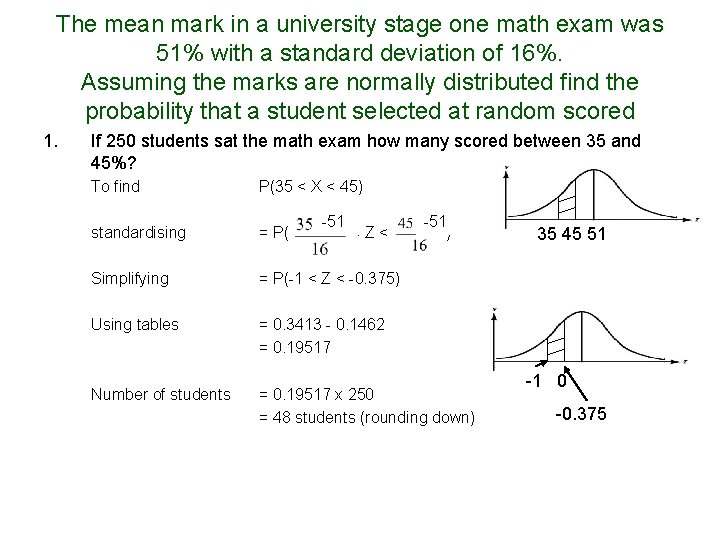
The mean mark in a university stage one math exam was 51% with a standard deviation of 16%. Assuming the marks are normally distributed find the probability that a student selected at random scored 1. If 250 students sat the math exam how many scored between 35 and 45%? To find P(35 < X < 45) standardising = P( Simplifying = P(-1 < Z < -0. 375) Using tables = 0. 3413 - 0. 1462 = 0. 19517 Number of students = 0. 19517 x 250 = 48 students (rounding down) -51 <Z< -51 ) 35 45 51 -1 0 -0. 375