Using the Metric System A Why do scientists




















- Slides: 21

Using the Metric System A. Why do scientists use the metric system? � The metric system was developed in France in 1795 - used in all scientific work because it has been recognized as the world wide system of measurement since 1960. � SI system is from the French for Le Systeme International d’Unites. � The metric system is used in all scientific work because it is easy to use. The metric system is based upon multiples of ten. Conversions are made by simply moving the decimal point.

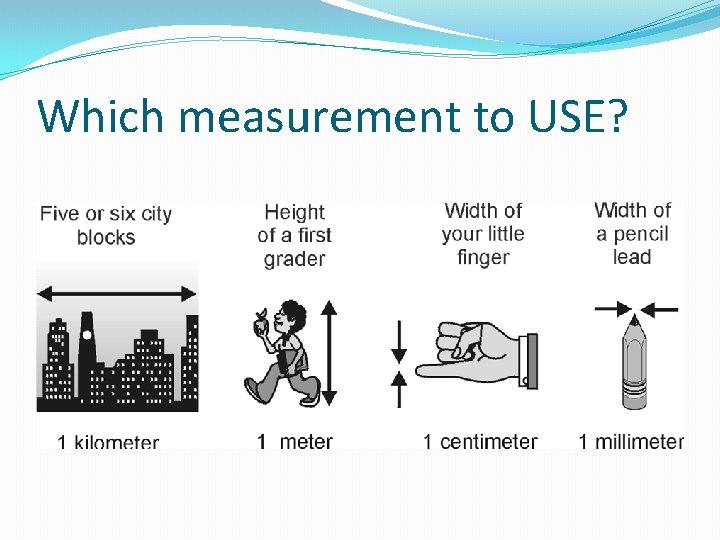
What is the basic unit of length? �The meter – a little longer than a yard

What do scientists use to measure the length of an object smaller than a yard? �A centimeter – one hundredth of a meter, so there are 100 centimeters in a meter �A millimeter – There are 1, 000 millimeters in a meter

How do scientists measure long distances? �The kilometer – There are 1, 000 meters in a kilometer

Which measurement to USE?

Base Units (Fundamental Units) QUANTITY NAME SYMBOL ________________________ Length meter m --------------------------------------Mass gram g ---------------------------------------Time second s ---------------------------------------Temperature Kelvin k ----------------------------------------Volume(liquid)_____liter_______L________

SI Prefixes Prefix Symbol Multiplication Factor Term Micro u (0. 000 001) one millionth Milli m (0. 001) one thousandth Centi c (0. 01) one hundredth Deci d (0. 1) one tenth One Unit Deka dk Hecto h Kilo k Mega M 1 10 1000 1 000 one ten one hundred one thousand one million

Metric Units Used In This Class QUANTITY Length NAME meter centimeter millimeter kilometer SYMBOL m cm mm km Mass gram kilogram centigram milligram g kg cg mg Volume liter (liquid) milliliter (liquid) cubic centimeter (solid) L (l) m. L (ml) cm 3

Derived Units �Base Units – independent of other units-measure �Derived Units – combination of base units-calculated Examples � density g/L mass / volume (grams per liter) �volume m x m = meters cubed �Velocity m/s (meters per second

SCIENTIFIC NOTATION Scientific Notation: Easy way to express very large or small numbers � A. 0 x � � � 10 x A – number with one non-zero digit before decimal x -exponent- whole number that expresses the number decimal places � if x is (-) then it is a smaller -left � if x is (+) than it is larger-right

PRACTICE �Convert to Normal � 2. 3 x 1023 m 3. 4 x 10 -5 cm Convert to SN 3, 400, 000, . 0000000456

Multiplying �Calculating in Scientific notation �Multiplying� Multiple the numbers � Add the exponents �(2. 0 x 104) (4. 0 x 103) = 8. 0 x 107

Dividing � divide the numbers � subtract the denominator exponent from the numerator exponent � 9. 0 x 107 � 3. 0 x 105 3. 0 x 102

Add �Add or subtract � get the exponents of all # to be the same � calculate as stated � make sure the final answer is in correct scientific notation form � 7. 0 x 10 4 + 3. 0 x 10 3 = � 7. 0 x 104 +. 3 x 104 = 7. 3 x 104 � 70, 000 + 3, 000 = 73000= 7. 3 x 10 4

subtract � 7. 0 x 10 4 - 3. 0 x 10 3 = � 7. 0 x 104 –. 30 x 104 = 6. 7 x 104 � 70, 000 - 3 000 =67, 000

PRACTICE �Add: � 2. 3 x 103 cm + 3. 4 x 105 cm �Subtract: � 2. 3 x 103 cm - 3. 4 x 105 cm �Multiply: �: 2. 3 x 103 cm X 3. 4 x 105 cm � �Divide: �: 2. 3 x 103 cm / 3. 4 x 105 cm �

Making Unit Conversions � Make conversions by moving the decimal point to the left or the right using: “ king henry died unit drinking chocolate milk” Examples 1. 10. 0 cm = _____m 2. 34. 5 m. L = _____L 3. 28. 7 mg = _____kg

Factor label method / Dimensional analysis Use equalities to problem solve converting units. quantity desired = quantity given x conversion factor (equality) �A-given unit �B-desired unit �C-given unit �A x B � C must equal 1 use equality sheet � �

Equalities You Need To Know 1 km = 1000 m 1 m = 100 cm 1 m = 1000 mm 1 L = 1000 m. L 1 kg = 1000 g 1 g = 100 cg 1 g = 1000 mg

ENGLISH TO METRIC � 1 inch=2. 5 centimeters � 1 gal=3. 8 liters � 1 lb= 4. 4 Newtons � 1 qt =. 94 Liters � 1 ft =. 30 meters � 12 in =. 30 meters � 1 mi = 1. 6 Km

Four-step approach When using the Factor-Label Method it is helpful to follow a four-step approach in solving problems: 1. What is question – How many sec in 56 min 2. What are the equalities- 1 min = 60 sec 3. Set up problem (bridges) 56 min 60 sec 1 min 4. Solve the math problem -multiple everything on top and bottom then divide 56 x 60 / 1