USING THE DERIVATIVE st Differentiation st Lesson Section

USING THE DERIVATIVE s(t) Differentiation s’’(t)

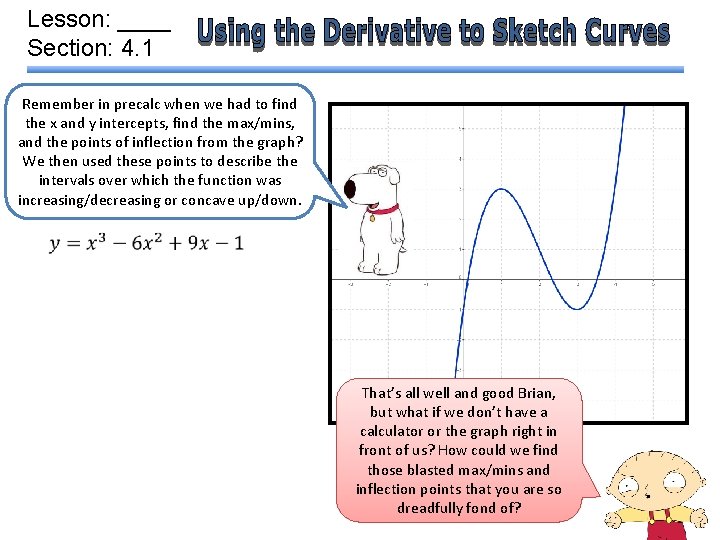
Lesson: ____ Section: 4. 1 Remember in precalc when we had to find the x and y intercepts, find the max/mins, and the points of inflection from the graph? We then used these points to describe the intervals over which the function was increasing/decreasing or concave up/down. That’s all well and good Brian, but what if we don’t have a calculator or the graph right in front of us? How could we find those blasted max/mins and inflection points that you are so dreadfully fond of?

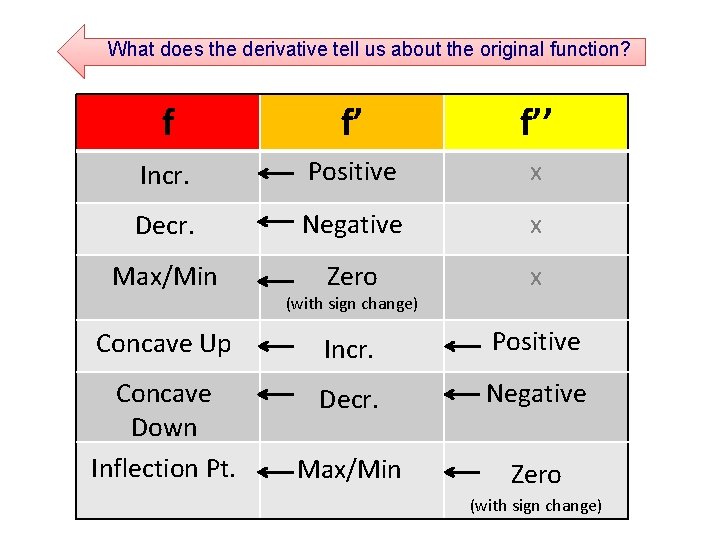
What does the derivative tell us about the original function? f f’ f’’ Incr. Positive x Decr. Negative x Max/Min Zero x Concave Up Incr. Positive Concave Down Inflection Pt. Decr. Negative Max/Min Zero (with sign change)

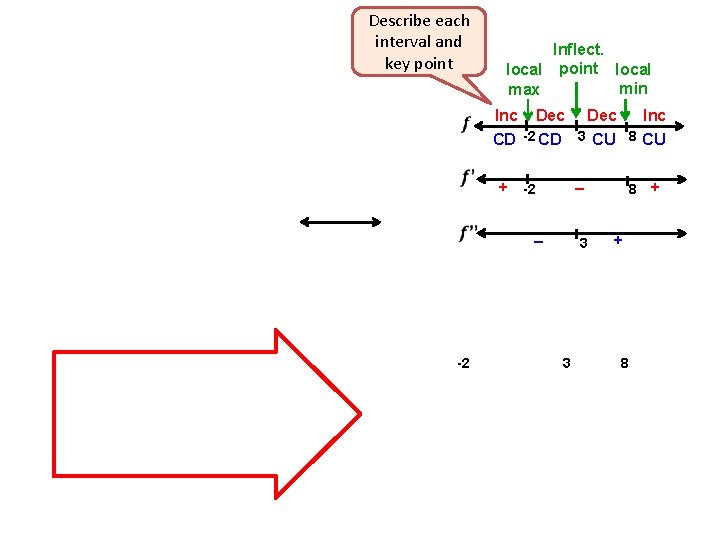
Describe each interval and key point Inflect. local point local min max Inc Dec Inc CD -2 CD 3 CU 8 CU + -2 – – -2 3 3 8 +

THE FIRST DERIVATIVE TEST FOR LOCAL EXTREMA local min – local min + local max + –

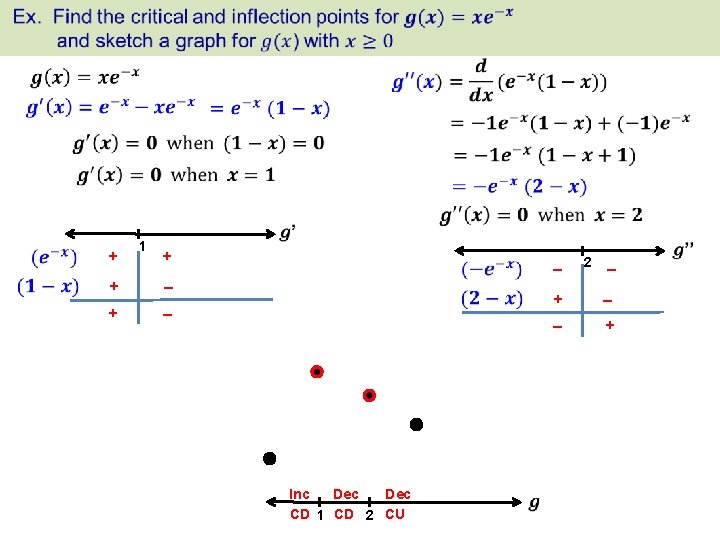
THE SECOND DERIVATIVE TEST FOR LOCAL EXTREMA LOCAL MINIMUM Concave up! LOCAL MAXIMUM Concave down! This is awesome! No need for test intervals! Just plug your critical number into the second derivative and see if it’s + or – ! However, it’s only useful if finding the second derivative is easy (like polynomials) INFLECTION POINTS A point at which the graph of a function changes concavity is called an inflection point of f. Think about it! An inflection point corresponds to a max/min on the derivative so this is really just an extension of our previous tests for extema!

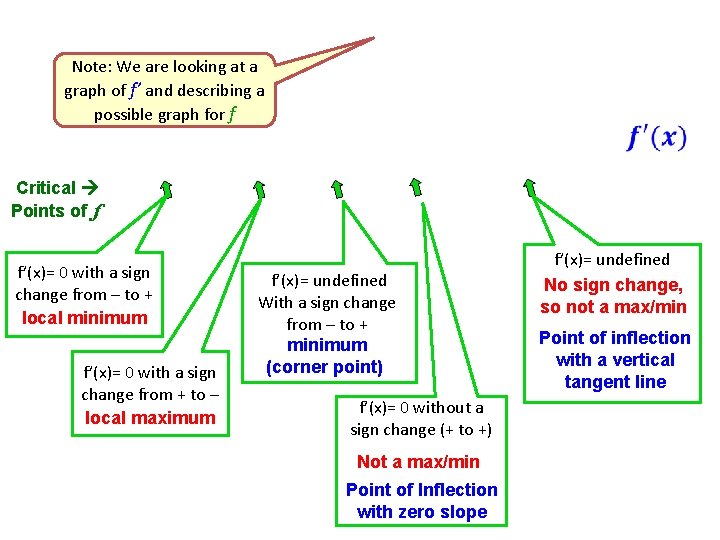
Note: We are looking at a graph of f’ and describing a possible graph for f Critical Points of f f’(x)= 0 with a sign change from – to + local minimum f’(x)= 0 with a sign change from + to – local maximum f’(x)= undefined With a sign change from – to + minimum (corner point) f’(x)= 0 without a sign change (+ to +) Not a max/min Point of Inflection with zero slope f’(x)= undefined No sign change, so not a max/min Point of inflection with a vertical tangent line

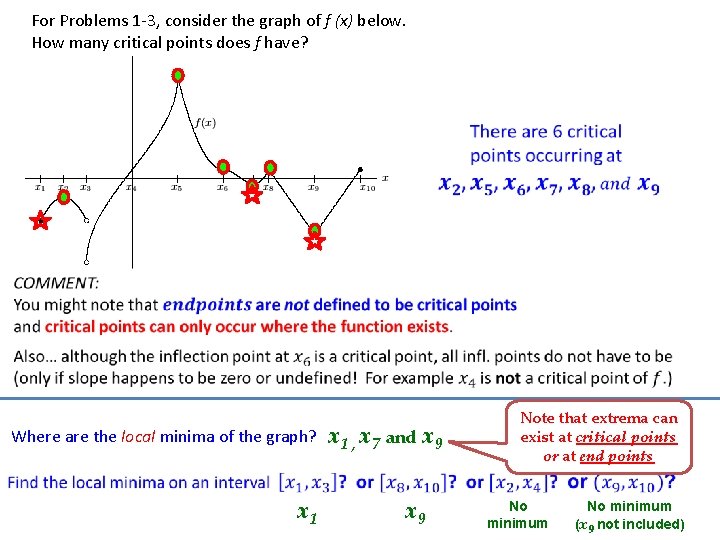
For Problems 1 -3, consider the graph of f (x) below. How many critical points does f have? Where are the local minima of the graph? x 1 , x 7 and x 9 Note that extrema can exist at critical points or at end points No minimum (x 9 not included)

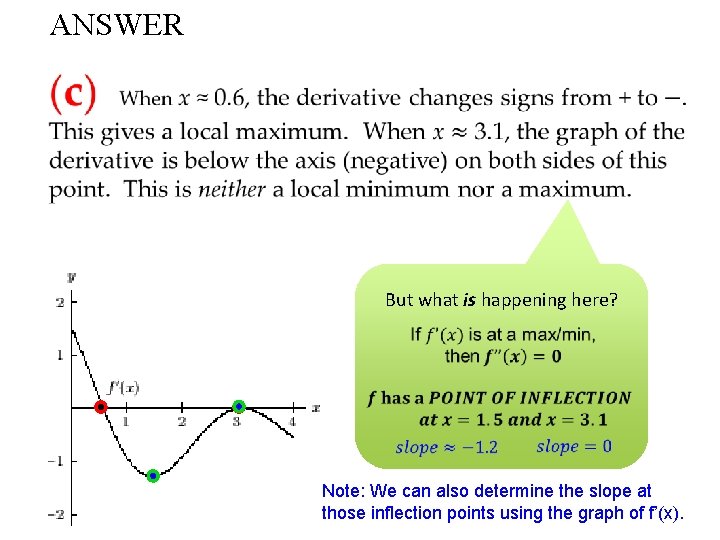
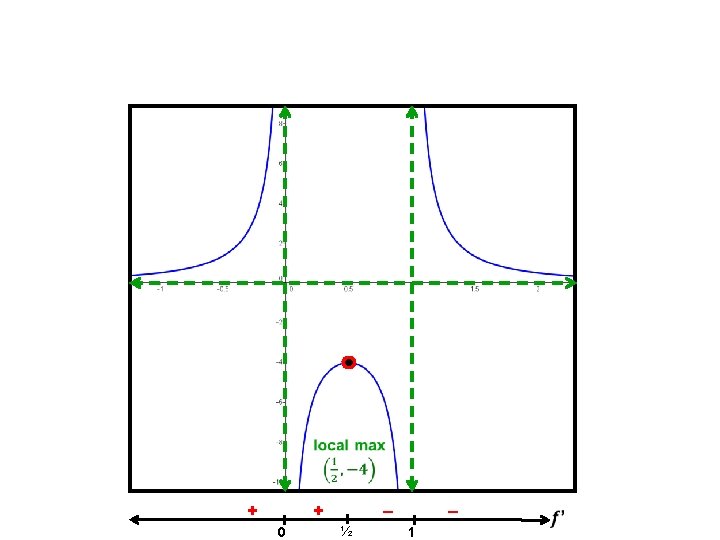
ANSWER But what is happening here? Note: We can also determine the slope at those inflection points using the graph of f’(x).

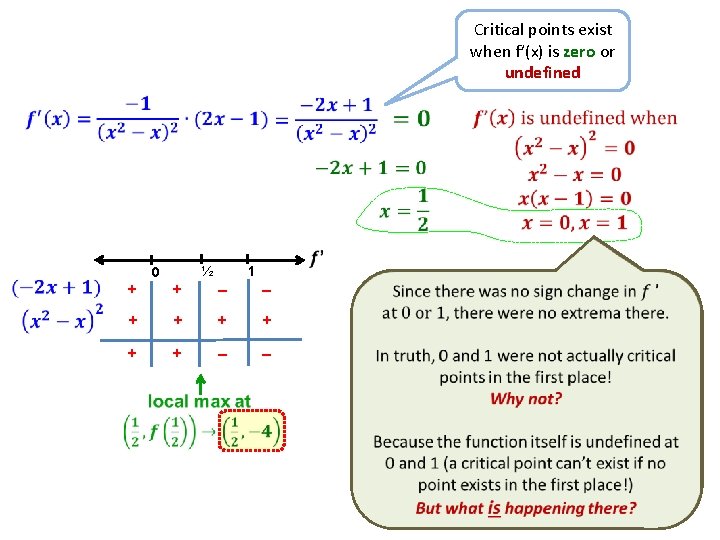
Critical points exist when f’(x) is zero or undefined 1 ½ 0 + + – – + + + – –

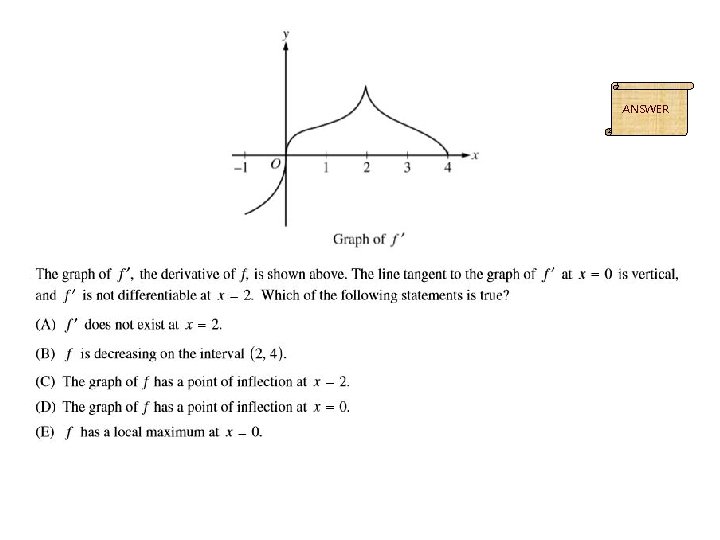
C ANSWER

C ANSWER B ANSWER