Using the Clicker If you have a clicker






























- Slides: 32

Using the “Clicker” If you have a clicker now, and did not do this last time, please enter your ID in your clicker. First, turn on your clicker by sliding the power switch, on the left, up. Next, store your student number in the clicker. You only have to do this once. Press the * button to enter the setup menu. Press the up arrow button to get to ID Press the big green arrow key Press the T button, then the up arrow to get a U Enter the rest of your BU ID. Press the big green arrow key.

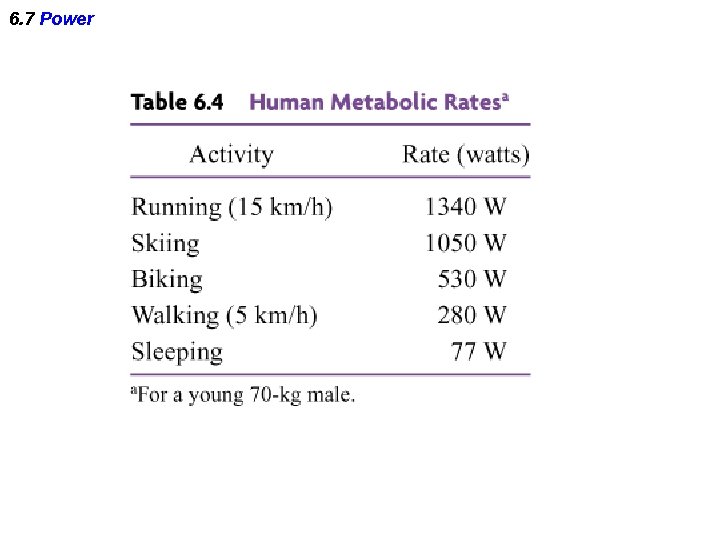
DEFINITION OF AVERAGE POWER Average power is the rate at which work is done, and it is obtained by dividing the work by the time required to perform the work.


Power of a human being An interesting calculation is the average power output of a human being. This can be determined from the amount of energy we consume in a day in the way of food. Most of us take in something like 2500 "calories" in a day, although what we call calories is really a kilocalorie. Use this as our energy output per day [Why is this a valid assumption? ]. Take the 2. 5 x 106 cal and convert to joules, using the conversion factor: 1 cal = 4. 186 J This gives roughly 1 x 107 J. Figuring out our average power output, we simply divide the energy by the number of seconds in a day, 86400, which gives a bit more than 100 W.

6. 7 Power

A ballistic pendulum is a device used to measure the speed of a bullet. A bullet of mass m is fired at a block of wood (mass M) hanging from a string. The bullet embeds itself in the block, and causes the combined block plus bullet system to swing up a height h. What is v 0, the speed of the bullet before it hits the block? Simulation of the ballistic pendulum We will work backwards to find an expression for v 0.

Mechanical energy conservation? Define the zero level for gravitational potential energy so both the bullet and the block have zero initial gravitational potential energy. Is it then correct to set the bullet’s kinetic energy before the collision to the bullet + block’s gravitational potential energy when the bullet + block reach their highest point after the collision? 1. Yes 2. No

Mechanical energy conservation? Mechanical energy is not conserved in the collision. A completely inelastic collision occurs, in which some (in fact, most!) of the mechanical energy is transformed into thermal energy when the bullet embeds itself in the block. Is anything conserved during the collision?

Mechanical energy conservation? Mechanical energy is not conserved in the collision. A completely inelastic collision occurs, in which some (in fact, most!) of the mechanical energy is transformed into thermal energy when the bullet embeds itself in the block. Is anything conserved during the collision? Yes, momentum is conserved over the small time period during which the collision occurs.

Mechanical energy conservation! Mechanical energy is conserved in the pendulum motion after the collision. Work backwards, starting with the swing of the pendulum just after the collision until it reaches its maximum height, h. Write out the five-term energy-conservation equation. Eliminate terms that are zero. Substitute expressions for these terms:

Mechanical energy conservation! Solve for the speed of the pendulum at its lowest point. We get the familiar expression: This is the final velocity of the system after the collision. In our collision analysis, then, we have:

Analyzing the collision Apply momentum conservation to the collision. Momentum beforehand = momentum afterwards Bring in our previous result: Solve for the speed of the bullet before the collision:

A numerical example If we use the following: Mass of the bullet: m = 30 grams Mass of the block: M = 870 grams Maximum height: h = 0. 74 m We find that:

How much mechanical energy is lost? Look at the ratio of the kinetic energy after the collision to the kinetic energy before the collision: From momentum conservation: In our numerical example, this ratio is 0. 033. 3. 3% of the mechanical energy remains. 96. 7% is lost!

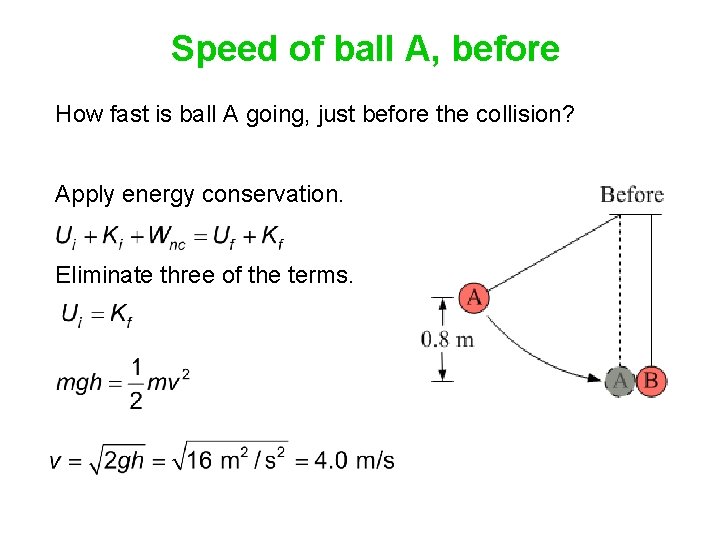
Worksheet, page 2 Two balls hang from strings of the same length. Ball A, with a mass of 4 kg, is swung back to a point 0. 8 m above its equilibrium position. Ball A is released from rest and swings down and hits ball B. After the collision ball A rebounds to a height of 0. 2 m above its equilibrium position, and ball B swings up to a height of 0. 05 m.

Speed of ball A, before How fast is ball A going, just before the collision? Apply energy conservation. Eliminate three of the terms.

Speed of the balls, after the collision We can use the same equation afterwards. For ball A afterwards: For ball B afterwards:

What is the mass of ball B? Find the mass of ball B. 1. 2. 3. 4. 5. 6. 4 kg 8 kg 12 kg 16 kg 24 kg None of the above

Find the mass of ball B Apply momentum conservation. How do we account for the fact that momentum is a vector?

Find the mass of ball B Apply momentum conservation. How do we account for the fact that momentum is a vector? Choose a positive direction (to the right), so the velocity of ball A after the collision is negative.

What kind of collision? Relative speed before the collision: 4 m/s Relative speed after the collision: 3 m/s Elasticity: . This is less than 1, so the collision is inelastic.

What kind of collision? Kinetic energy before the collision: 32 J Kinetic energy after the collision: 8 J + 12 J = 20 J The kinetic energy is smaller after the collision, so the collision is inelastic. It is not completely inelastic, because the two balls do not stick together after the collision.

Collisions in two dimensions The Law of Conservation of Momentum applies in two and three dimensions, too. To apply it in 2 -D, split the momentum into x and y components and keep them separate. Write out two conservation of momentum equations, one for the x direction and one for the y direction. For example: Simulation of a 2 -D collision

Baseball and basketball Dropping a basketball with a baseball balanced on top can produce interesting results. Watch the demonstration. The basketball has three times the mass of the baseball. How do we explain what we see? Let’s start by analyzing this as an elastic collision. Simulation of the baseball/basketball situation

Baseball and basketball The two balls drop through the same height h, so they are both traveling down with a speed v when the basketball hits the ground. Assumption: the basketball’s collision with the floor is elastic, so after colliding with the floor the basketball’s velocity is v directed up.

Baseball and basketball Now we have a collision between the baseball, of mass m and velocity v down, and the basketball, of mass 3 m and velocity v up. Observation: What does the basketball do after the collision?

Baseball and basketball Now we have a collision between the baseball, of mass m and velocity v down, and the basketball, of mass 3 m and velocity v up. Observation: What does the basketball do after the collision? The basketball is essentially at rest after the collision. Apply momentum conservation to find the speed of the baseball. Choose up to be positive. vf = ?

Baseball and basketball Now we have a collision between the baseball, of mass m and velocity v down, and the basketball, of mass 3 m and velocity v up. Observation: What does the basketball do after the collision? The basketball is essentially at rest after the collision. Apply momentum conservation to find the speed of the baseball. Choose up to be positive. vf = +2 v (this solution also conserves kinetic energy)

Baseball and basketball How high does the baseball go? When it was dropped from a height h, the baseball acquired a speed v: If the baseball is fired up with a speed 2 v, how high does it go?

Baseball and basketball How high does the baseball go? When it was dropped from a height h, the baseball acquired a speed v: If the baseball is fired up with a speed 2 v, how high does it go? H = 4 h. The baseball goes four times as high. It would go even higher, to 9 h, if it’s mass was negligible compared to the basketball’s mass.

Which collision? You are driving at high speed along a divided, multi-lane highway when you see your evil twin, driving an identical car, going the wrong way and coming directly toward you. You both slam on your brakes, but it's too late to stop and there is about to be a collision. At the last instant you spot a large, solid immovable object by the side of the road. Assume the speed when you collide is the same whether you hit your evil twin or the immovable object, and that your evil twin is going at the same speed you are. Either collision is a head-on collision. It is better for you (in terms of you surviving the crash) to: 1. Hit your evil twin 2. Hit the immovable object 3. Neither one - they're equivalent as far as you're concerned

Whiteboard