Using Simulated Annealing and Evolution Strategy scheduling capital

Using Simulated Annealing and Evolution Strategy scheduling capital products with complex product structure By: Dongping SONG Supervisors: Dr. Chris Hicks and Prof. Chris F. Earl Department of MMM Engineering University of Newcastle, Oct. , 2000.

Contents • • Introduction Problem formulation A discrete event-driven model Simulated Annealing Evolution Strategy Case studies Conclusions

Introduction Production scheduling -- the allocation of resources over time to perform a collection of tasks (Baker, 1974). Two important points in scheduling: Sequencing -- in which order to perform tasks on resources Timing -- when to start and complete tasks

Introduction • The importance of sequencing has been well recognised, because the optimal schedule can only be characterised by the sequences for performance measures such as mean flow-time, percentage of jobs tardy, mean tardiness, etc. • However, timing scheduling is necessary for performance measures such as earliness and tardiness costs, total discrepancy from the due dates, etc.

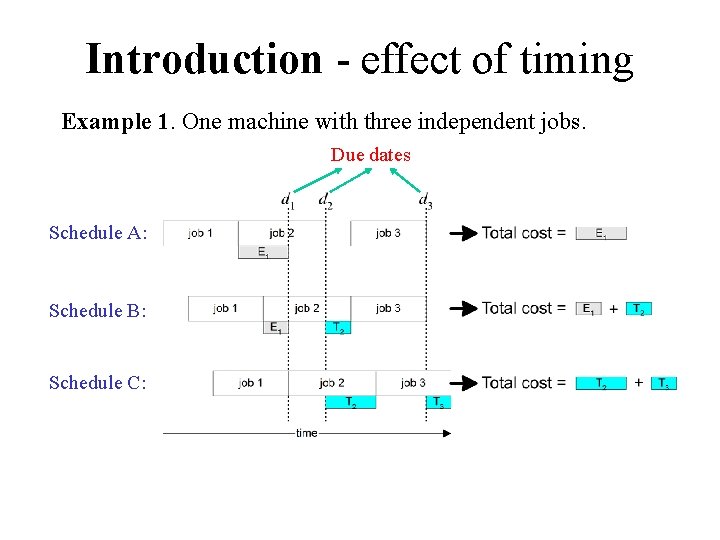
Introduction - effect of timing Example 1. One machine with three independent jobs. Due dates Schedule A: Schedule B: Schedule C:

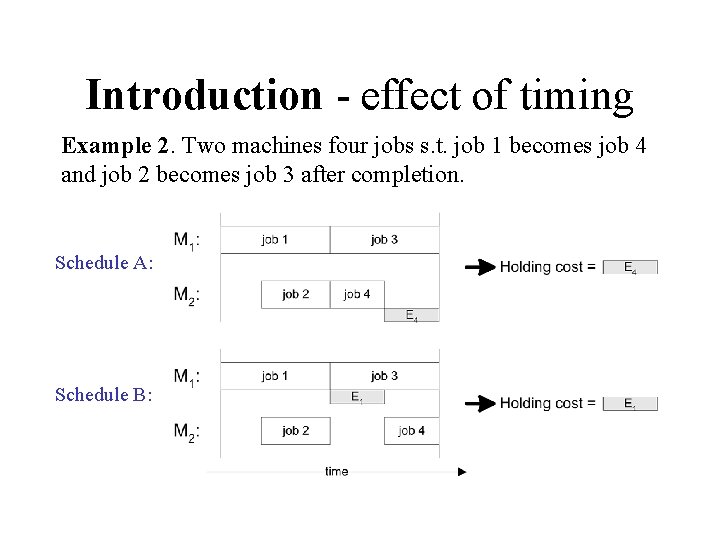
Introduction - effect of timing Example 2. Two machines four jobs s. t. job 1 becomes job 4 and job 2 becomes job 3 after completion. Schedule A: Schedule B:

Introduction - a capital product Complex product structure

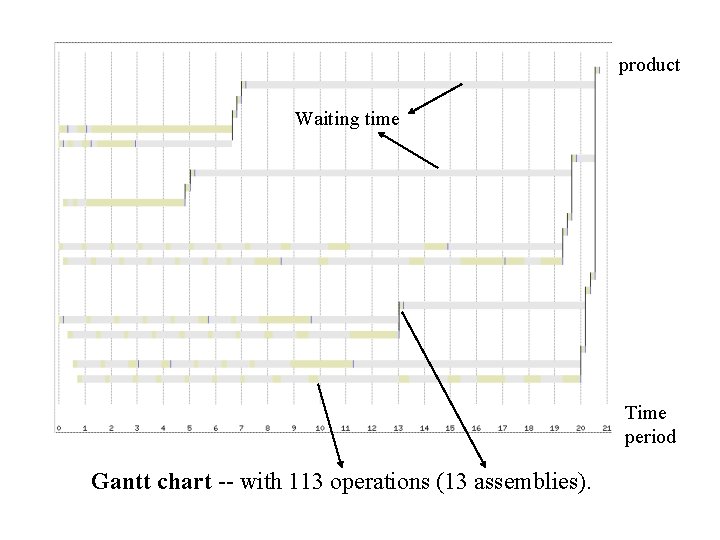
product Waiting time Time period Gantt chart -- with 113 operations (13 assemblies).

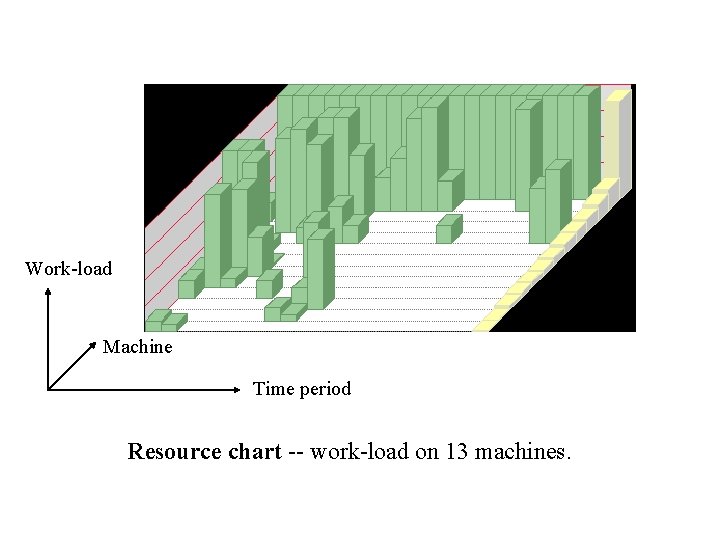
Work-load Machine Time period Resource chart -- work-load on 13 machines.

Introduction • Constraints in our scheduling problem: – Operation precedence constraints – Resource capacity constraints – Due date constraints – Assembly co-ordination requirements • Scheduling problem: to find optimal operation sequences and timings to meet above constraints and minimise total cost.

Problem formulation • Notation: si -- planned start time for operation i; N -- total operation number. • Solution space of schedules : = RN´{sequences on resources}. • Solution space can be simplified to RN, because operations on the same resource have different start times (i. e. timings imply sequences).

Problem formulation • The schedule problem can be formulated as a numerical optimisation problem. • Find the optimal {si, i=1, . . , N} to minimise the total cost J(s) = å (Work-in-progress holding costs + product earliness costs + product tardiness costs)

Problem formulation • Questions: (1) How to execute a schedule that is characterised by {si} ? (2) How to evaluate the cost function for a given schedule ?

Discrete event-driven model • Two types of events : – the start of an operation – the completion of an operation. • Two constraints to trigger the start events : – Physical constraints : an event cannot occur before all preceding events are completed. – Planning constraints : an operation cannot be started before its planned start time si.

Discrete event-driven model The evolution of the system for a given schedule {si} can be described by: • If a resource is idle, an operation will be processed as soon as the physical and planning constraints are satisfied. • If there is a queue of operations ready for processing, the operation with the earliest si will be processed first.

Simulated Annealing • Neighbourhood of a solution -- by adding a random number to each si. • Outer loop -- cooling the temperature T until T=0. • Inner loop -- perform Metropolis simulation with fixed T to find equilibrium state.

Simulated Annealing • Adjust the solution : – shift the whole schedule (optional) – impose precedence constraints (optional) – make non-negative • Evaluate cost function : – run the DED model

Simulated Annealing

Evolution Strategy • Similarity of Genetic Algorithms and ES: – model organic evolution. – iterative scheme including “selection”, “crossover” and “mutation”. • Difference of GA and ES: – GA uses binary or string representations, suitable for combinatorial optimisation problem. – ES uses continuous variable, suitable for numerical optimisation problem.

Evolution Strategy • Crossover -- randomly copy elements from parents column by column.

Evolution Strategy • Mutation -- add a random number from a Normal distribution to each element.

Evolution Strategy • Adjust the solution : – shift the whole schedule (optional) – impose precedence constraints (optional) – make non-negative • Evaluate cost function -- run the DED model. • Selection -- choose a set of best offspring as parents for the next generation

Evolution Strategy

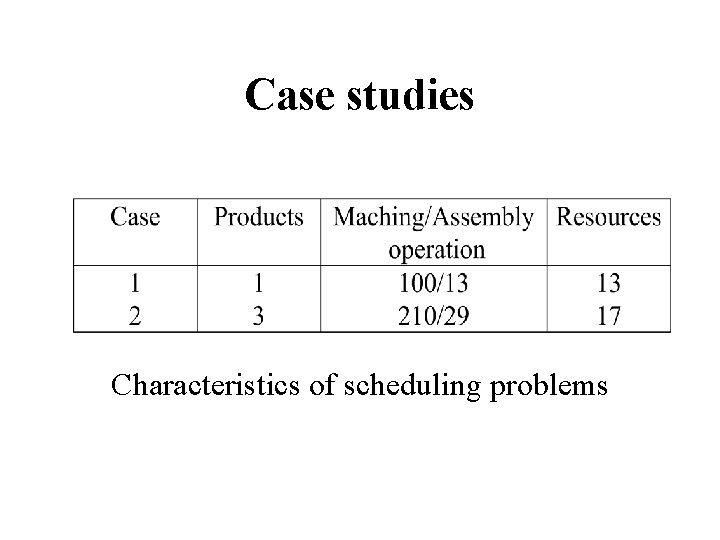
Case studies Characteristics of scheduling problems

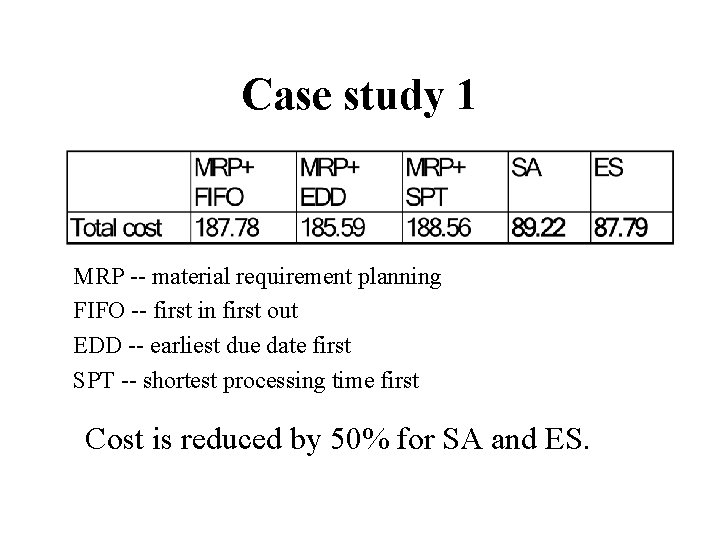
Case study 1 MRP -- material requirement planning FIFO -- first in first out EDD -- earliest due date first SPT -- shortest processing time first Cost is reduced by 50% for SA and ES.

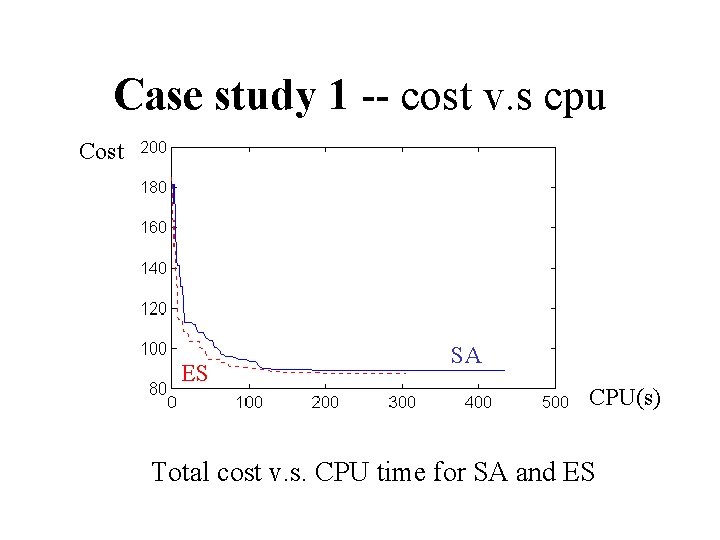
Case study 1 -- cost v. s cpu Cost ES SA CPU(s) Total cost v. s. CPU time for SA and ES

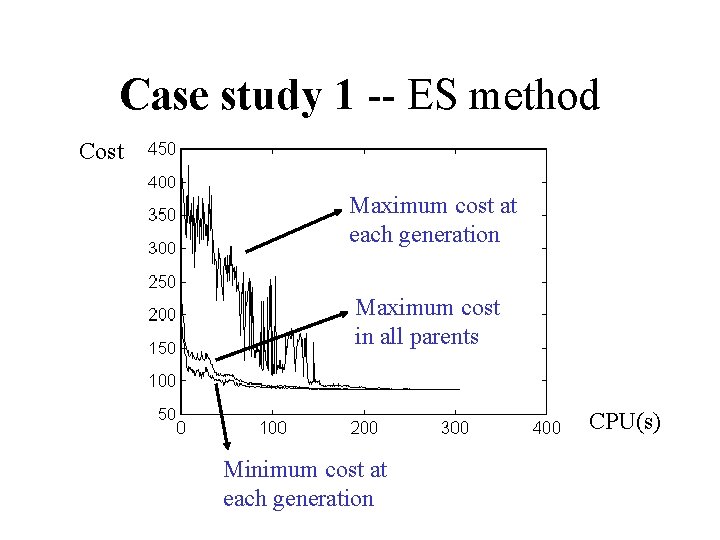
Case study 1 -- ES method Cost Maximum cost at each generation Maximum cost in all parents CPU(s) Minimum cost at each generation

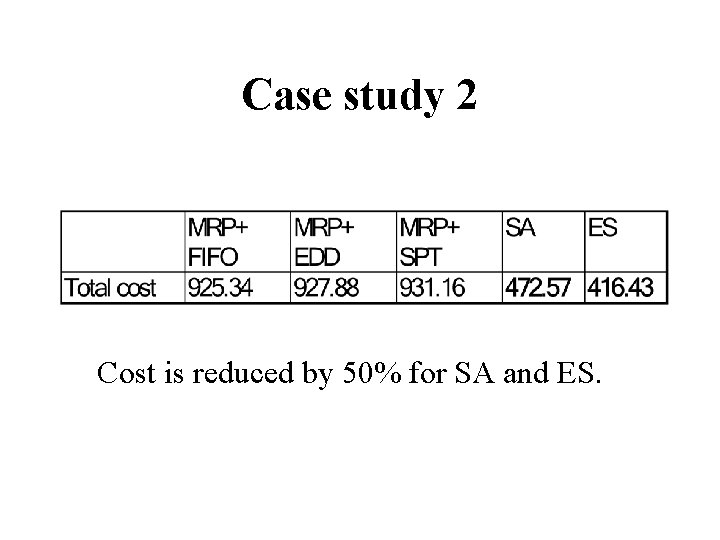
Case study 2 Cost is reduced by 50% for SA and ES.

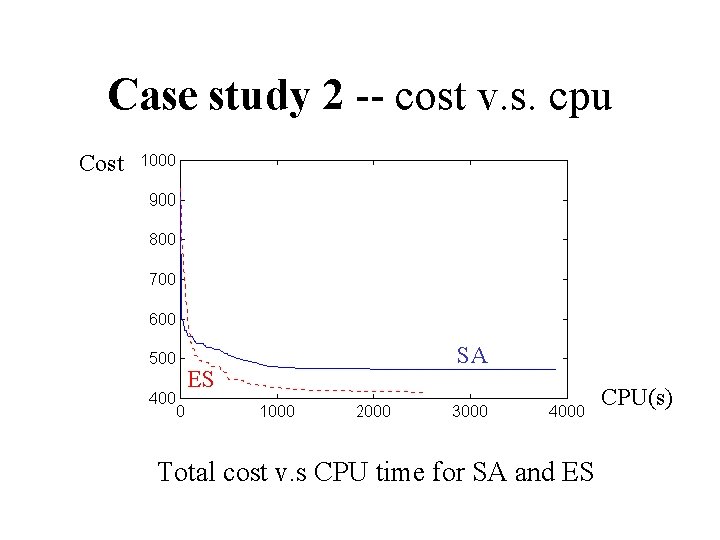
Case study 2 -- cost v. s. cpu Cost ES SA Total cost v. s CPU time for SA and ES CPU(s)

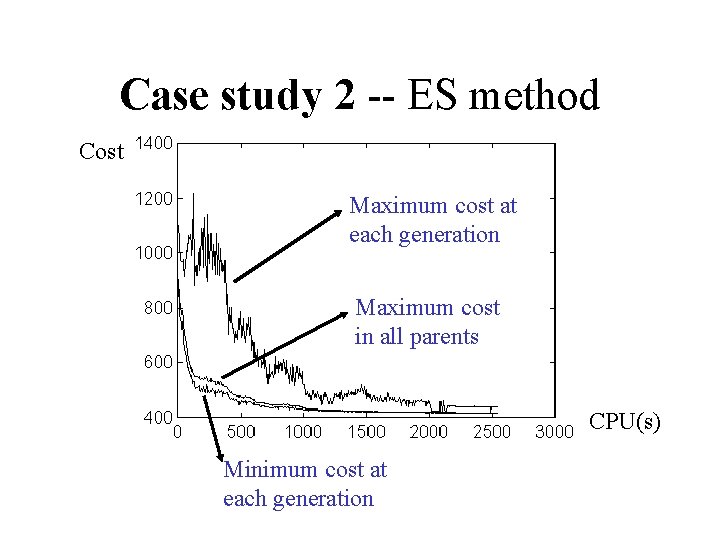
Case study 2 -- ES method Cost Maximum cost at each generation Maximum cost in all parents CPU(s) Minimum cost at each generation

Conclusions • SA and ES can reduce total cost by 50% compared with MRP+dispatching rules. • ES is generally better than SA in both cost and CPU time. • ES is more robust to its initial parameter selection than SA.

Conclusions • Suggestions for SA initial parameters: – T 0 and step-size is taken from [d/N, 20*d/N]; – Temperature cooling rate > 0. 5 and step-size reduction factors > 0. 70; – No-improvement number at inner loop > N/2; • Suggestions for ES initial parameters: – Offspring population is from [N/2, 2*N]; – Parent population is 1/10 to 1/5 of offspring; – Initial standard deviation is from [d/N, 5*d/N].

Further work • Compare our methods with GA (Pongcharoen, et al. ) for the same cost function. • Develop hybrid optimisation methods by combining SA, ES with Perturbation Analysis or heuristics. • Extend to stochastic situations such as dynamic customer demand arrivals and processing uncertainties.

SA -- effect of parameters T 0=1 T 0=40 T 0=20 T 0=10 Initial temperature and temperature cooling factor

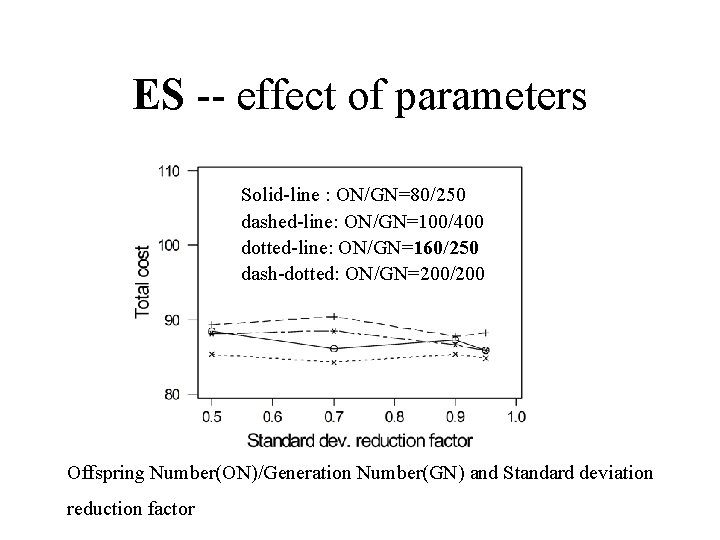
ES -- effect of parameters Solid-line : ON/GN=80/250 dashed-line: ON/GN=100/400 dotted-line: ON/GN=160/250 dash-dotted: ON/GN=200/200 Offspring Number(ON)/Generation Number(GN) and Standard deviation reduction factor