Using Sensor Data Effectively A major challenge in

Using Sensor Data Effectively • A major challenge in mobile robotics is accurate localisation. • Consider a robot with the following sensors: – Inertial Measurement Unit (IMU) – Camera – Wheel Encoders – Global Positioning • Each has different noise properties. Localization

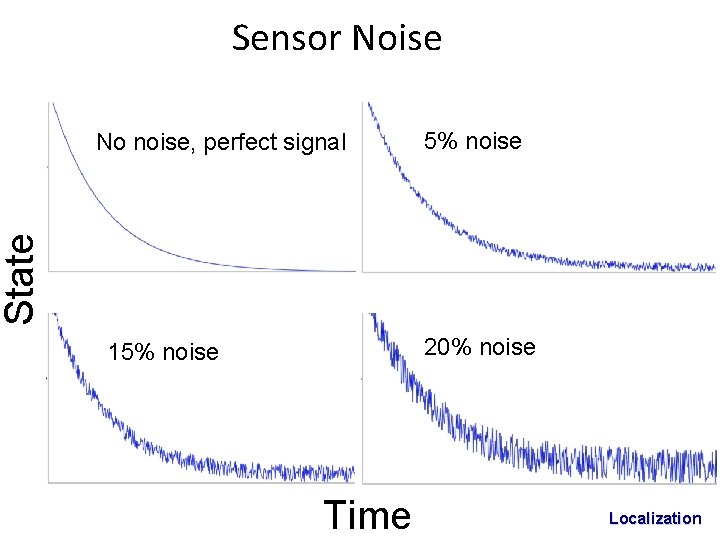
Sensor Noise 5% noise State No noise, perfect signal 20% noise 15% noise Time Localization

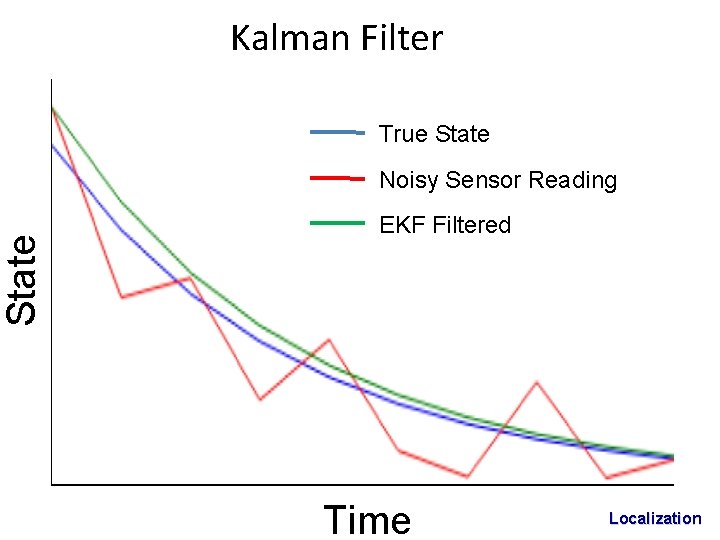
State Kalman Filter True State Noisy Sensor Reading EKF Filtered Time Localization

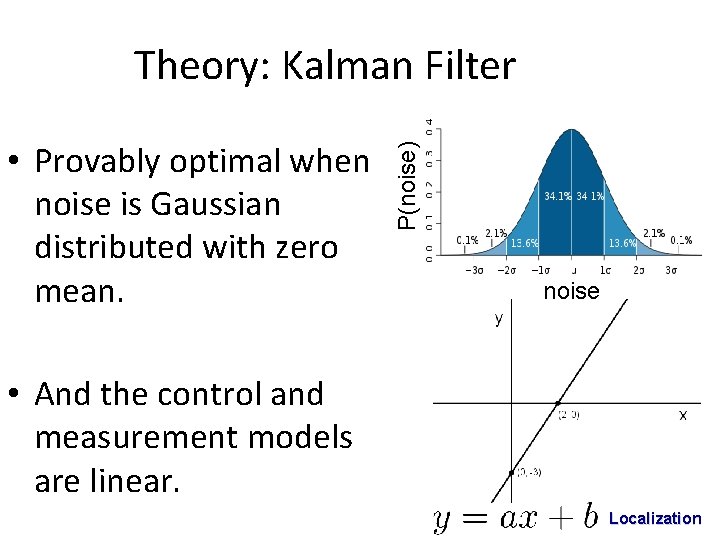
• Provably optimal when noise is Gaussian distributed with zero mean. P(noise) Theory: Kalman Filter noise • And the control and measurement models are linear. Localization

Linear Control and Observation Control (transition) Model: Observation Model: Localization

Relating Control, Measurement and Noise Localization

Relating Control, Measurement and Noise Localization

Extended Kalman Filter • The Kalman filter assumed linear relationships. • In real systems the relationship may be nonlinear. • But we can take the derivative of the signal to linearize it. • This is the extended Kalman filter. No longer optimal but works well. Localization

Sensor Fusion with Multiple States • Recall the sensor measurement is: • We would like to generalise this to multiple sensors with different kinds of states: – For example, states might be yaw-angle, velocity, or position. – Sensors might be IMU, encoders, or GPS. Localization

Sensor Fusion with Multiple States • Recall the sensor measurement is: • If we have three sensors with 2 different states we can write: With each row corresponding to a sensor and each column to a type of state. Localization

The EKF Algorithm Localization

Input previous state The EKF Algorithm estimate Localization

Input previous state The EKF Algorithm estimate Output an estimate for the current state Localization

Previous The EKF Algorithm covariance Localization

Previous The EKF Algorithm covariance … and the updated covariance matrix. Localization

Current The EKF Algorithm Observation Localization

The Kalman gain, , The EKF weights the. Algorithm sensor measurements according to, , the prediction covariance (noisiness). Localization

The EKF Algorithm The new observation coefficient matrix depends on how good the previous one was. Localization

The EKF Algorithm Prediction Step Localization

The EKF Algorithm Prediction Step Correction Step Localization

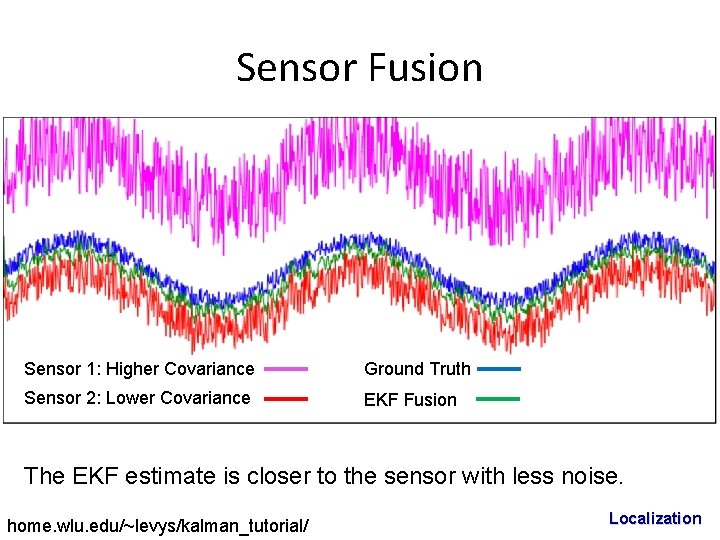
Sensor Fusion Sensor 1: Higher Covariance Ground Truth Sensor 2: Lower Covariance EKF Fusion The EKF estimate is closer to the sensor with less noise. home. wlu. edu/~levys/kalman_tutorial/ Localization

In Practice • The EKF is a recursive function that calls itself at each time step to improve the robot state estimate. • It weights sensor data by the variance they contribute to the state prediction. • ROS has an EKF package to do all this for us* *Moore, Thomas, and Daniel Stouch. 2016. “A Generalized Extended Kalman Filter Implementation for the Robot Operating System. ” In Intelligent Autonomous Localization Systems 13, 335– 48. Springer.

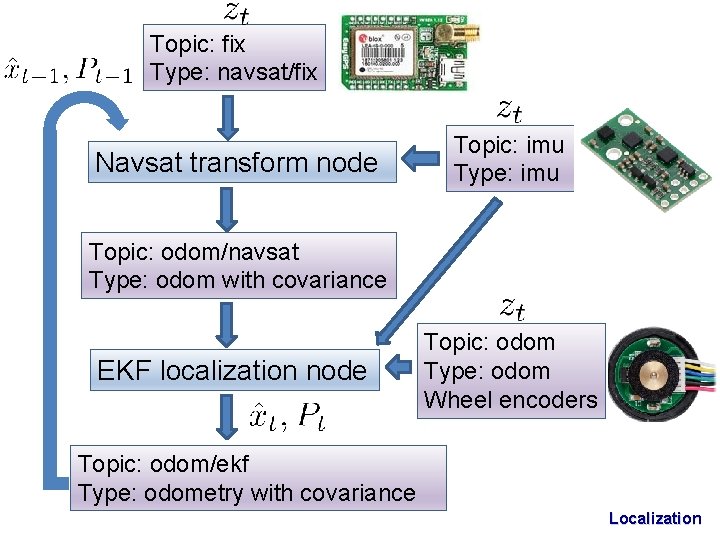
EKF in ROS • Two nodes: – ekf_localization: EKF implementation – Navsat node: sensor processing. Transforms latitude and longitude to the robots local frame. Localization

Topic: fix Type: navsat/fix Navsat transform node Topic: imu Type: imu Topic: odom/navsat Type: odom with covariance EKF localization node Topic: odom Type: odom Wheel encoders Topic: odom/ekf Type: odometry with covariance Localization

EKF Node Basic Configuration <rosparam="odom 0_config"> [true, false, x, y, z false, roll, pitch, yaw false, y velocity, z velocity false, true, roll velocity, pitch velocity, yaw velocity false, false] x accel. , y accel. , z accel. </rosparam> <rosparam="imu 0_config"> [false, false, true, true, true] </rosparam> In ~/rover_workspace/launch/rover_name. launch Localization

EKF Node Basic Configuration Localization

EKF Node Basic Configuration Has to be tuned through experiment. Localization

In Practice • Can set initial values for, , the prediction covariance matrix. • Small initial values tell the Robot that the sensor has low noise. • High values say that the sensor is noisy. • Ideally the covariance is measured experimentally for each sensor. • The initial value for can be the first sensor value. That is. Localization