USING SCIENTIFIC MEASUREMENTS SIGNIFICANT FIGURES Significant Figures Consist

USING SCIENTIFIC MEASUREMENTS

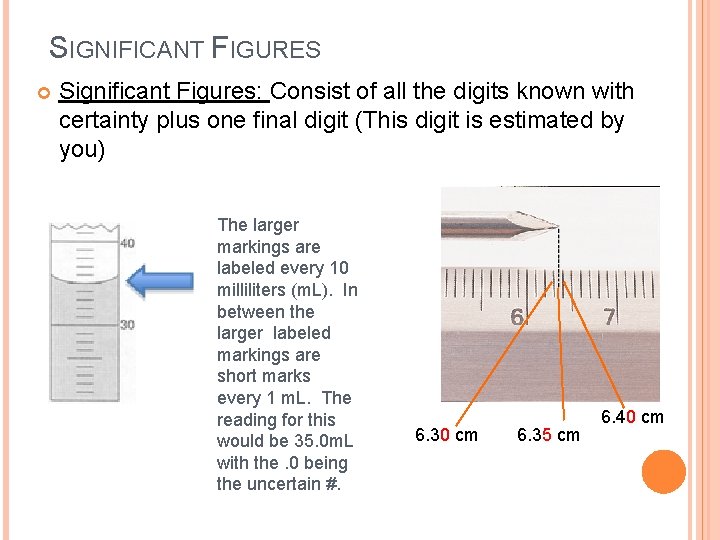
SIGNIFICANT FIGURES Significant Figures: Consist of all the digits known with certainty plus one final digit (This digit is estimated by you) The larger markings are labeled every 10 milliliters (m. L). In between the larger labeled markings are short marks every 1 m. L. The reading for this would be 35. 0 m. L with the. 0 being the uncertain #. 6. 30 cm 6. 35 cm 6. 40 cm

READING MEASUREMENTS FOR SIG FIGS • When reading an Electric Scale there is no need to add on a number. All numbers available are to be used and considered significant.

RULES FOR DETERMINING SIG FIGS � 1) ALL numbers that aren’t zero (1, 2, 3, 4, 5, 6, 7, 8, 9) are significant. Ex-83765 (5) � 2) ALL zeroes between non-zero numbers are significant. Ex- 404 (3) � 3) ALL zeroes which are at the end of a number and to the right of the decimal point are significant. Ex 1. 5600 (5) � 4) Zeros appearing in front of all non-zero digits are NOT significant. Ex-0. 0012 (2) 10. 0090 (6) � 5)Zeros at the end of a number but to the left of a decimal point are significant only if a decimal point has been placed to the right of that zero. If there is no decimal point then they are NOT significant. Ex-5000 (1) 5000. (4) 750 (2)

ROUNDING RULES Find the number you want to keep and look at the next number: If it is…. . Examples: (rounded to 3 sig figs) Greater than 5, increase the last digit by 1. Less than 5, do not change the last digit. 56. 87 g …. . 56. 9 g 12. 02 L …. 12. 0 L Equal to 5, followed by a number other than zero, increase the last digit by 1. 3. 7851 s …. 3. 79 s Equal to 5, followed by nothing or a zero If the number you are keeping is odd, increase the odd digit by 1. 2. 835 m …. 2. 84 m (because 3 is odd) Equal to 5, followed by nothing or a zero If the number you are keeping is even, do not change the even digit. 2. 645 m. L …. 2. 64 m. L (because 4 is even)

SIG FIG PRACTICE Determine the number of Sig Figs 4932. 20 cm 0. 0400 L 804. 5 g 0. 0144030 km 1002 m 400 m. L 30000. cm 0. 0000625000 kg Suppose the value “seven thousand cm” is reported to you. How would it be expressed if: You wanted to indicate 1 Sig Fig � You wanted to indicate 4 Sig Figs � You wanted to indicate 6 Sig Figs �

SIGNIFICANT FIGURES Addition and Subtraction Rules The answer must be rounded so that it contains the same number of digits to the right of the decimal point as there are in the measurement with the smallest number of digits to the right of the decimal point. � Ex. 2. 89 m + 0. 00043 m = 2. 89 m Multiplication Rules The product or quotient should be rounded off to the same number of significant figures as in the measurement with the fewest significant figures. � Ex. 3. 5293 mol x 34. 2 g/mol = 120. 70206 g = 121 g Conversion Factors and Sig Figs: Conversion Factors do not affect the amount of Sig Figs because they are exact. This means there is no error in them.

Scientific Notation: A method of writing very large and very small quantities as a number times 10 to a power : M x 10 n (Example-1404 = 1. 404 x 103) Keep all sig figs unless told otherwise.

SCIENTIFIC NOTATION 1. 2. 3. 4. 5. Find the decimal 569000. 00 Move (or jump) the decimal until you have one digit to the left of the decimal 569000. 00 Count the # of jumps (jumped left # is pos, jumped right # is neg) pos neg 569000. 00 Rewrite the number with the decimal in the new place and attach x 10 5. 69 x 10 Add the number of jumps as an exponent on the x 10 5. 69 x 105

Quantity-Anything that is measurable (has magnitude, size, or amount) ex- length, time, volume, mass…. . etc. Measurement-Represents a quantity with a # and unit SI Base Units: The International System of Units 1 -Length- l 2 -Mass- m meter-m kilogram-kg 3 -Time- t 4 -Temperature- T 5 -Amount of Substance-n seconds-s Kelvin-K mole-mol

CONVERTING TEMPERATURE Ko= Co + 273. 15 Fo = 9/5 (Co+32) Co = 5/9(Fo-32) Convert the following to Kelvin 1) 0 o C ____ 2) -50 o C ____ 3) 90 o C ____ 4) -20 o C ____ Convert the following to Celsius 5) 100 o K ____ 6) 200 o K ____ 7) 273 o K ____ 8) 350 o K ____

UNITS CONTINUED Derived Units: Any combination of SI Base Units Density: g/cm 3 Weight-Measure of the gravitational pull on matter (measured with a Spring Scale) � Newtons=kg • m s 2

MASS (m) Mass is the amount of matter present. How much stuff is there? Mass and weight are not the same thing Why do they seem the same here on earth? Will a person’s mass change on the moon? Will a person’s weight change on the moon?

VOLUME (V) Volume is a measure of how much space an object takes up. Measure volume in 2 ways � Solid straight sided objects-metric: cm 3, mm 3, etc Lx. Wx. H=Volume � Liquids and odd shaped objects: m. L, L, k. L, c. L, etc Use Graduated Cylinder or use water displacement 1 m. L=1 cm 3

Density: The ratio of mass to volume �D=m/V �All substances have a very specific density. �Density graphs are Directly Proportional �What would have to change to make density vary? Density= 19. 32 g/cm 3 Gold Memorize: Water has a density of 1 g/m. L or 1 g/cm 3

Density Column 1 -Which Sample would be at the top of the column? 2 -Which sample would fall to the bottom of the column? DENSITY PRACTICE PROBLEMS Silver has a density of 10. 5 grams/cm 3 and gold has a density of 19. 3 g/cm 3. Which would have the greater mass, 5 cm 3 of silver or 5 cm 3 of gold? � Gold with 96. 5 g An irregularly shaped stone was lowered into a graduated cylinder holding a volume of water equal to 2 ml. The height of the water rose to 7 ml. If the mass of the stone was 25 g, what was its density? � Density=5 g/m. L

ACCURACY AND PRECISION Accuracy-The closeness of measurements to the correct or accepted value How close was your measured value to the accepted value? Precision-The closeness of a set of measurements of the same quantity made in the same way. � How reproducible are your measurements?

% ERROR % Error: This is used to find out how accurate a measurement or average measurement is. � (Subtract the accepted value from the measured value, divide by the accepted value) multiply by 100 measured-accepted x 100 = % Error accepted � Negative sign (-) means measured # was smaller � Positive sign (+) means measured # was bigger Ex. If the accepted Density of cork is. 24 g/cm 3 and you measured it to be. 26 g/cm 3 then the % error would be: . 26 g/cm 3 -. 24 g/cm 3 x 100 = 8. 3% . 24 g/cm 3

CONVERTING BETWEEN UNITS Dimensional Analysis: An equation used to solve a problem using units or labels. Also called the factor label method. � It is used to go from one unit to another. Conversion Factor: Relationship between the two units. � You must ask how much of one does it takes to equal the other? Equation: Conversion Factor Starting Amount finishing unit starting unit = Finishing Amount Example of conversion factor for dollars and quarters 4 quarters or 1 dollar 4 quarters Example of conversion factor for cm and m 100 cm or 1 m 100 cm

DIMENSIONAL ANALYSIS Draw a T bar (Magic Bridge) 2. Find out the starting amount and unit. Hint**It’s a number with a unit. Write it down in the upper left hand corner. 3. Now decide on the finishing unit. 4. Make 2 fractions out of the starting and finishing units. How much of one equals the other? 5. Pick the fraction that has the starting unit on the bottom and place it into your T bar on the right hand side. 6. Cancel out any units that will cancel. 7. Multiply the stuff on top and divide by the stuff on the bottom. 1 x 10 -9 1 x 10 -6 . 001 . 1 1 10 1000 1 x 106 1 x 109 G M k h da m d c m µ n L g 1.

PRACTICE 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 304. 90 dimes nickels 293 50 pennies quarters 654 cm 3 m. L 8. 90258 x 104 Fingers hands 6. 29 x 1010 sec hours 5. 43 x 103 hr weeks 45. 5 cm m 1. 540 kg µg 12. 4 d. L h. L 4. 5 x 10 -6 m dm 9. 21 kg mg. 054 x 103 Mm nm 12. 1 x 10 -9 1 x 10 -6 . 001 . 1 1 10 1000 1 x 10 6 1 x 109 G M k h da m d c m µ n L g

CONVERTING VOLUME AND AREA If you have a measurement that has a unit with an exponent: for example: m 2, cm 3 You must use the same number of conversion factors as there is in the exponent. � Example: for m 2 you would need to list the conversion factor twice � Example: for cm 3 you would need to list the conversion factor three times

CONVERTING UNITS OF VOLUME 1. 2. 3. 4. 5. 6. 7. 310 000 cm 3 of concrete in cubic meters 6. 5 m 2 of steel sheet in square centimeters 0. 035 m 3 of chlorine gas in cubic centimeters 0. 49 cm 2 of copper in square millimeters 1200 µm 2 of acetic acid solution in square decimeters 87. 5 mm 3 of actinium in cubic centimeters 250 000 cm 2 of polyethylene sheet in hm 2

EXAMPLES 1. 2. 3. 4. 5. Your Eupopean Hairdresser wants to cut your hair 8. 0 cm shorter. How many inches will he be cutting off? (2. 54 cm = 1 in) The SGC Football team needs another 550 cm for a 1 st down. How many yards is this? If Jules Vern expressed the title of his famous book, “Twenty Thousand Leagues Under the Sea” in feet, what would the title be? (1 mile = 5280 ft, 1 League = 3. 450 miles) A piece of wire is 1. 4 m long. How many 1. 5 cm pieces can be cut from this wire? You need a room that is at least 1. 350 x 10 -3 km 2 for the Junior/Senior Prom. Your Cafetorium is 133. 9 ft wide and 67. 02 ft long. Is the Cafetorium big enough?