Using Reduction for the Game of NIM Nim

Using Reduction for the Game of NIM

Nim At each turn, a player chooses one pile and removes some sticks. The player who takes the last stick wins. Problem: Is there a move that guarantees a win for the current player?

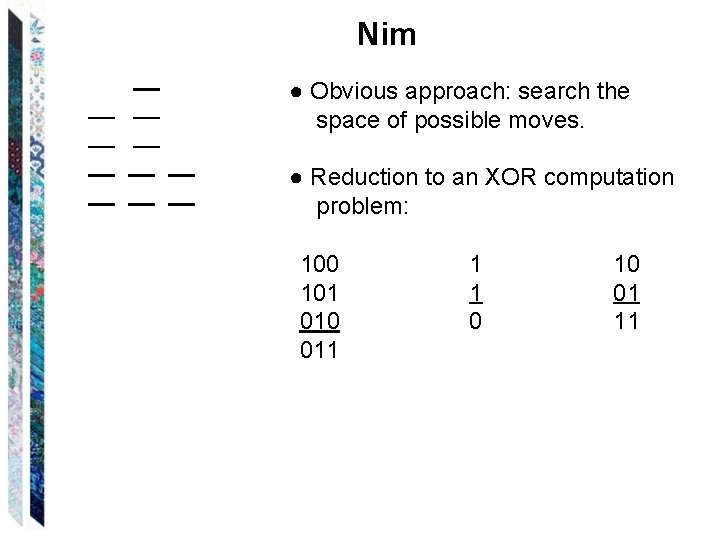
Nim ● Obvious approach: search the space of possible moves. ● Reduction to an XOR computation problem: 100 101 010 011 1 1 0 10 01 11

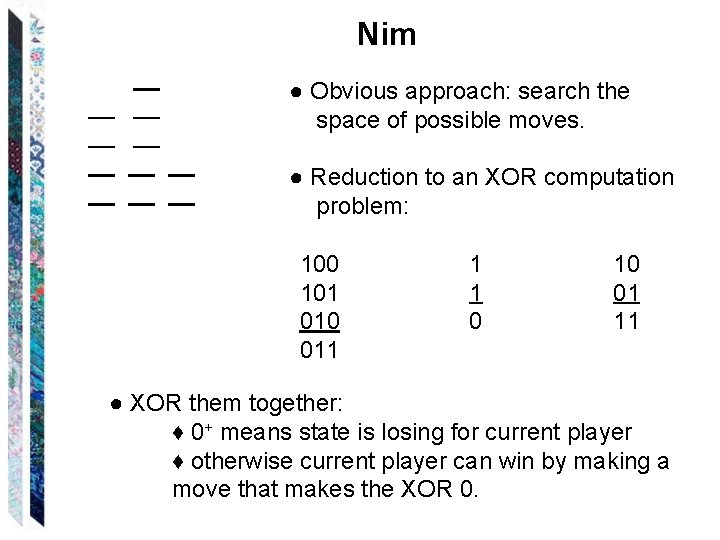
Nim ● Obvious approach: search the space of possible moves. ● Reduction to an XOR computation problem: 100 101 010 011 1 1 0 10 01 11 ● XOR them together: ♦ 0+ means state is losing for current player ♦ otherwise current player can win by making a move that makes the XOR 0.

Correctness Proof of Nim Reduction • If all 0’s, there is no move that preserves all 0’s: • If not all 0’s, there is a move that makes it all 0’s:

Correctness Proof of Nim Reduction • If all 0’s, there is no move that preserves all 0’s: Suppose there were such a move. Then it would change some row n. Since it must subtract at least 1 from the number in row n, it would necessarily change a 1 in some column j to a 0. 11 Since the XOR of that column was 0, it now becomes 1. 01 The only way to return it to 0 would be to alter some other row in column j. But a given move can only alter a single row. So the new XOR will contain at least one 1. 10 00

Correctness Proof of Nim Reduction • If not all 0’s, there is a move that makes it all 0’s: 1. Scan from the left to find the first column, j, that contains a 1 in the XOR row. 2. Choose a row, i, that contains a 1 in column j. Change the 1 to 0. 3. Continue moving from the left. If the XOR row contains a 1 in column j, flip bit (i, j). 101 111 001 011 • At the end, the XOR row is all 0’s because we flipped exactly one bit in every column that had been 1 and no bits in columns that had been 0. • The flipping corresponds to a legal move because it changes only one row and it creates a row that represents a smaller number than the original one.