USING QUANTITATIVE METHODS TO STUDY COMPLEX SYSTEMS David

USING QUANTITATIVE METHODS TO STUDY COMPLEX SYSTEMS David Katerndahl, M. D. , M. A.

Quantitative Approaches To Studying Complex Systems 1. Estimating Complexity 2. Modeling And Simulations 3. Studying Characteristics Of Complex Systems

Quantitative Approaches To Studying Complex Systems Objective 1. 2. 3. To Survey Quantitative Methods Available To Give Examples From Previous Studies To Provide Resources

Studying Characteristics Of Complex Systems 1. Dynamics & Its Components 2. Scale & Emergence 3. Interrelationships & Self-Organization 4. Co-Evolution & Complex Behavior

Dynamics & Its Components Information Gathered l Frequent Changes In State Quantitative Methods Entropy – Nonlinearity l Dynamic Patterns l State Space Girds - Attractors l Cusp Catastrophe Analysis - Bifurcations l

Dynamics & Its Components Time Series Analysis – Requirements Type Of Data = Interval l Number Of Data Points l Traditional 1000 l Time Series Analysis 400 l l l Previous Studies Used 50 -100 Sensible ≥ 50 (Enough To Represent Dynamics) l l Good Measurements 1 -2 Parameters Carefully Collected Approximate Entropy Proven Stable

Dynamics & Its Components Time Series Analysis – Requirements l Data Interval l Shorter – Have More Data Points l l l Longer - Average Out Artificial Dependencies l l Can Produce Artificial Dependencies Spurious Evidence of Nonlinearity Lose Evidence of Nonlinearity Even if Present Based on Logical Interval for Measurement

Dynamics & Its Components Entropy (≥ 0) l Information Kolmogorov (Grassberger) Entropy l Liz-Zempel Entropy l Topological Entropy – Orbital Decomposition l Regularity - Approximate Entropy l Interpretation: High Entropy, High Irregularity l

Dynamics & Its Components Study: Effects Of Medications On Mood Regularity Approximate Entropy Yeragani et al, Bipolar Disorders 2003

Dynamics & Its Components Different Dynamic Patterns In A Single System

Dynamics & Its Components Dynamic Patterns Analysis – STEP 1 l Phase Plot – x(t) vs. x(t-1) Dynamics Periodic Chaotic Random Pattern Loop, Oscillation Other Fills Space

PHASE PLOTS Periodic Random Chaotic P 04 P 03 N 01

Dynamics & Its Components Dynamic Patterns Analysis – STEP 1 l ARIMA Modeling (p, d, q) – Relation To Random Shocks Model Autoregression Integration Moving Average Cause Previous Observation + Random Shock Differencing Current Shock + Portions Of Previous Shocks

Dynamics & Its Components Dynamic Patterns Analysis – STEP 2 l Lyapunov Exponent – Sensitivity To Initial Conditions l Related To Speed Of Divergence l (e. g. 0. 693 = separation doubles each iteration) Dynamics Periodic Chaotic Random Sign + +/-

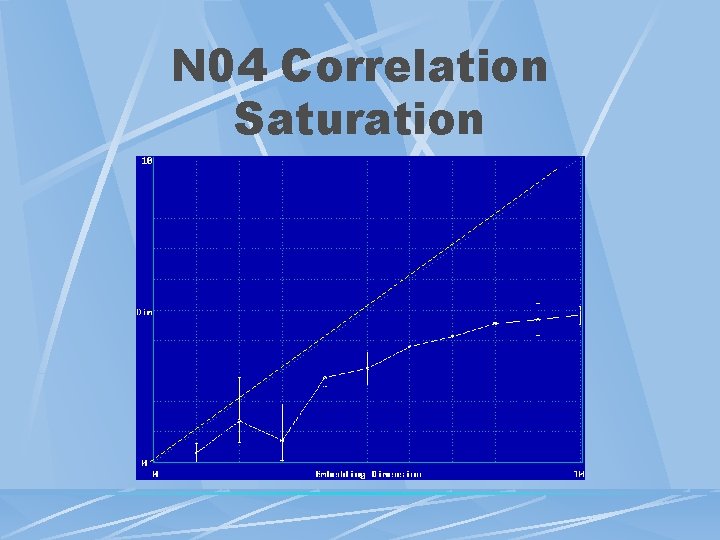
Dynamics & Its Components Dynamic Patterns Analysis – STEP 2 l Correlation Dimension Saturation – Attractor Cd Measures Correlation Of Points – Attractor Dimension l Plot Cd vs Embedding Dimension (Possible Space) l Saturation - Cd Falls Off Diagonal l

N 04 Correlation Saturation

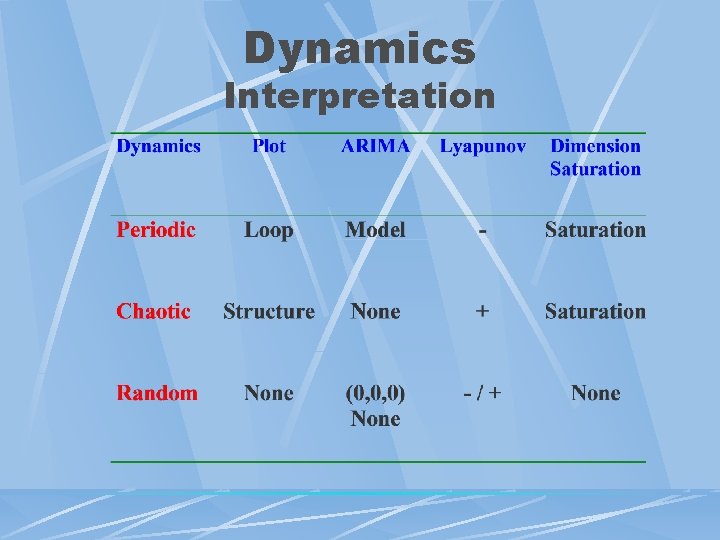
Dynamics Interpretation

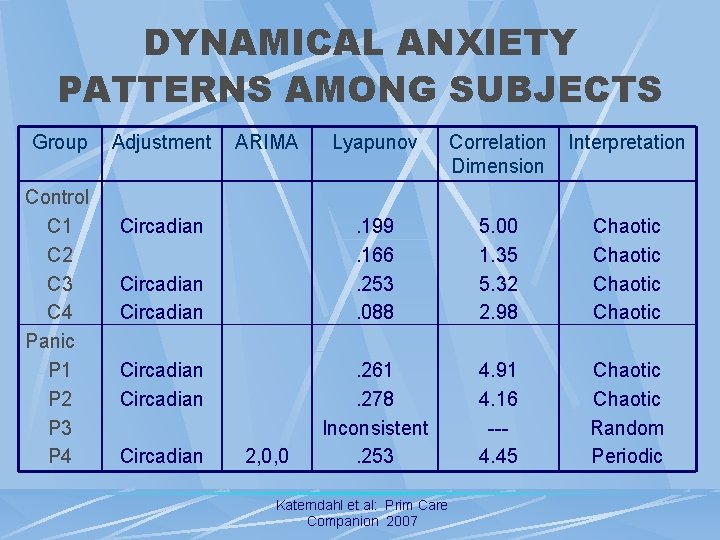
DYNAMICAL ANXIETY PATTERNS AMONG SUBJECTS Group Control C 1 C 2 C 3 C 4 Panic P 1 P 2 P 3 P 4 Adjustment ARIMA Circadian Circadian 2, 0, 0 Lyapunov Correlation Dimension Interpretation . 199. 166. 253. 088 5. 00 1. 35 5. 32 2. 98 Chaotic . 261. 278 Inconsistent. 253 4. 91 4. 16 --4. 45 Chaotic Random Periodic Katerndahl et al: Prim Care Companion 2007

Interpretation Periodic Dynamics l Characteristics Low Dimensional l Few Degrees Of Freedom l Closed System l l Properties Decreased Resources, Increased Constraints l Linkage Between Action And Consequences l

Interpretation Chaotic Dynamics l Characteristics l l Low Dimensional Few Degrees Of Freedom Closed System Properties l l l Feedback Variable In Strength And Direction Delay Between Action And Consequences Sensitive And Resistant Expansion And Contraction Terms Sufficient Resources, Few Constraints

Interpretation Critical Systems l Characteristics Open System l Multiple Factors l Coupled Components l l Properties Differing Component Thresholds/Response l Events Same Regardless Of Consequences l High Dimensional Chaos ≈ Randomness l

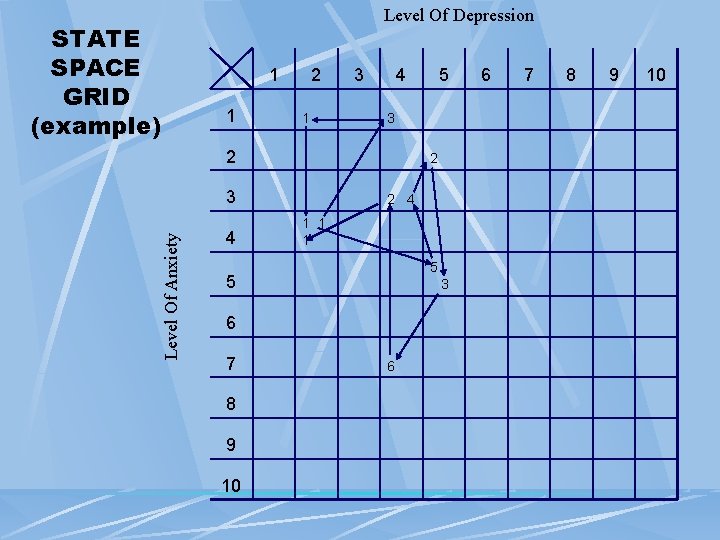
Dynamics & Its Components State Space Grids - 2 -Way Time Series Identification Of Attractors l Evolution Of Attractors l l Requirements Co-Variation Of 2 Variables l Ordinal Categories (5 -10) l Sample Size: Studies ≥ 60 l

STATE SPACE GRID (example) Level Of Depression 1 1 2 1 3 4 3 2 2 Level Of Anxiety 3 4 2 4 1 1 1 5 5 3 6 7 8 9 10 5 6 6 7 8 9 10

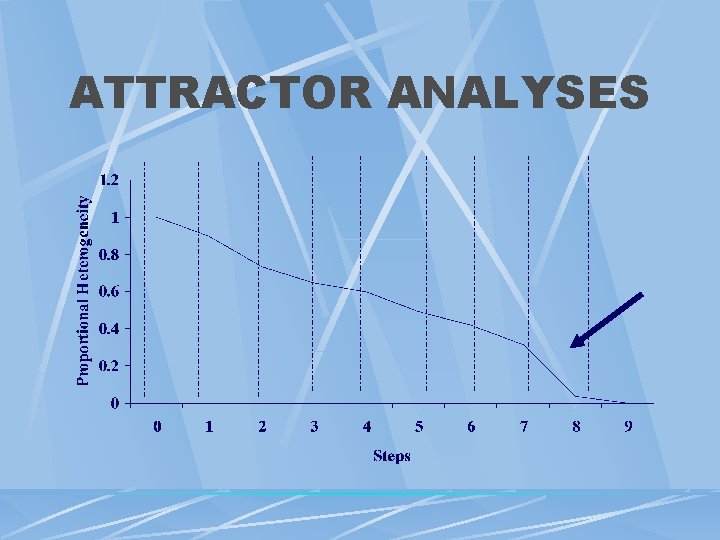
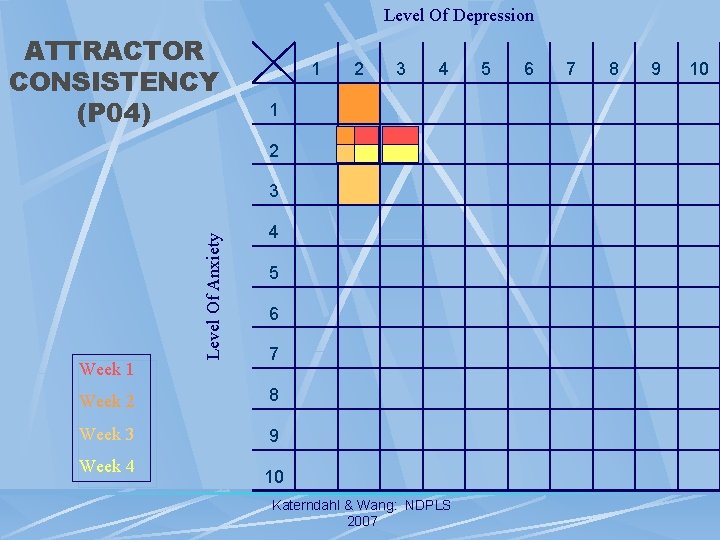
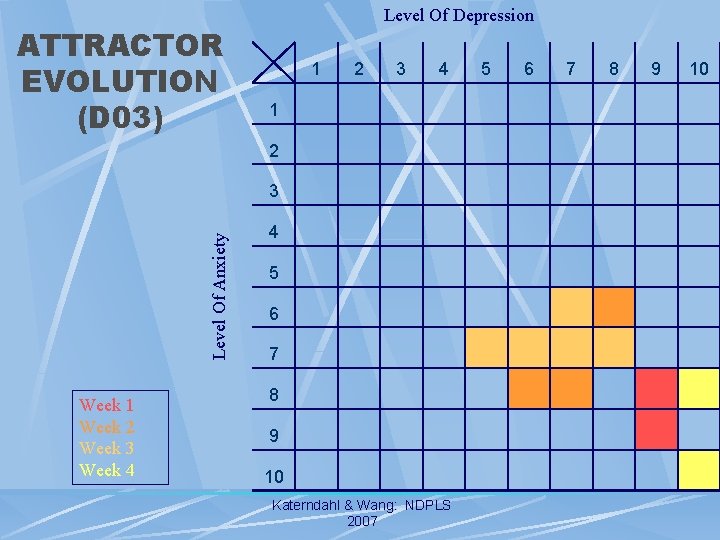
ATTRACTOR ANALYSES State Space Grid l Plot State #1 (1 -10) versus State #2 (1 -10) Identify Attractors l l Compute Heterogeneities (Cell Deviation From Randomness) Winnowing Using Scree Attractiveness l l Influence = Probability Outside Event Moves To Attractor Stability = Once Exited From Attractor, Time Until Returned Consistency = Recurrence Of Attractor Over Time

ATTRACTOR ANALYSES

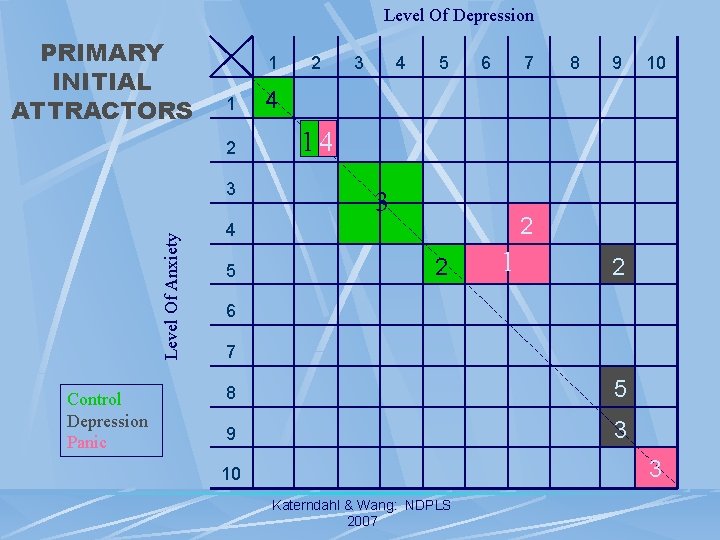
Level Of Depression PRIMARY INITIAL ATTRACTORS 1 1 2 Level Of Anxiety 3 Control Depression Panic 2 3 4 5 6 8 9 10 4 14 3 2 4 5 7 2 1 2 6 7 8 5 9 3 33 10 Katerndahl & Wang: NDPLS 2007

Level Of Depression ATTRACTOR CONSISTENCY (P 04) 1 2 3 4 1 2 Week 1 Level Of Anxiety 3 4 5 6 7 Week 2 8 Week 3 9 Week 4 10 Katerndahl & Wang: NDPLS 2007 5 6 7 8 9 10

ATTRACTOR EVOLUTION (D 03) Level Of Depression 1 2 3 4 1 2 Level Of Anxiety 3 Week 1 Week 2 Week 3 Week 4 4 5 6 7 8 9 10 Katerndahl & Wang: NDPLS 2007 5 6 7 8 9 10

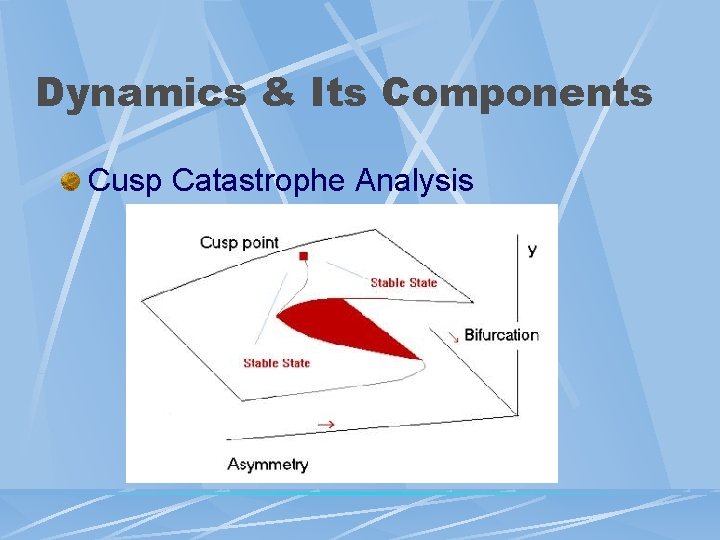
Dynamics & Its Components Cusp Catastrophe Analysis

Dynamics & Its Components Cusp Catastrophe Analysis - Bifurcation 1. Requirements 1. 2. Interval Data Sample Size 1. 2. 3 Variables (Z-transformed) 1. 2. 3. 2. l Predisposition (Asymmetry) Stressor (Bifurcation) Outcome - 2 Time Points Identification Of Bimodality 1. 3. Smaller Number Covering Full Range Better (≥ 50) Prior Studies = 22 -576 Plot Increasing Mean And Standard Deviation Comparison With Linear Models Applications – Health Behaviors l l l Adolescent Smoking & Drinking Eating Behavior Drinking & Driving Speed Decision-Making Attitudinal Change

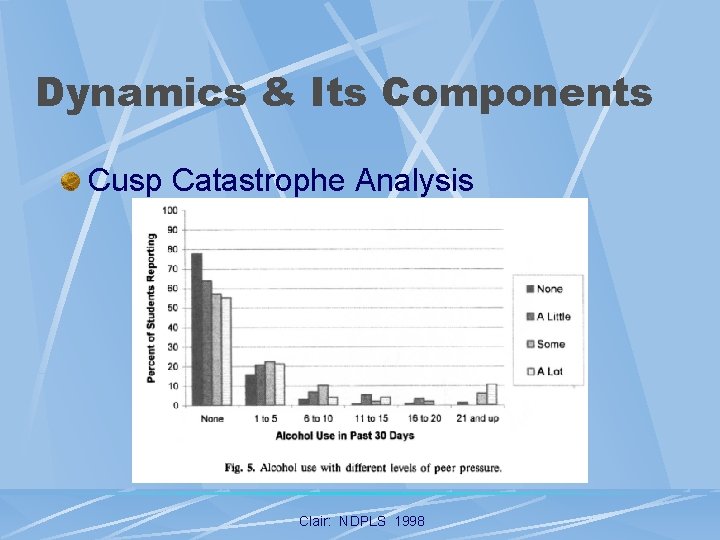
Dynamics & Its Components Cusp Catastrophe Analysis Clair: NDPLS 1998

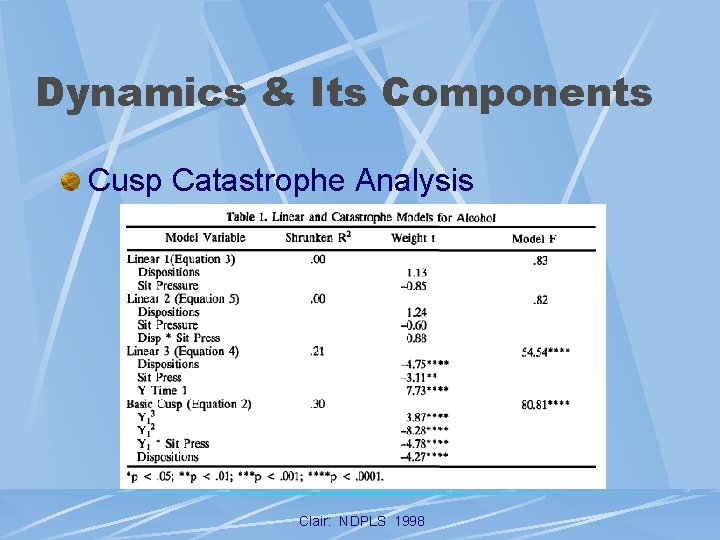
Dynamics & Its Components Cusp Catastrophe Analysis l Models Tested l Linear l Cusp Catastrophe Clair: NDPLS 1998

Dynamics & Its Components Cusp Catastrophe Analysis Clair: NDPLS 1998

Dynamics & Its Components Cusp Catastrophe Analysis l Implications Bimodal Distribution Based On Stressor l Sudden Changes In Behavior l Jumps In Behavior At Different Levels Of Predisposition l At High levels Of Stressor, Certain Values Of Outcome Not Observed l Clair: NDPLS 1998

Scale & Emergence Information Gathered l Changes With Scale Quantitative Methods Hierarchical Modeling l Power Law Distribution l Multiscale Representations l

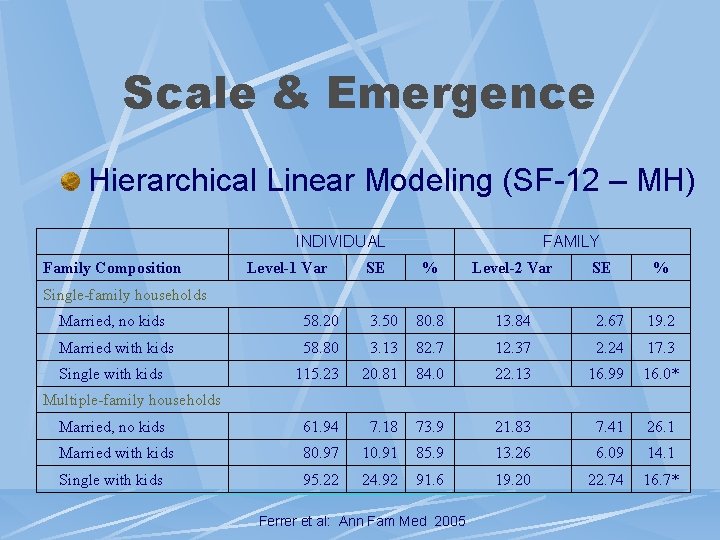
Scale & Emergence Hierarchical Linear Modeling Amount Of Variance With Scale Change l Limitation: Uses Proscribed Groups l Ideal: Diversity Or Variability Of Outcome Variable l l Requirements Interval Outcome l Sample Size: 10/30 l Implication – Multilevel Effects l Application – Practice, Family, Community Effects l

Scale & Emergence Hierarchical Linear Modeling (SF-12 – MH) INDIVIDUAL Family Composition Level-1 Var SE FAMILY % Level-2 Var SE % Single-family households Married, no kids 58. 20 3. 50 80. 8 13. 84 2. 67 19. 2 Married with kids 58. 80 3. 13 82. 7 12. 37 2. 24 17. 3 115. 23 20. 81 84. 0 22. 13 16. 99 16. 0* Married, no kids 61. 94 7. 18 73. 9 21. 83 7. 41 26. 1 Married with kids 80. 97 10. 91 85. 9 13. 26 6. 09 14. 1 Single with kids 95. 22 24. 92 91. 6 19. 20 22. 74 16. 7* Single with kids Multiple-family households Ferrer et al: Ann Fam Med 2005

Scale & Emergence Power Law Distribution l Complex Systems Demonstrate Power Law Dynamics y = β (x)α log y = log β + α log x

Scale & Emergence Power Law Distribution l l l Characteristic Of Complex Systems Sample Size: Typically 700 – 1, 000 s Indicates: l l Single Interconnected System Critical Dynamics l l l Transitional Between Periodic & Chaotic Complex Systems Tuned To Criticality 80/20 Rule Scale Invariance Long Term Memory Involved 2 Homeostatic Systems Interacting

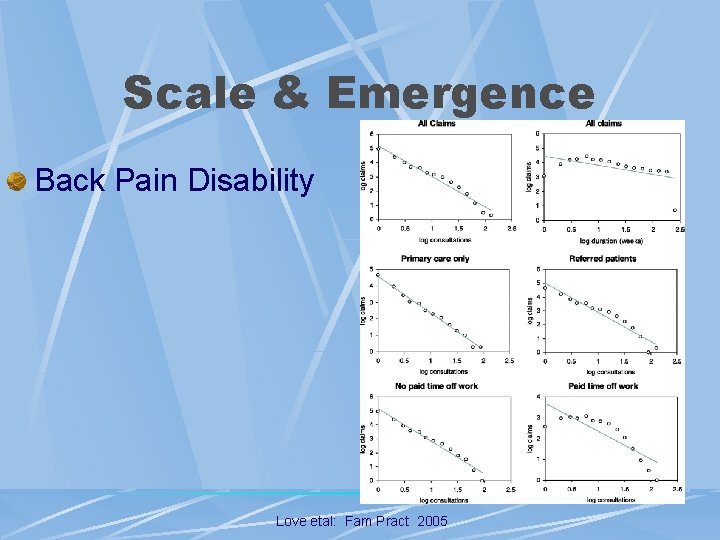
Scale & Emergence Power Law Distribution l Log-Log Plotting Of Frequency versus Severity l l Preferable: ≥ 3 -Fold Exponent Range Previous Applications - Ubiquitous l Alcoholism l l Number Of Alcoholics versus Number Of Inpatient Detoxifications Low Back Pain l Number Of LBP Sufferers versus Time Of Work

Scale & Emergence Back Pain Disability Love etal: Fam Pract 2005

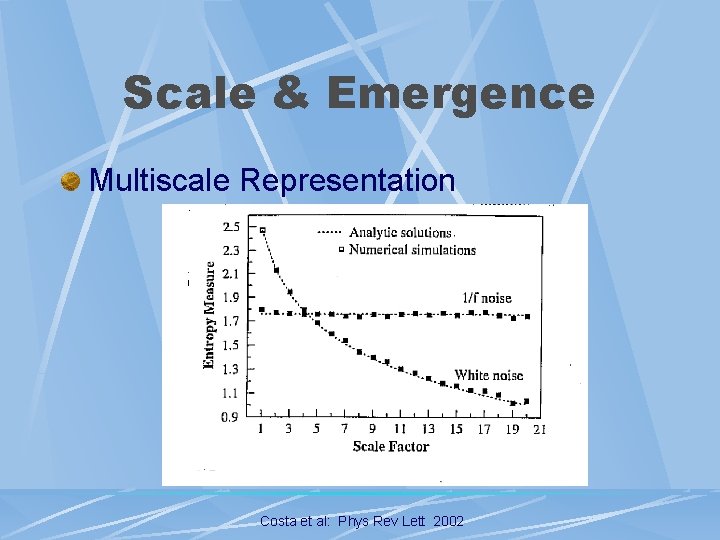
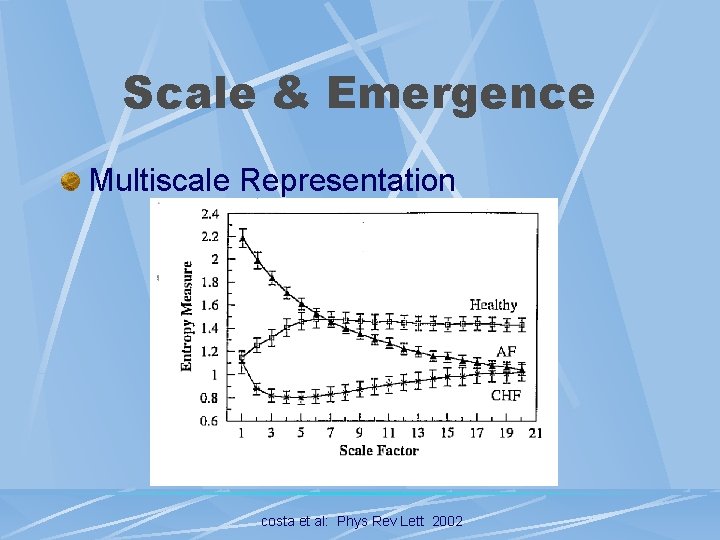
Scale & Emergence Multiscale Representation l Changes Versus Scale Number Of Datapoints l Time l l Variables Scale: Ordinal l Outcome: Interval l

Scale & Emergence Multiscale Representation Costa et al: Phys Rev Lett 2002

Scale & Emergence Multiscale Representation costa et al: Phys Rev Lett 2002

Interrelationships & Self-Organization Information Gathered l l l Interactions Connectedness Clustering Quantitative Methods l l Social Network Analysis Power Law Distribution Vector Autoregression Neural Networks

Interrelationships & Self-Organization Social Network Analysis l l Assesses Interconnectedness Of Group Of Agents Measurements Of Relationship l l Sample Size: n ≤ 130 -150 For Interviews/Surveys Considerations l l l Directed Versus Undirected Binary, Ordinal, Interval Boundary Effects Of Missing Data Outcomes l Network l l l Average Connectedness Centrality & Distance Between Agents Degree Of Constraint Clustering Agents l l Centrality Betweenness

Interrelationships & Self-Organization Social Network Analysis (Practice) Scott et al: Ann Fam Med

Interrelationships & Self-Organization Social Network Analysis Density – Connectedness l Clustering – In Groups l Indegree - Consult Particular l Outdegree - Consult Others l Scott et al: Ann Fam Med, 2005

Interrelationships & Self-Organization Power Law Distribution l Relationship Between 2 Variables State Space Grid Of Co-Variability l Log-Log Plot l l l Quantity Per Cell (Maximum-To-Minimum) Rank Order Slope Is Unique To Sample Previous Application l Daily Inpatient Levels Of Agitation versus Social Interaction

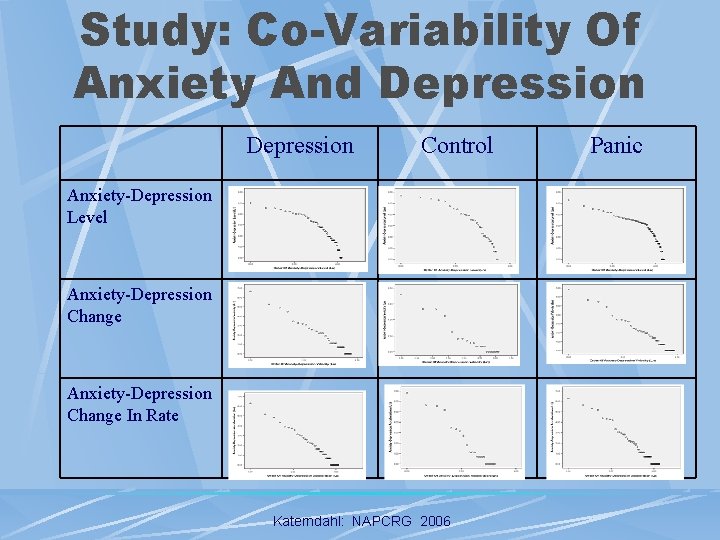
Study: Co-Variability Of Anxiety And Depression State Space Grid (Anxiety versus Depression) l l Levels Of Anxiety And Depression Changes In Anxiety And Depression Change In Rate Of Change Of Anxiety And Depression Level of Anxiety Level of Depression l 1 2 3 4 5 6 7 8 9 10 1 0 0 0 0 2 0 1 4 0 0 0 0 3 0 0 1 3 2 2 0 0 4 7 0 0 2 0 0 0 5 1 2 7 2 5 7 26 1 16 4 6 1 5 5 17 59 44 37 49 26 9 7 0 5 2 4 16 38 52 55 28 10 8 0 7 6 11 13 26 81 70 29 12 9 4 11 6 7 13 22 16 93 91 53 10 4 0 2 5 5 27 16 55 68 153 Katerndahl: NAPCRG 2006

Study: Co-Variability Of Anxiety And Depression Control Anxiety-Depression Level Anxiety-Depression Change In Rate Katerndahl: NAPCRG 2006 Panic

Study: Co-Variability Of Anxiety And Depression B R 2 Control B R 2 Panic B R 2 Anxiety-Depression Level -1. 36 . 830 -1. 73 . 850 -1. 21 . 752 Anxiety-Depression Change -1. 81 . 986 -2. 49 . 939 -1. 89 . 986 Anxiety-Depression Change In Rate -1. 68 . 981 -2. 48 . 956 -1. 75 . 979 Katerndahl: NAPCRG 2006

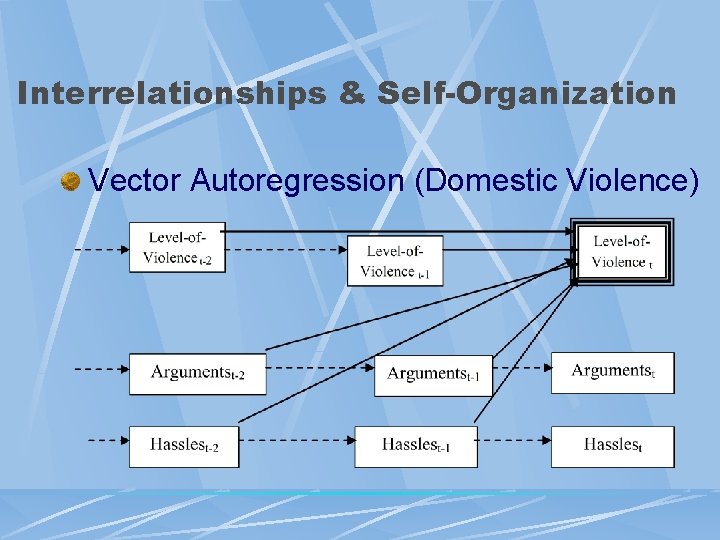
Interrelationships & Self-Organization Vector Autoregression Use Multiple Time Series l Multiple Linear Lagged Relationships l Evolution & Interdependencies l Data – Interval l Sample Size: Critical Values For As Few As 25 -50 Datapoints l

Interrelationships & Self-Organization Vector Autoregression (Domestic Violence)

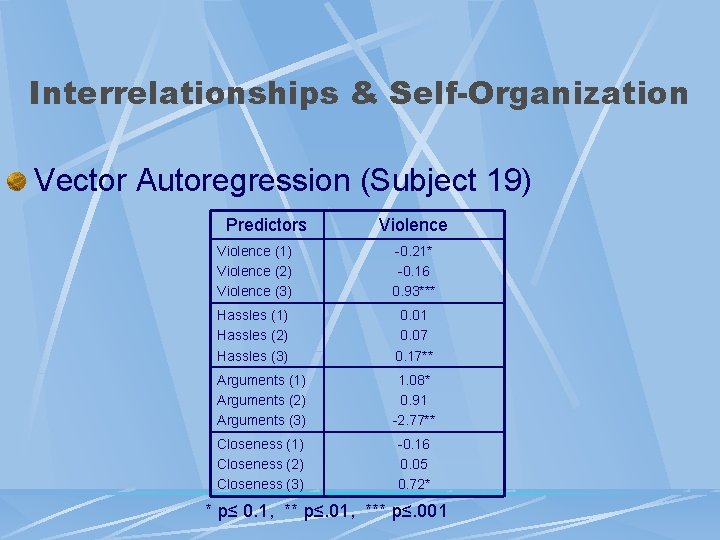
Interrelationships & Self-Organization Vector Autoregression (Subject 19) Predictors Violence (1) Violence (2) Violence (3) -0. 21* -0. 16 0. 93*** Hassles (1) Hassles (2) Hassles (3) 0. 01 0. 07 0. 17** Arguments (1) Arguments (2) Arguments (3) 1. 08* 0. 91 -2. 77** Closeness (1) Closeness (2) Closeness (3) -0. 16 0. 05 0. 72* * p≤ 0. 1, ** p≤. 01, *** p≤. 001

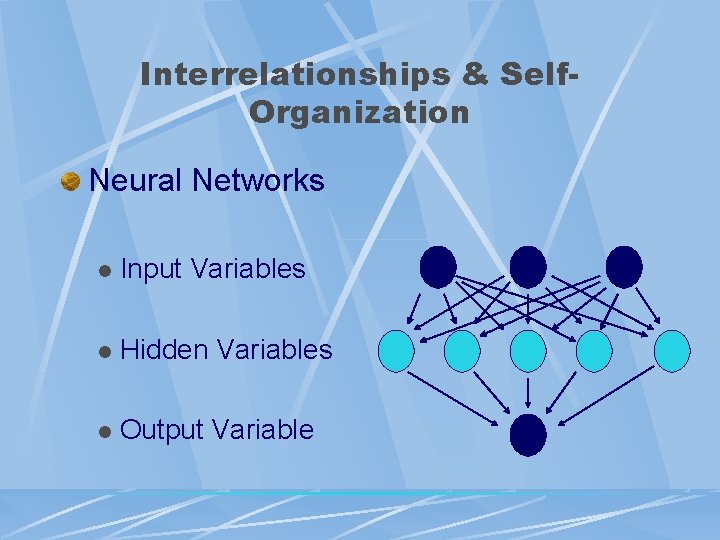
Interrelationships & Self-Organization Neural Networks Nonlinear Interrelationships l Goal: Predict Outcome From Inputs l Re-runs Analysis, Adjusting Weights Each Time l Preferred: Learning Set & Test (Validation) Set l Sample Size: ≥ 200 For Each Set l

Interrelationships & Self. Organization Neural Networks l Input Variables l Hidden Variables l Output Variable

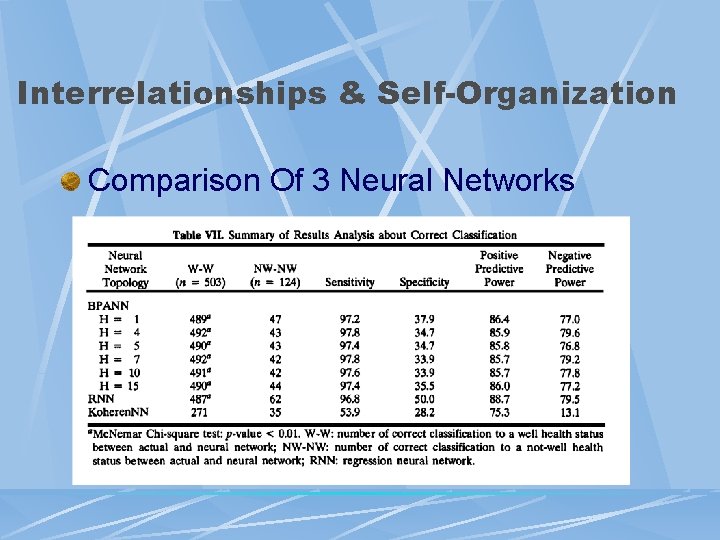
Interrelationships & Self-Organization Comparison Of 3 Neural Networks

Co-Evolution & Complex Behavior Information Gathered l l Changes In State Of 2 Variables Time Series Data Quantitative l l Phase Plane Plot Cross-Approximate Entropy Differential Structural Equation Modeling Vector Autoregression

Co-Evolution & Complex Behavior Phase Plane Plot Differences Between 2 Variables l Visual Analysis Of Co-Variation l Relative Frequencies Of Quadrants Visited l

Complex System Behavior Phase Plane Plot ΔX ΔY

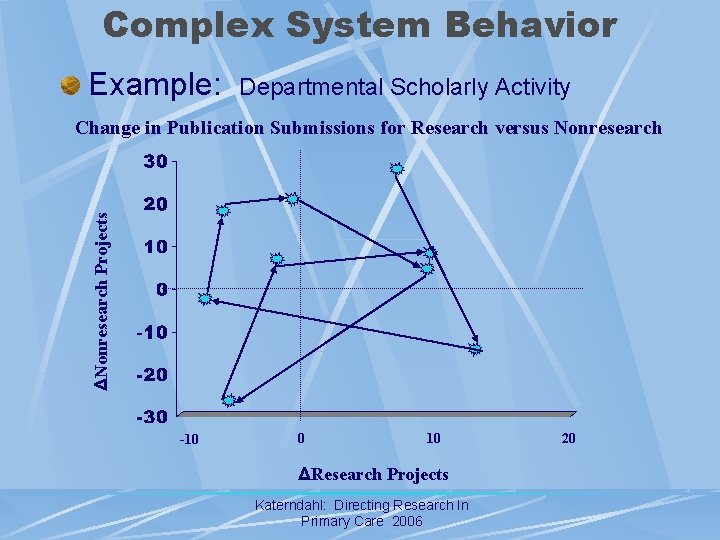
Complex System Behavior Example: Departmental Scholarly Activity ΔNonresearch Projects Change in Publication Submissions for Research versus Nonresearch -10 0 10 ΔResearch Projects Katerndahl: Directing Research In Primary Care 2006 20

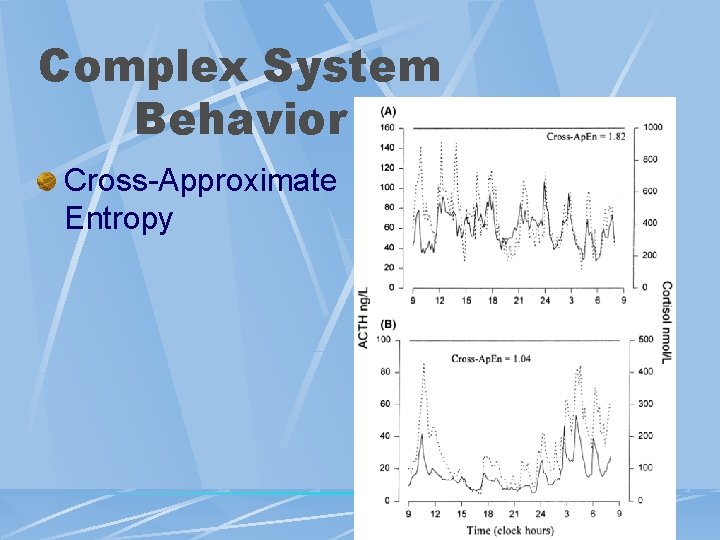
Complex System Behavior Cross-Approximate Entropy Measures Asynchrony Between 2 Time Series l Sample Aize: Used 144 -168 l Higher Value, More Synchronous l

Complex System Behavior Cross-Approximate Entropy

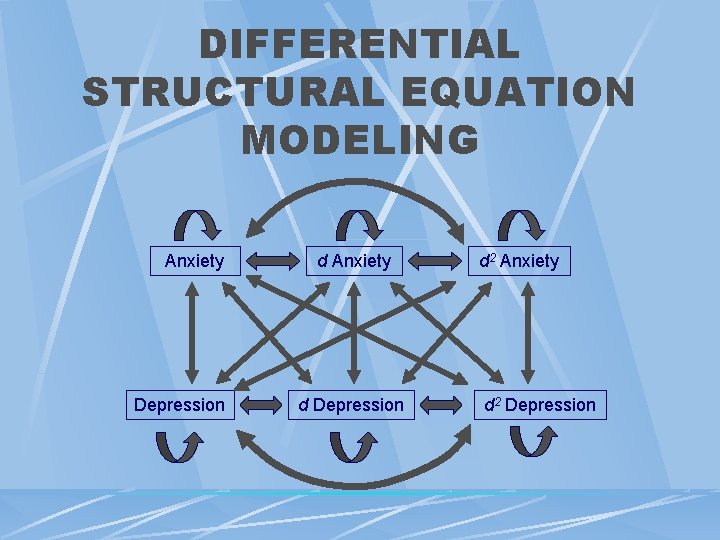
Differential Structural Equation Modeling (DSEM) Extension Of SEM Sample Size: Originally 165 Models Derivatives Of Scores l l Velocity = Difference Between Adjacent Scores Acceleration = Difference Between Adjacent Velocities Reflects Forces l l Equilibrium (Linearity? ) – Inverse Acceleration And Score Friction – Inverse Acceleration And Velocity Study Correlation Between Multiple Dynamic Systems

DIFFERENTIAL STRUCTURAL EQUATION MODELING Anxiety Depression d Anxiety d Depression d 2 Anxiety d 2 Depression

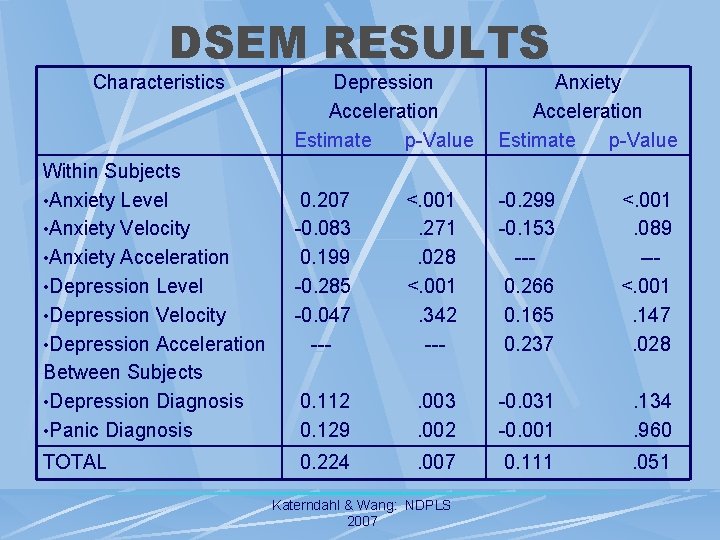
DSEM RESULTS Characteristics Within Subjects • Anxiety Level • Anxiety Velocity • Anxiety Acceleration • Depression Level • Depression Velocity • Depression Acceleration Between Subjects • Depression Diagnosis • Panic Diagnosis TOTAL Depression Acceleration Estimate p-Value Anxiety Acceleration Estimate p-Value 0. 207 -0. 083 0. 199 -0. 285 -0. 047 --- <. 001. 271. 028 <. 001. 342 --- -0. 299 -0. 153 --0. 266 0. 165 0. 237 <. 001. 089 --<. 001. 147. 028 0. 112 0. 129 . 003. 002 -0. 031 -0. 001 . 134. 960 0. 224 . 007 0. 111 . 051 Katerndahl & Wang: NDPLS 2007

Co-Evolution & Complex Behavior Vector Autoregression Use Multiple Time Series l Multiple Linear Lagged Relationships l Focus On Multiple Outcomes l

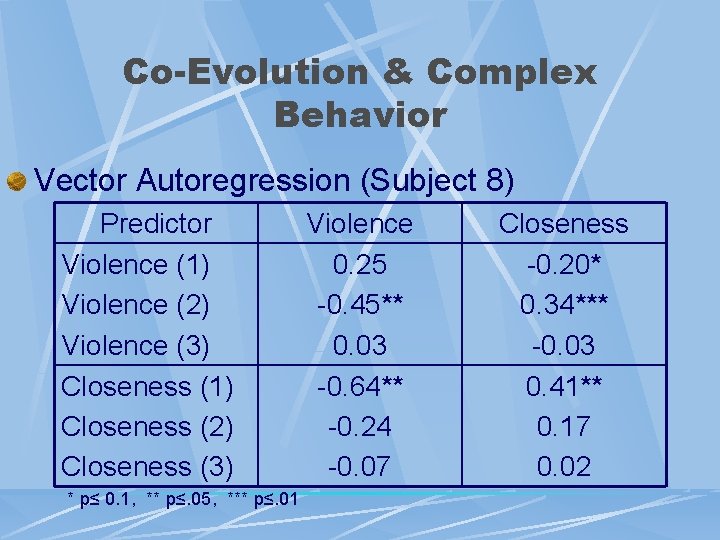
Co-Evolution & Complex Behavior Vector Autoregression (Subject 8) Predictor Violence (1) Violence (2) Violence (3) Closeness (1) Closeness (2) Closeness (3) * p≤ 0. 1, ** p≤. 05, *** p≤. 01 Violence 0. 25 -0. 45** 0. 03 -0. 64** -0. 24 -0. 07 Closeness -0. 20* 0. 34*** -0. 03 0. 41** 0. 17 0. 02

SUMMARY Variety Of Methods Available 1. 2. 3. 4. Dynamics & Its Components Scale & Emergence Interrelationships & Self-Organization Co-Evolution & Complex Behavior Primary Care Applications l l Few Studies Performed Limitations To Methods Resources Limited

The End