Using Pythagoras Theorem L O Use Pythagoras Theorem

Using Pythagoras’ Theorem L. O. Use Pythagoras Theorem to find missing sides on a triangle Level 7 Solve real-life problems using Pythagoras Theorem Level 8 We are learning this because… 3000 years ago the Egyptians used Pythagoras Theorem to build o the Great Pyramids using knotted rope to make a 90 angle using a 3, 4, 5 triangle. Today builders using pieces of woodowith length 3 ft, 4 ft, 5 ft to the same thing to get a perfect 90 right angle

Pythagoras’ Theorem I was born at Samos, in Greece, and lived from 580 to 500 B. C. I was a Mathematician who became famous for discovering something unique about right – angled triangles. Now you are going to try to find out what I discovered!!

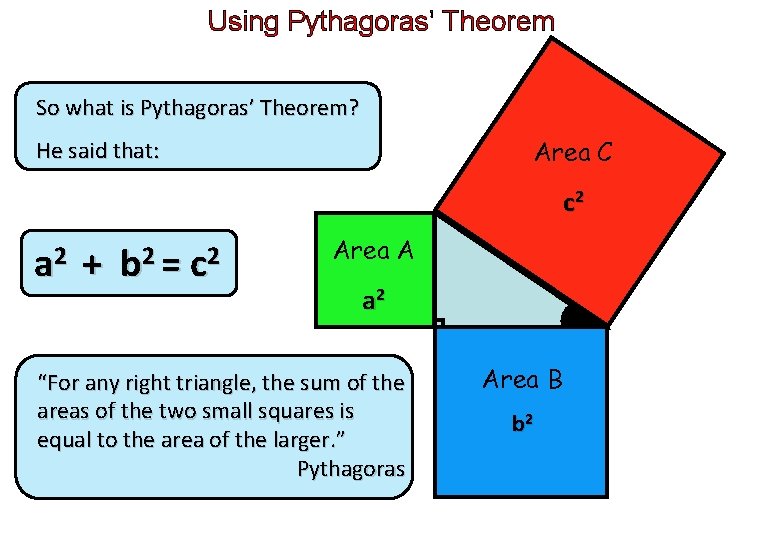
Using Pythagoras’ Theorem So what is Pythagoras’ Theorem? Area C He said that: c 2 a 2 + b 2 = c 2 c Area A a 2 “For any right triangle, the sum of the areas of the two small squares is equal to the area of the larger. ” Pythagoras a b Area B b 2

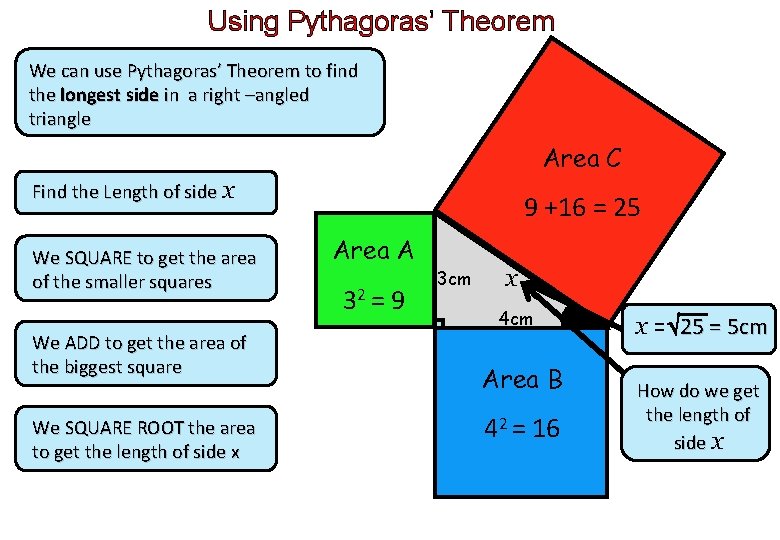
Using Pythagoras’ Theorem We can use Pythagoras’ Theorem to find the longest side in a right –angled triangle Area C Find the Length of side x We SQUARE to get the area of the smaller squares We ADD to get the area of the biggest square We SQUARE ROOT the area to get the length of side x 9 +16 = 25 Area A 32 = 9 3 cm x 4 cm Area B 42 = 16 x = 25 = 5 cm How do we get the length of side x

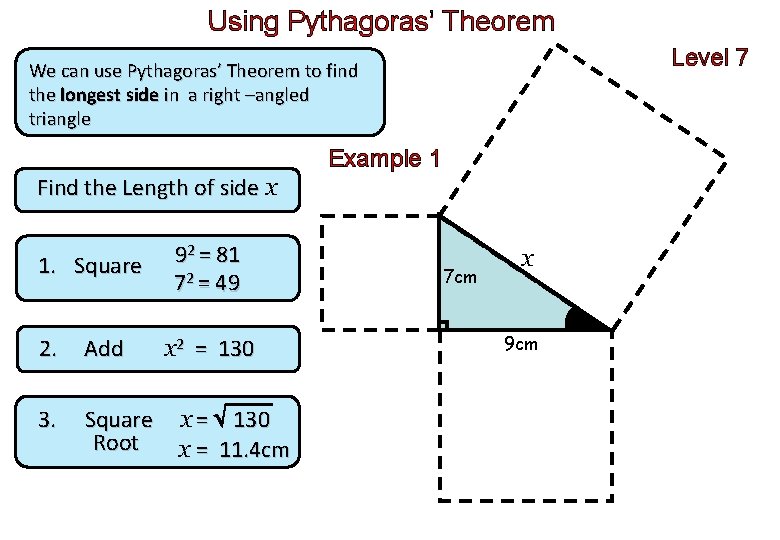
Using Pythagoras’ Theorem Level 7 We can use Pythagoras’ Theorem to find the longest side in a right –angled triangle Example 1 Find the Length of side x 1. Square 2. Add 3. Square Root 92 = 81 72 = 49 x 2 = 130 x = 11. 4 cm 7 cm x 9 cm

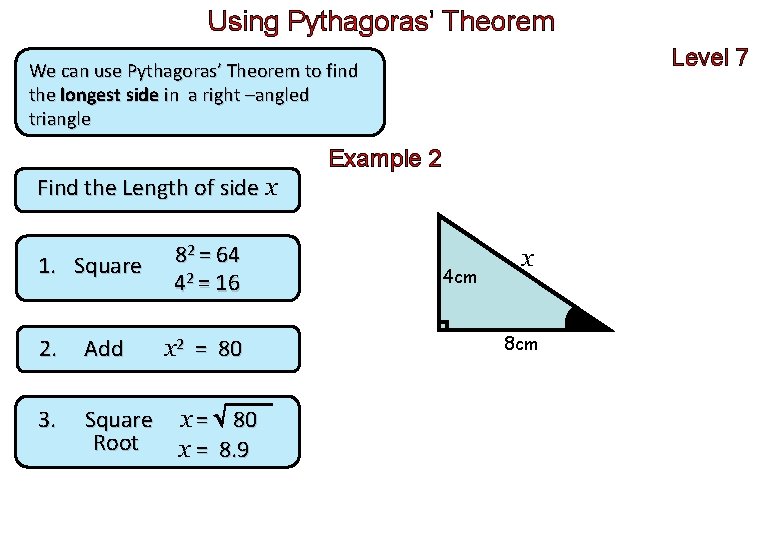
Using Pythagoras’ Theorem Level 7 We can use Pythagoras’ Theorem to find the longest side in a right –angled triangle Example 2 Find the Length of side x 1. Square 2. Add 3. Square Root 82 = 64 42 = 16 x 2 = 80 x = 8. 9 4 cm x 8 cm

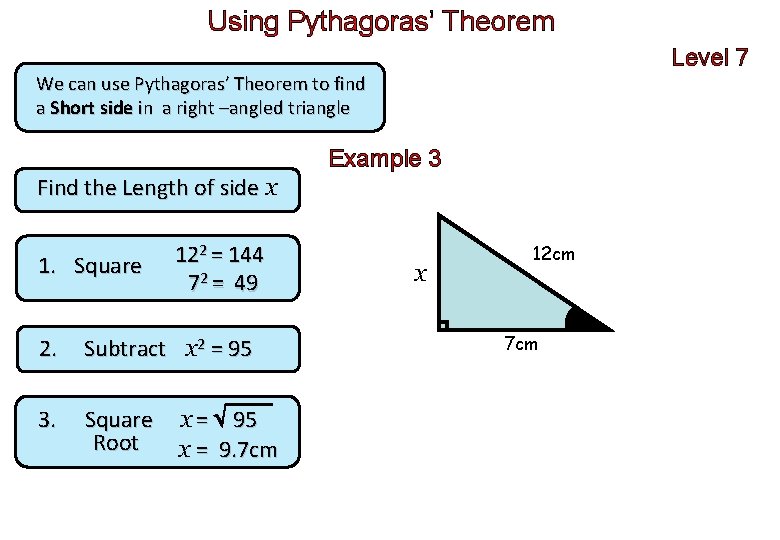
Using Pythagoras’ Theorem Level 7 We can use Pythagoras’ Theorem to find a Short side in a right –angled triangle Example 3 Find the Length of side x 1. Square 122 = 144 72 = 49 2. Subtract x 2 = 95 3. Square Root x = 95 x = 9. 7 cm x 12 cm 7 cm

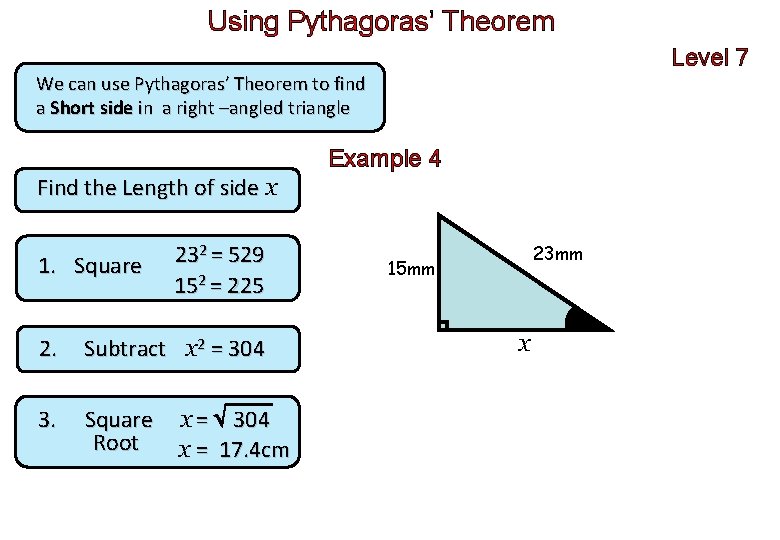
Using Pythagoras’ Theorem Level 7 We can use Pythagoras’ Theorem to find a Short side in a right –angled triangle Example 4 Find the Length of side x 1. Square 232 = 529 152 = 225 2. Subtract x 2 = 304 3. Square Root x = 304 x = 17. 4 cm 23 mm 15 mm x

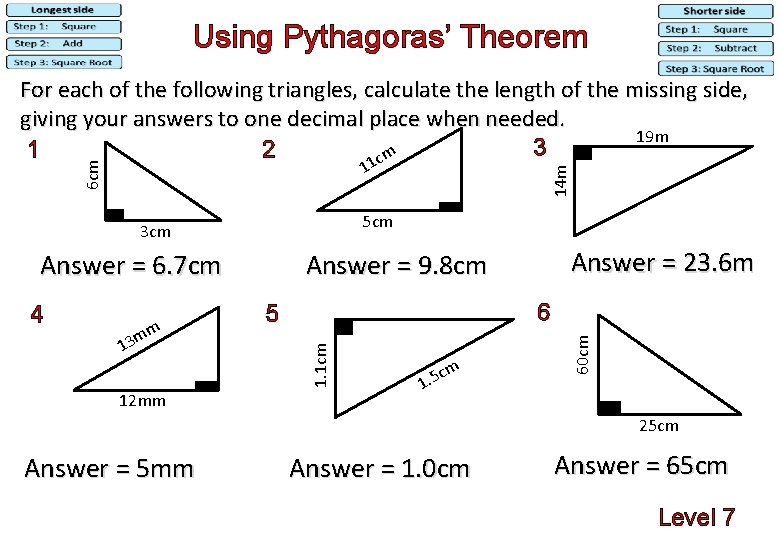
Using Pythagoras’ Theorem For each of the following triangles, calculate the length of the missing side, giving your answers to one decimal place when needed. 19 m 3 2 1 cm 5 cm 3 cm 12 mm c 1. 5 m 60 cm 13 6 5 1. 1 cm mm Answer = 23. 6 m Answer = 9. 8 cm Answer = 6. 7 cm 4 14 m 6 cm 11 25 cm Answer = 5 mm Answer = 1. 0 cm Answer = 65 cm Level 7

Using Pythagoras’ Theorem 7 Calculate the length of the diagonal of this square. 6 cm 8 If a right angle has short lengths 14 cm and 8 cm, what is the length of the longest side. Answer = 16. 1 cm Answer = 8. 5 cm 9 Calculate the height of this isosceles triangle. 10 12 cm Answer = 11. 3 cm 12 cm 8 cm Calculate the base of this isosceles triangle. Answer = 12 cm 10 cm 8 cm

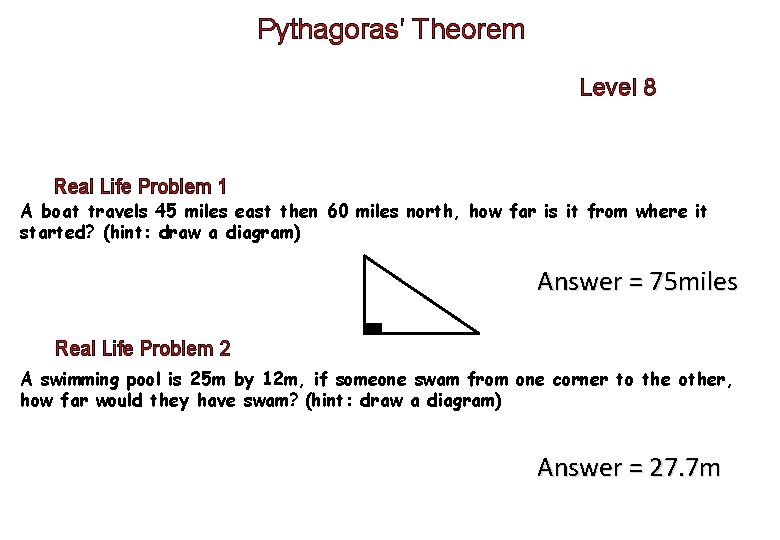
Pythagoras’ Theorem Level 8 Real Life Problem 1 A boat travels 45 miles east then 60 miles north, how far is it from where it started? (hint: draw a diagram) Answer = 75 miles Real Life Problem 2 A swimming pool is 25 m by 12 m, if someone swam from one corner to the other, how far would they have swam? (hint: draw a diagram) Answer = 27. 7 m

Pythagoras’ Theorem Real Life Problem 3 Level 8 A ladder which is 4 m long leans against a wall, the bottom of the ladder is 1. 5 m from the bottom of the wall, how high up the wall does the ladder go? (hint: draw a diagram) Answer = 3. 7 m Real Life Problem 4 A rope of length 10 m is stretched from the top of a pole 3 m high until it reaches the ground. How far is the end of the rope to the base of the pole. (hint: draw a diagram) Answer = 9. 5 m