Using Pulsations to Test Stellar Evolution Models Joyce

Using Pulsations to Test Stellar Evolution Models Joyce A. Guzik Thermonuclear Applications Group, X-2 Los Alamos National Laboratory April 15, 2002 12/23/2021 1

Outline ®Pulsating star locations on the HR Diagram ®Pulsation modes and driving – Period-mean density relation – nonradial oscillations, p-modes and g-modes – kappa/gamma effect driving ®Solar oscillations (helioseismology) ® Attempts at asteroseismology (example: delta Scuti star FG Vir) 12/23/2021 2

From Christensen. Dalsgaard 2000 12/23/2021 3

Period-Mean Density Relation = dynamical frequency ~ 1 / free fall time over the distance of a stellar radius ~ fundamental model frequency For homologous stars (same density stratification), oscillation frequencies scale approximately as sqrt(mean density) 12/23/2021 4

Solutions of stellar pulsation equations (1) ®Assume spherical symmetry, linear perturbations, sinusoidal time dependence – Allow both radial and horizontal motions ®Solve coupled equations of continuity, Poisson, and energy – sometimes make adiabatic approx. and Cowling approx. (neglect gravitational potential perturbations) to simplify solutions ®Solutions exist for discrete values of frequency (eigenvalues of equations) See, e. g. , Cox 1974; Hansen and Kawaler 1986; Christensen-Dalsgaard and Dziembowski 2000 12/23/2021 5

Solutions of stellar pulsation equations (2) Pressure perturbation, e. g. , can be written in form with separated variables in spherical coordinates as: From equation of motion, solution for displacement vector has the form: 12/23/2021 6

Solutions of stellar pulsation equations (3) and are radial and horizontal displacements, and are functions of Lamb Frequency Brunt-Vaisala or buoyancy frequency These two frequencies determine the propagation regions for pressure (acoustic) and gravity waves within a star 12/23/2021 7

From J. P. Cox 1974 12/23/2021 8

p-and g-mode propagation regions for ZAMS solar model from Hansen and Kawaler 1994 12/23/2021 9

Spherical Harmonics 12/23/2021 From Toomre 1984 10

Solar radial eigenfuction amplitudes From Toomre 1984 12/23/2021 11

Pulsation driving by kappa/gamma effect (1) ® Radial and nonradial oscillations of most types of variable stars are driven by the kappa/gamma (kappa as in opacity, gamma as in adiabatic indices) effect, due to the effects of ionization of H, He, C, O, or Fe in stellar envelopes. – H, He ionizes ~10, 000 K – He+ ionizes ~50, 000 K – k-enhancement due to Fe ionization ~ 200, 000 K See, e. g. , Bohm-Vitense 1992; Hansen and Kawaler 1986; Mihalas and Binney 1981 12/23/2021 12

Pulsation driving by kappa/gamma effect (2) Linearizing the diffusion equation, and assuming a power-law opacity: For a non-ionizing region, G 3 = 5/3, s~3. 5, n~1, and When region is compressed and heated, more radiation leaks out. For an ionization region, G 3 --> 1, s < 0, and (for +C) Less radiation leaks out when a region is compressed and heated, and radiation is dammed up. 12/23/2021 13

Kappa Effect Driving Stellar Interior k H, He He+ Fe Stellar Surface * T, r Layer compressed T, k Radiation blocked, pressure increases 12/23/2021 Layer expands T, k Radiation escapes, pressure decreases 14

Pulsation driving by kappa/gamma effect (3) ®Particular oscillation modes can be stable or unstable depending on whether: – region of star contributing significantly to mechanical response is in a driving region – driving in one region is not overcome by radiative damping in another region (integrated work/zone) ®The kappa/gamma effect is weakened or disabled if convection can instead transport enough of the luminosity in the ionization region. (Mechanisms such as “convective driving” and “convective blocking” have also been proposed to explain pulsations of white dwarf and g Dor stars) 12/23/2021 15

Example Work plot for g Doradus model g-mode Guzik et al. Ap. JL 542, L 57 (2000) 12/23/2021 16

Helioseismology ® Solar Oscillations Discovered in 1960 (Leighton, Noyes & Simon) ® Explained as global resonant acoustic modes of the Sun in 1970 (Ulrich, Leibacher, & Stein) ® Extensive application to test physics of solar models and derive internal structure of Sun in 1980 s (helioseismology) ® Attempt to apply technique to other stars in 1990 s (asteroseismology) 12/23/2021 17

Doppler velocity observations of solar disk From Toomre 1984 12/23/2021 18

From Toomre 1984 12/23/2021 19

From Christensen. Dalsgaard 2000 12/23/2021 20

12/23/2021 21

Sound speed differences between model and seismic results using LLNL OPAL and LANL LEDCOP opacities Neuforge-Verheecke et al. , Ap. J 561, 450 (2001) 12/23/2021 22

From Christensen-Dalsgaard et al. 1991 12/23/2021 23

Solar Interior Rotation as inferred from inversions at 0°, 30° and 60° latitude From Chaplin et al. 1999 12/23/2021 24

What did we learn from helioseismology? ® Convection zone helium abundance – 0. 248 ± 0. 001 (e. g. Basu 1998) ® Radius of convection zone base – 0. 7135 ± 0. 0005 R (e. g. Basu 1998) ® Sound speed versus depth – Agrees with modern standard models to within 1 % (e. g. Basu et al. 1998) ® Evidence for diffusive settling of about 10% of initial helium from convection zone during Sun’s lifetime ® Rotation profile versus latitude and depth (e. g. Chaplin et al. 1999) 12/23/2021 25

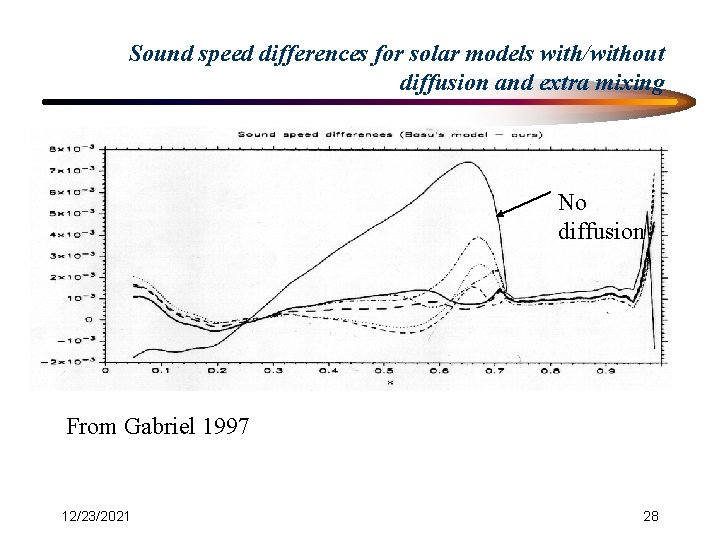
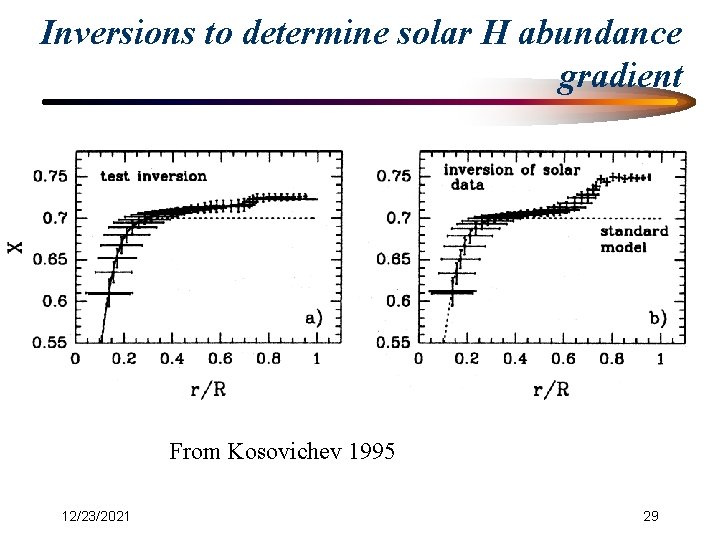
Evidence for Diffusive Helium Settling ® Diffusion calculations predict that about 10% of Helium by mass should settle out of solar convection zone during the Sun’s lifetime ® Observational Evidence: – Convection zone He abundance (Y) determined from signature of He ionization = 0. 248 ± 0. 001 (Basu, 1997), whereas initial Y needed to calibrate solar model to present solar luminosity is 0. 274. – Much improved agreement between calculated and helioseismically inferred sound speed below solar convection zone (Gabriel 1997) when He diffusion included. – Direct helioseismic inversion for hydrogen abundance profile (Kosovichev 1995). 12/23/2021 26

Solar composition profiles near convection zone base including diffusion From Christensen-Dalsgaard et al. 2000 12/23/2021 27

Sound speed differences for solar models with/without diffusion and extra mixing No diffusion From Gabriel 1997 12/23/2021 28

Inversions to determine solar H abundance gradient From Kosovichev 1995 12/23/2021 29

Helioseismology Results ®Latest opacities and EOS give excellent results in comparisons between calculated and observed solar oscillation frequencies Guzik and Swenson 1997 Agreement is to within 0. 1%, but frequency observations are accurate to 0. 01%! 12/23/2021 30

Results for d Scuti stars ® Example: attempted detailed match to FG Vir – 29 observed frequencies 106 to 395 µHz ® Evolution models matching observational constraints (L, Teff, g, 140. 5 µHz mode = radial fundamental) nonunique ® No model found that matches all observed frequencies ® Frequency predictions are sensitive to – composition and gradients – extent of convective core and overshoot – rotation rate and differential rotation ® More modes predicted than observed (problem worse for more evolved d Sct stars) 12/23/2021 31

FG Vir Evolution Models Guzik et al. in Delta Scuti and related stars, ASP Vol. 210, 2000 12/23/2021 32

FG Vir Model Properties 1. 82 M (Z=0. 02) 1. 95 M (Z=0. 03) R (R ) M/R 3 Teff (K) 2. 26 0. 1575 7368 2. 31 0. 1580 7412 log g 3. 99 4. 00 log L/L 1. 13 1. 16 Xcc Rcc/R Mcc/M Age (Gyr) 0. 257 0. 155 0. 175 0. 879 0. 345 0. 181 0. 220 0. 731 12/23/2021 33

1. 82 M model frequencies vs. 1. 95 M model frequencies Guzik et al. in Delta Scuti and related stars, ASP Vol. 210, 2000 12/23/2021 34

Observed and calculated FG Vir frequencies (observations from Breger et al. 1997) 12/23/2021 35