Using Plane Parallax to Calibrate Dense Camera Arrays

Using Plane + Parallax to Calibrate Dense Camera Arrays Vaibhav Vaish, Bennett Wilburn, Neel Joshi, Marc Levoy Computer Science Department Stanford University Ó 2004 Marc Levoy

The Stanford Multi-Camera Array Ó 2004 Marc Levoy

Synthetic Aperture Photography: Seeing through Foliage Ó 2004 Marc Levoy

Outline • Problem Statement – Synthetic aperture photography using an array of cameras – Calibration required • Calibration Pipeline • Results • Future Work Ó 2004 Marc Levoy

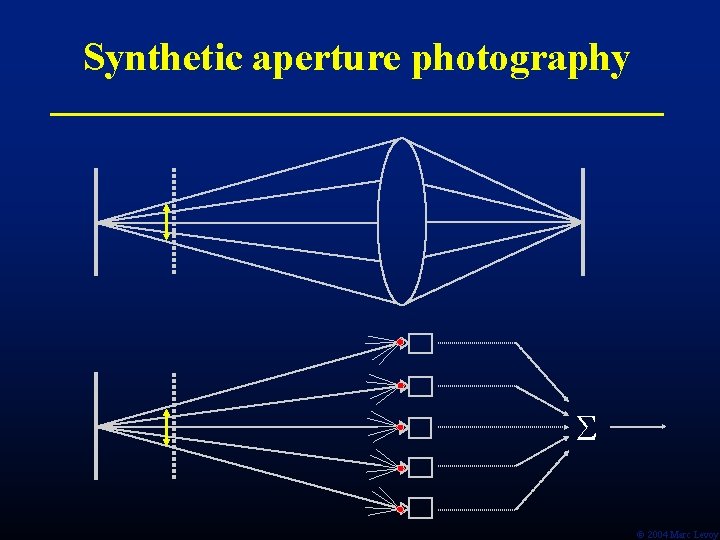
Synthetic aperture photography Ó 2004 Marc Levoy

SAP: Prior Work • Synthetic Aperture Radar • Light Field Rendering [Levoy 96] • Dynamically Reparametrized Light Fields [Isaksen 00] • Single lens SAP [Favaro 03] Ó 2004 Marc Levoy

Outdoor SAP: Array layout • • width of aperture number of cameras spacing between cameras camera’s field of view 2 m 45 13 cm 4. 5° Ó 2004 Marc Levoy

Outdoor SAP: The scene • distance to occluder • distance to targets • field of view at target 33 m 45 m 3 m Ó 2004 Marc Levoy

Outdoor SAP: Calibration Volume Focal Depth a = 2 m 28 m 5 m 12 m • Narrow field of view and long-range imaging makes accurate pose estimation difficult • Cannot take calibration measurements at the desired focal depth (behind occluding bushes) Ó 2004 Marc Levoy

Calibration Goal Focal Plane Given a focal plane, compute the projective transform (homography) to project each camera image onto the plane. Ó 2004 Marc Levoy

Approaches to Calibration • Metric Calibration – Computes camera intrinsics, position, orientation (10 parameters/camera) – Nonlinear optimization, requires initial guess – Not stable for narrow angle lenses and long range imaging • Non-metric Calibration – Plane + Parallax methods [Irani 96, Triggs 00] – Homography Spaces [Zelnik-Manor 99] Ó 2004 Marc Levoy

Calibration Pipeline • Problem Statement • Calibration Pipeline – Focus cameras on one plane (using homographies) – Compute relative camera positions from parallax measurements – Use camera positions to vary focal plane over a range of depths • Results • Future Work Ó 2004 Marc Levoy

Focusing on one plane Add camera images so that points on one plane are in good focus + Ó 2004 Marc Levoy

Focusing at different depths + Ó 2004 Marc Levoy

Focusing at different depths To focus at a different depth, we have to shift the images by an amount equal to the parallax + Ó 2004 Marc Levoy

Parallax and Camera Geometry P z p P 1 Reference Plane Z 0 X 1 Camera Plane p 1= X 1. z/(Z 0 + z) = X 1. d. P Parallax = Camera shift * Relative Depth Ó 2004 Marc Levoy

Parallax and Camera Geometry P p 1 X 1 Reference Plane p 2 X 2 Camera Plane Measure parallax of P in all cameras (wrt reference camera) [ p 1 p 2. . . ]T Ó 2004 Marc Levoy

Recovering Camera Positions Parallax of point P: For multiple points P 1, … Pn : Relative camera positions Xi can be recovered robustly (up to scale) using SVD. Ó 2004 Marc Levoy

Computing SAP Images at different focal depths p 1 X 1 • To change the focal depth, images have to be shifted by the amount of parallax. • In camera C 1 , the parallax for a parallel focal plane is f. X 1 , where f is a constant that depends only on the depth of the plane. • f is analogous to the focus distance of the synthetic lens: varying f changes the depth of the focal plane. Ó 2004 Marc Levoy

Algorithm for SAP 1. Focus cameras onto a frontoparallel plane 2. Compute parallax for one (or more) scene points 3. Recover relative camera positions Xi (up to an unknown scale) 4. For a range of values of f : 1. 2. Shift image from camera Ci by f. Xi and average shifted images. Varying f corresponds to changing the focus Ó 2004 Marc Levoy

Results Synthetic Aperture Sequence Ó 2004 Marc Levoy

Parallax v/s Metric Calibration Parallax-based calibration Metric calibration Ó 2004 Marc Levoy

Summary • Calibration of camera arrays for synthetic aperture photography – – Decompose warps into reference homography and shifts Use parallax measurements to compute camera positions Avoids computing camera intrinsics and orientation explicitly Robust, linear solution • Metric information not available • Algorithm requires planar camera array and frontoparallel reference plane Ó 2004 Marc Levoy

Extension : Tilted Focal Planes Reference Plane Focal Plane L (line of intersection) e (epipole) - Parallax is described by a projective warp (not a shift) - Rank-1 factorization is still possible Ó 2004 Marc Levoy

Future Work • Real-time applications – Warp images in hardware – Track moving objects by moving focal plane • 3 D Reconstruction from synthetic focus – Is this more robust to occlusions ? • Quantitative analysis of synthetic aperture photography – Effect of occluder density, number of cameras, aperture shape Ó 2004 Marc Levoy

Acknowledgements • Sponsors – NSF IIS-0219856 -001 – DARPA NBCH 1030009 • Assistance in acquisition – Gaurav Garg, Augusto Roman, Billy Chen, Pradeep Sen, Doantam Phan, Guillaume Poncin, Jeff Klingner High Speed Videography Using a Dense Camera Array B Wilburn, N Joshi, V Vaish, M Levoy, M Horowitz Session 5 A, 4: 20 pm Ó 2004 Marc Levoy