Using Percent Equations What you will learn Solve

Using Percent Equations What you will learn: Solve percent problems using percent equations Solve real-life problems involving discount and interest

Vocabulary £ Percent Equation : an equivalent form of the percent proportion in which the percent is written as a decimal £ Discount : the amount by which the regular price of an item is reduced £ Simple Interest : the amount of money paid or earned for the use of money

The Percent Equation Part = Percent <----The percent is Base written as a decimal Part Base = Percent Base Multiply each side by the base Part = Percent Base <-----this is the percent equation

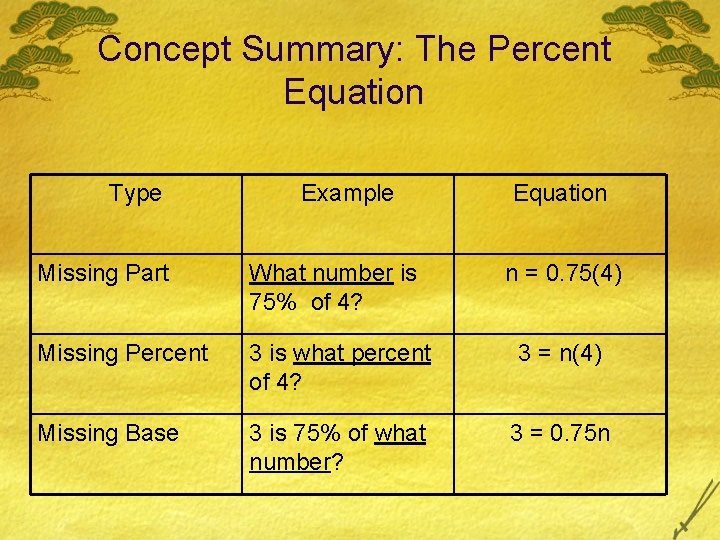
Concept Summary: The Percent Equation Type Example Equation Missing Part What number is 75% of 4? n = 0. 75(4) Missing Percent 3 is what percent of 4? 3 = n(4) Missing Base 3 is 75% of what number? 3 = 0. 75 n

Example 1: Find the Part £Find 42% of 150 You know the base is 150 and the percent is 42%. Let n represent the part. n = 0. 42(150) Write 42% as the decimal 0. 42 n = 63 Simplify So, 42% of 150 is 63. Is that reasonable? Yes because you know that 75 is 50% of 150, so 42% should be less than half.

Example 2: Find the Percent 37. 5 is what percent of 30? You know that the base is 30 and the part is 37. 5. Let n represent the percent. Part = Percent Base 37. 5 = n(30) 30 30 Divide each side by 30 1. 25 = n Move the decimal 2 places left to change into a % So, 37. 5 is 125% of 30

Example 3: Find the Base 83. 5 is 125% of what number? You know that the part is 83. 5 and the percent Is 125. Let n represent the base. Part = Percent Base 83. 5 = 1. 25 n 1. 25 Remember, using the percent equation, the percent is turned to a decimal. 66. 8 = n So, 83. 5 is 125% of 66. 8

The percent equation can also be used to solve problems involving discount and interest. £Example 4: Find Discount A frozen pizza is on sale at a 25% discount. Find the sale price of the pizza if it normally sells for $4. 85 Method 1: First use the percent equation to find 25% of $4. 85 Let D = the discount Part = Percent Base D =. 25(4. 85) D = 1. 2125 Since this is money, round to the nearest hundredth D = 1. 21 Then find the sale price: $4. 85 - $1. 21 = $3. 64

A frozen pizza is on sale at a 25% discount. Find the sale price of the pizza if it normally sells for $4. 85 Method 2: A discount of 25% means the item will cost 100% - 25% or 75% of the original price. Use the percent equation to find 75% of $4. 85 Let s represent the sale price. S = 0. 75(4. 85) S = 3. 6375 Remember, dealing with $$ so round to nearest hundredth! The sale price of the pizza will be $3. 64

Simple Interest Use the following formula: Annual Interest Rate (as a decimal) Interest------> I = prt <----- Time (in years) principal (amt. of $$ invested/ borrowed)

Example 5: Apply Simple Interest Formula I= prt What is the annual interest rate if $1600 is invested for 6 years and $456 in interest is earned? Fill in the formula! 456 = 1600 r 6 456 = 9600 r 9600 R =. 0475 Turn the decimal into a percent So, the interest rate is 4. 75%

Your Turn! Solve each problem using the percent equation. part = Percent base A. 12 is what percent of 400? 12= P 400 P=. 03 move the decimal to make it a % 3% B. What is 20% of 110? p =. 20(110) p = 22 C. 30 is 60% of what number? 30 =. 60 b 50 = b

2 More! A jacket that normally sells for $180 is on sale at a 35% discount. What is the sale price of the jacket? D =. 35(180) D = 63 $180 -$63 = $117 How long will it take to earn $252 in interest if $2400 is invested at a 7% annual interest rate? I = prt 252= 2400(. 07)t 252=168 t 1. 5 = t It will take 1. 5 years