Using Pattern Recognition Techniques to Derive a Formal

Using Pattern Recognition Techniques to Derive a Formal Analysis of Why Heuristic Functions Work B. John Oommen A Joint Work with Luis G. Rueda School of Computer Science Carleton University March 7, 2002 1

Optimization Problems Any arbitrary optimization problem: • Instances, drawn from a finite set, X, • An Objective function • Some feasibility functions The aim: • Find an (hopefully the unique) instance of X, • which leads to a maximum (or minimum) • subject to the feasibility constraints. March 7, 2002 2

An Example The Traveling Salesman Problem (TSP) • Consider the cities numbered from 1 to n, • The salesman starts from city 1, • visits every city once, and • Returns to city 1. An instance of X is a permutation of cities: For example, 1 4 3 2 5, if five cities considered The objective function: • The sum of the inter-city distances: • 1 4, 4 3, 3 2, 2 5, 5 1 March 7, 2002 3

Heuristic Functions A Heuristic algorithm is an algorithm which attempts to find a certain instance X that maximizes the objective function It iteratively invokes a Heuristic function. The heuristic function estimates (or measures) the cost of the solution. The heuristic itself is a method that performs one or more changes to the current instance. March 7, 2002 4

An Open Problem Consider a Heuristic algorithm that invokes any of Two Heuristic Functions : H 1 and H 2 used in estimating the solution to an Optimization problem If Estimation accuracy of H 1 > Estimation accuracy of H 2 Does it imply that H 1 has higher probability of leading to the optimal QEP? March 7, 2002 5

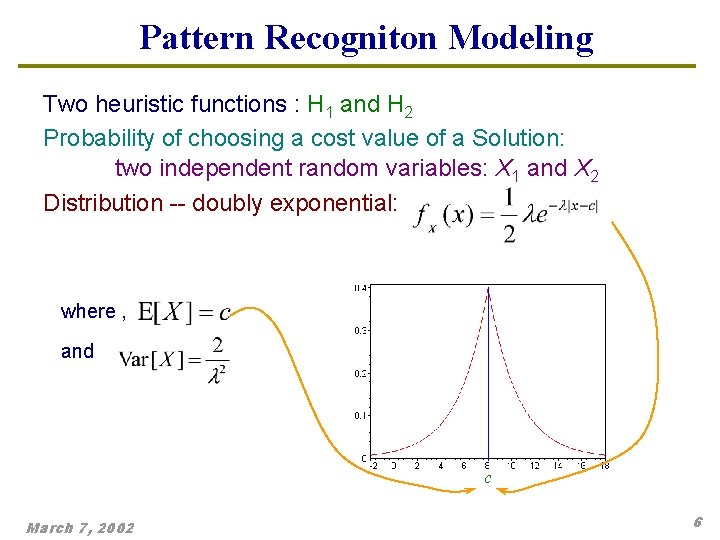
Pattern Recogniton Modeling Two heuristic functions : H 1 and H 2 Probability of choosing a cost value of a Solution: two independent random variables: X 1 and X 2 Distribution -- doubly exponential: where , and c March 7, 2002 6

Pattern Recogniton Modeling Our model: Error function is doubly exponential. Typical in reliability analysis and failure models. How reliable is a Solution when only estimate known? Assumptions: Mean cost of Optimal Solution: , then shift the origin by E[X] = 0 Variances: Estimate X 1 better than Estimate of X 2 March 7, 2002 7

Main Result (Exponential) ü H 1 and H 2, two heuristic functions. ü X 1 and X 2, two r. v. optimal solution obtained by H 1 and H 2 ü X 1’ and X 2’, other two r. v. for sub-optimal solution ü Let p 1 and p 2 the prob. that H 1 and H 2 respectively make the wrong decision. Shown that: then : March 7, 2002 8

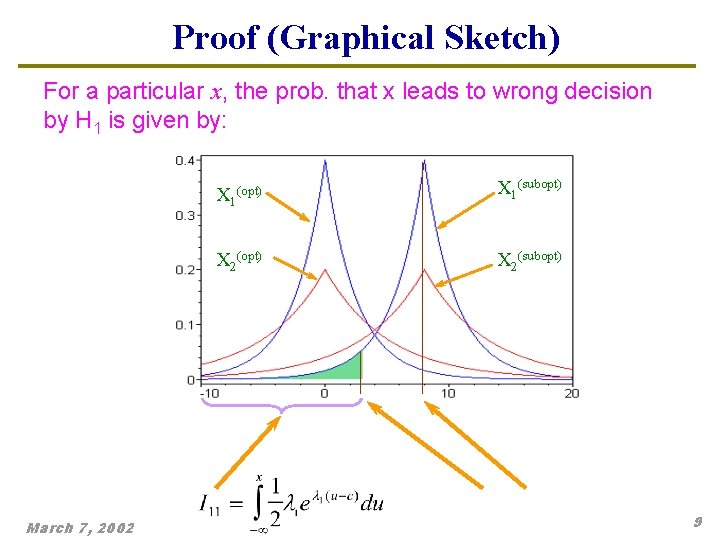
Proof (Graphical Sketch) For a particular x, the prob. that x leads to wrong decision by H 1 is given by: March 7, 2002 X 1(opt) X 1(subopt) X 2(subopt) 9

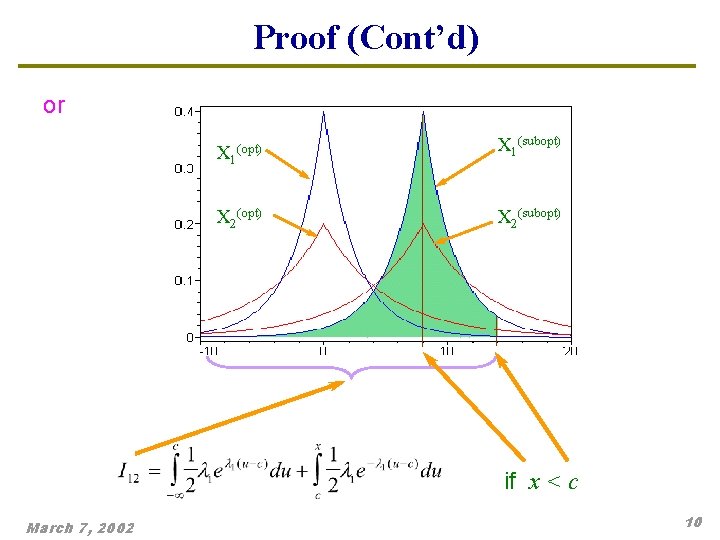
Proof (Cont’d) or X 1(opt) X 1(subopt) X 2(subopt) if x < c March 7, 2002 10

Proof (Cont’d) The total probability that H 1 makes the wrong decision for all values of x is: Similarly, the prob. that H 2 makes the wrong decision for all values of x is: March 7, 2002 11

Proof (Cont’d) Solving integrals and making p 1 p 2, we have: which, using ln x x - 1, implies that p 1 p 2 QED where 1 = 1 c and 2 = 2 c Also 2 substituted for k 1 March 7, 2002 12

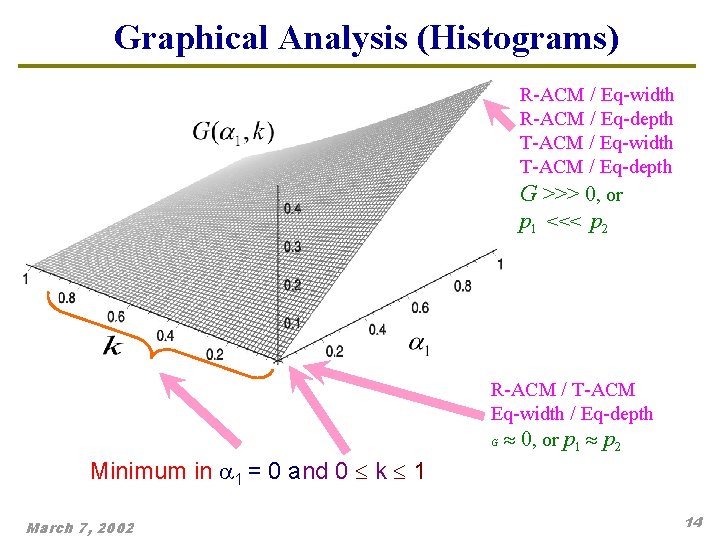
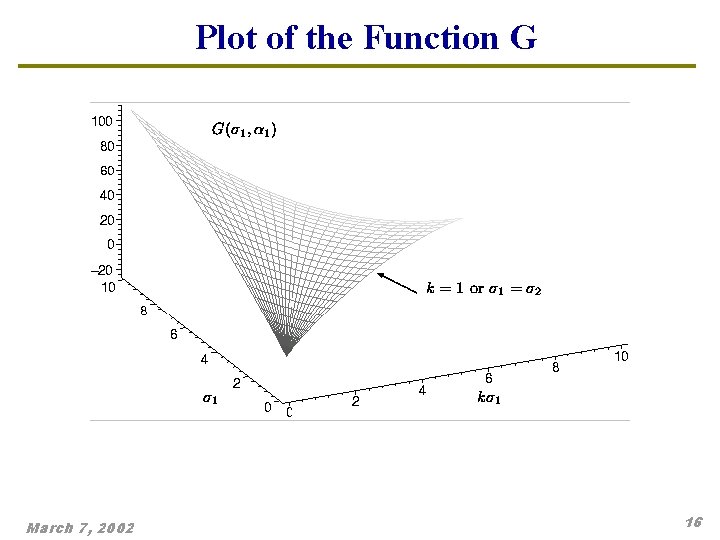
Second Theorem F( 1, k) can also be written in terms of 1 and k as: Suppose that 1 0 and 0 k 1, then G( 1, k) 0, and there are two solutions for G( 1, k) = 0 and Proof: Taking partial derivatives and solving: and March 7, 2002 13

Graphical Analysis (Histograms) R-ACM / Eq-width R-ACM / Eq-depth T-ACM / Eq-width T-ACM / Eq-depth G >>> 0, or p 1 <<< p 2 R-ACM / T-ACM Eq-width / Eq-depth G 0, or p 1 p 2 Minimum in 1 = 0 and 0 k 1 March 7, 2002 14

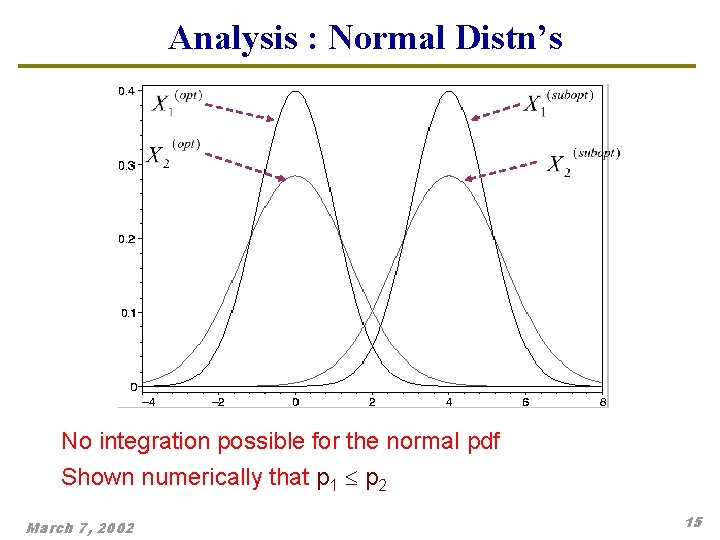
Analysis : Normal Distn’s No integration possible for the normal pdf Shown numerically that p 1 p 2 March 7, 2002 15

Plot of the Function G March 7, 2002 16

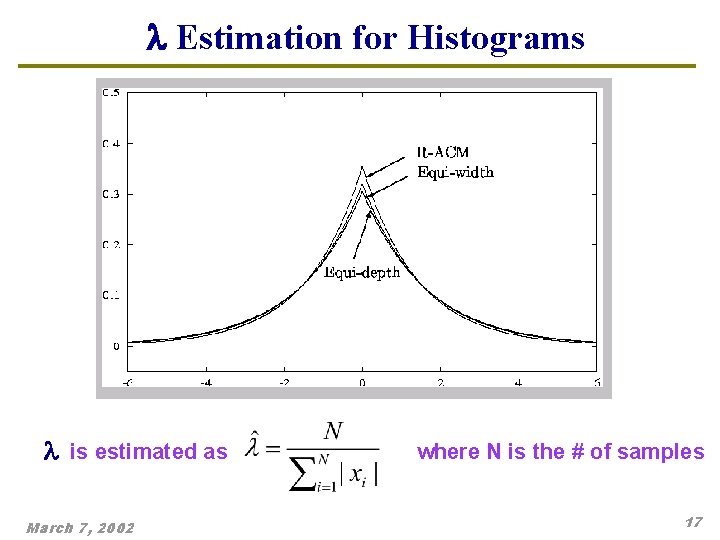
l Estimation for Histograms l is estimated as March 7, 2002 where N is the # of samples 17

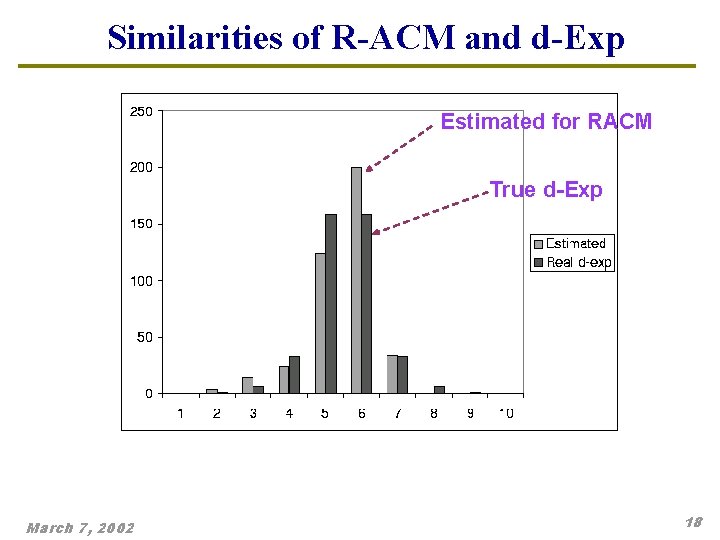
Similarities of R-ACM and d-Exp Estimated for RACM True d-Exp March 7, 2002 18

Simulations Details Simulations performed in Query Optimization: ü 4 independent runs per simulation. ü 100 random Databases per run 400 per simulation. ü 6 Relations, ü 6 Attributes per relation, ü 100 tuples per relation. Four independent runs on 100 databases: R-ACM vs. Traditional using: 11 bins, 50 values March 7, 2002 19

Empirical Results # of times in which R-ACM yields better QEP March 7, 2002 # of times in which Eq-width yields better QEP # of times in which Eq-depth yields better QEP 20

Conclusions ü Applied PR Techniques to solve problem of relating Heuristic Function Accuracy and Solution Optimality ü Used a reasonable model of accuracy (doubly exponential distribution). ü Shown analytically how the high accuracy of heuristic function leads to a superior solutions. ü Numerically shown the results for normal distributions ü Shown that R-ACM yield better QEPs in a larger number of times than Equi-width and Equi-depth. ü Empirical results on randomly generated databases also shown the superiority of R-ACM. ü Graphically demonstrated the validity of our model. March 7, 2002 21