Using Nondeterminism to Amplify Hardness Emanuele Viola Joint

Using Nondeterminism to Amplify Hardness Emanuele Viola Joint work with: Alex Healy and Harvard University Salil Vadhan

Average-Case Hardness of NP • Study hardness of NP on random instances – Natural question, essential for cryptography • One Goal: relate worst-case & avg-case hardness – Done for #P, PSPACE, EXP. . . [L 89, BF 90, BFL 91, . . . ] – New techniques needed for NP [FF 91, BT 03, V 04] • This Talk: hardness amplification – Relate mild avg-case & strong avg-case hardness

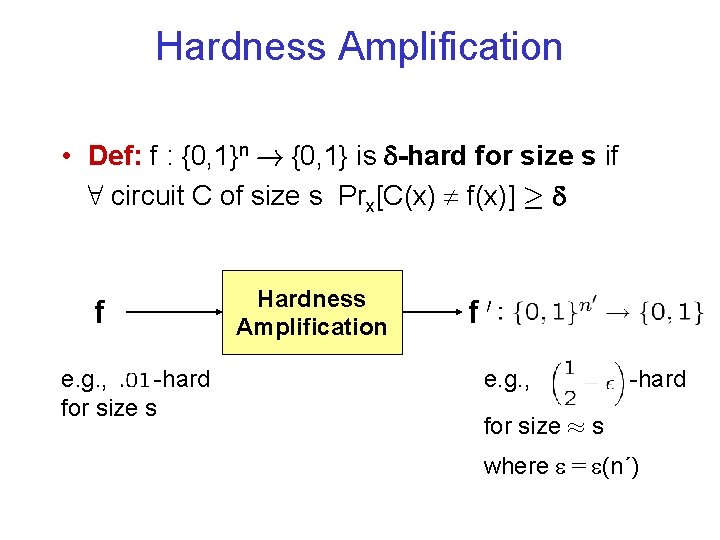
Hardness Amplification • Def: f : {0, 1}n ! {0, 1} is -hard for size s if 8 circuit C of size s Prx[C(x) f(x)] ¸ f e. g. , -hard for size s Hardness Amplification f 0 e. g. , -hard for size ¼ s where = (n´)

Standard Hardness Amplification • Yao’s XOR Lemma: f : {0, 1}n ! {0, 1} -hard for size s = s(n) ) f 0(x 1, . . . , xk) = f(x 1) ©. . . © f(xk) • k = n ) n´ = n 2 and f 0 : {0, 1}n' ! {0, 1} • ¼ Optimal, but cannot use in NP: f 2 NP ; f 0 2 NP

O’Donnell’s Amplification in NP • Idea: f´(x 1, . . . , xk) = C(f(x 1), . . . , f(xk)), C monotone • e. g. f(x 1) Æ ( f(x 2) Ç f(x 3) ). Then f´ 2 NP if f 2 NP • Theorem [O’Donnell `02]: 9 balanced f 2 NP (1/poly(n))-hard for size n (1) ) 9 f´ 2 NP -hard for size (n´) (1) • Barrier: No such construction can amplify above

Our Main Result Thm: 9 balanced f 2 NP (1/poly(n))-hard for size s(n) ) 9 f´ 2 NP ¼ -hard for size ¼ Examples: – s(n) = n (1) ) hardness – s(n) = W(1) n 2 ) hardness – s(n) = 2 W(n) ) hardness

Approach • Obs: Hardness of f´(x 1, . . . , xk) = C(f(x 1), . . . , f(xk)) limited by • Idea 1: Derandomization [I 95, IW 97] f´( ) = C(f(x 1), . . . , f(xk)) , where (x 1, . . . , xk) = G( ) for “pseudorandom” generator G, so • E. g. if then hope f´ • Q: Why does this still amplify hardness? – We exhibit unconditional G s. t. this works -hard

Approach (cont. ) f´( ) = C(f(x 1), . . . , f(xk)) , where (x 1, . . . , xk) = G( ) • Q: How to compute f´ 2 NP when k = (n´) (1)? • Idea 2: Nondeterminism – Use C s. t. C(f(x 1), . . . , f(xk)) can be computed nondeterministically looking at only log(k) f(xi )’s. – So f´ 2 NP even when k = 2 n’

Derandomizing Yao’s XOR Lemma • f -hard ¼ f 0 coin-flip 1 [ I 95 ] • f 0(x 1, . . . , xk) = f(x 1) ©. . . © f(xk) is coin-flip (i. e. hard) if some xi is a coin-flip happens w. h. p. over (x 1, . . . , xk) • Derandomize [IW 97]: Let (x 1, . . . , xk) = Expander. Walk( ) w. h. p. over , some xi is a coin-flip

Derandomizing O’Donnell’s proof • f -hard ¼ f 0 coin-flip 1 [ I 95 ] • f 0(x 1, . . . , xk) = C(f(x 1), . . . , f(xk)) coin-flip w. h. p. – Proof relies on noise sensitivity of C • Derandomize: – If G fools C(f(¢), . . . , f(¢)), then f 0( ) = C(f(x 1), . . . , f(xk)) is coin-flip w. h. p. over – C(f(¢), . . . , f(¢)) computable in small space (n + log k) – Use Nisan (‘ 92) PRG for small space algorithms

The structure of C C = TRIBES MONOTONE DNF [BL 90] Claim: If f 2 NP then f´ 2 NP even for k = 2 Proof: To compute f´( ): – Guess a clause, say (f(xi+1) Æ. . . Æ f(xi+b)) – Check if clause is true n´

Conclusion • O’Donnell’s hardness amplification in NP: – – Amplifies up to No construction of same form does better • Our result: amplify up to • Two new techniques: 1. Derandomization 2. Nondeterminism • G fools C(f(¢), . . . , f(¢)) k = n (1) Only obstacle to hardness is PRG with logarithmic seed length for space or const-depth