Using Neumann Series to Solve Inverse Problems in

Using Neumann Series to Solve Inverse Problems in Imaging Christopher Kumar Anand

Inverse Problem Solve for • given • measurements ( • model ( ) 2 . ) Anand-Neumann Series-Adv. Ol-Feb 2007

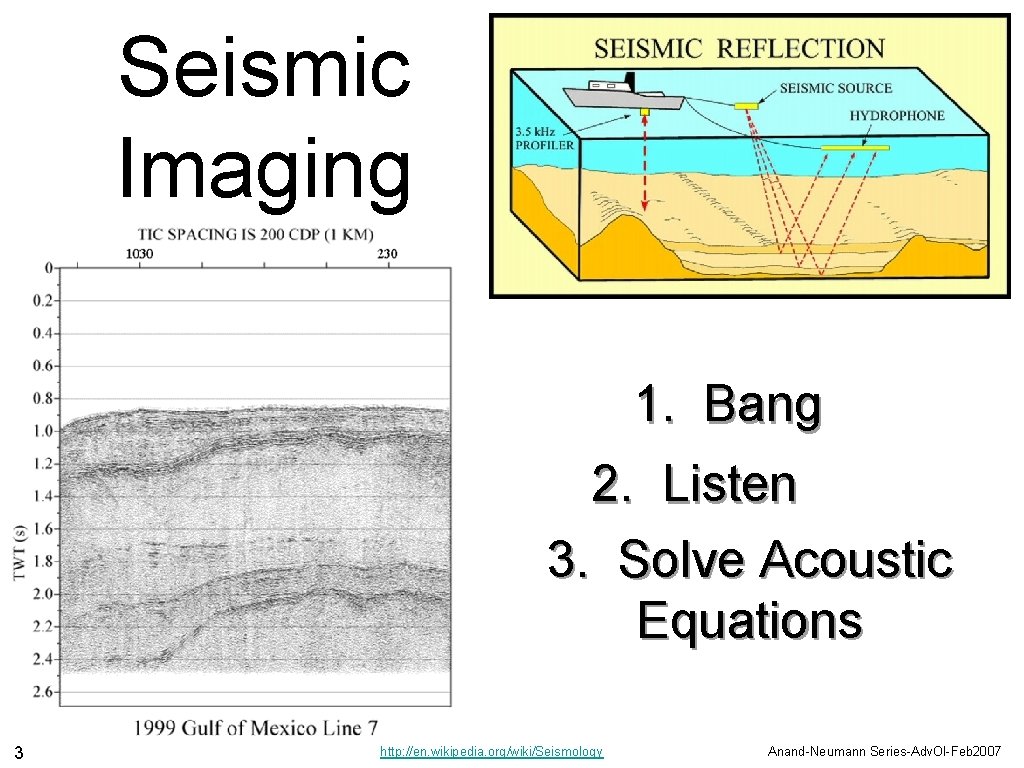
Seismic Imaging 1. Bang 2. Listen 3. Solve Acoustic Equations 3 http: //en. wikipedia. org/wiki/Seismology Anand-Neumann Series-Adv. Ol-Feb 2007

Magnetic Resonance Imaging 0. Tissue Density 1. Phase Modulation 2. Sample Fourier Transform 3. Invert Linear System 4 Anand-Neumann Series-Adv. Ol-Feb 2007

Challenging when. . . • model is big • 1 000 000 variables • model is nonlinear • data is inexact (usually know error probabilistically) 5 Anand-Neumann Series-Adv. Ol-Feb 2007

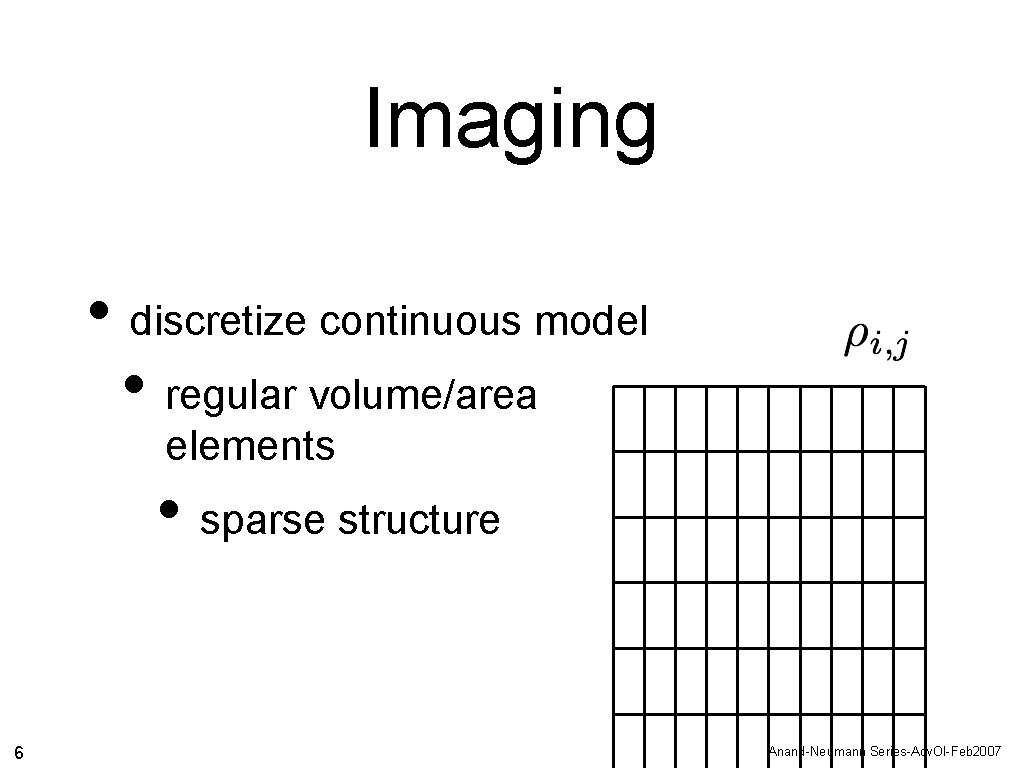
Imaging • discretize continuous model • regular volume/area elements • sparse structure 6 Anand-Neumann Series-Adv. Ol-Feb 2007

Solutions: Noise • filter noisy solution • 7 1. convolution filter 2. bilateral filter 3. Anisotropic Diffusion (uses pde) regularize via penalty 4. energy 5. Total Variation 6. something new Anand-Neumann Series-Adv. Ol-Feb 2007

Solutions: Problem Size I. use a fast method (i. e. based on FFT) II. use (parallelizable) iterative method a. Conjugate Gradient b. Neumann series III. use sparsity c. choose penalties with sparse Hessians IV. use fast hardware d. 1000 -way parallelizable I. single precision 8 Anand-Neumann Series-Adv. Ol-Feb 2007

Cell BE • 25 GFlops DP • 200 GFlops SP • need 384 -way ||ism • • 9 4 -way SIMD 8 -way cores 6 -times unrolling double buffering Anand-Neumann Series-Adv. Ol-Feb 2007

Solutions: Nonlinearity use iterative method A. sequential projection onto convex sets B. trust region C. sequential quadratic approximations 10 Anand-Neumann Series-Adv. Ol-Feb 2007

Plan of Talk 11 A. example/benchmark B. optimization 1. fit to data 2. regularization i. new penalty (with optimized gradient) ii. nonlinear penalties C. solution 3. operator decomposition A. Neumann series B. proof of convergence 1. numerical example 2. noise reduction i. linear convergence Anand-Neumann Series-Adv. Ol-Feb 2007

Example/Benchmark complex image complex data 12 model Anand-Neumann Series-Adv. Ol-Feb 2007

Example/Benchmark diagonal blocks easily invertible 13 Anand-Neumann Series-Adv. Ol-Feb 2007

Example/Benchmark direct inverse 14 Anand-Neumann Series-Adv. Ol-Feb 2007

Optimization fit-to-data quadratic penalties 15 nonlinear penalties Anand-Neumann Series-Adv. Ol-Feb 2007

Fit to Data • typically dense transformation • use fast matrix-vector products • e. g. FFT-based forward/adjoint problem • linear forward problem gives quadratic 16 objective Anand-Neumann Series-Adv. Ol-Feb 2007

Bilateral Filter spatial range kernel Bilateral Regularizer 17 Anand-Neumann Series-Adv. Ol-Feb 2007

Quadtratic Case • optimize direction of gradient • LP problem like FIR filter design • heuristic choice of “stop band” 18 Anand-Neumann Series-Adv. Ol-Feb 2007

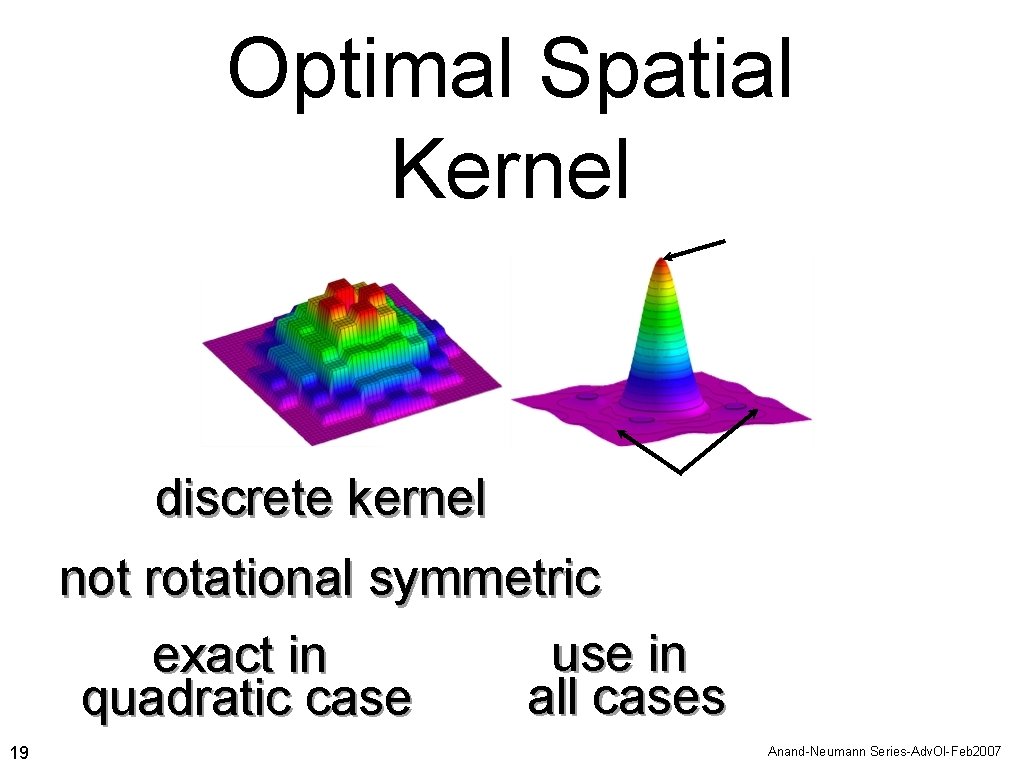
Optimal Spatial Kernel discrete kernel not rotational symmetric use in exact in all cases quadratic case 19 Anand-Neumann Series-Adv. Ol-Feb 2007

TV-like • similar properties to Total Variation • won’t smooth edges • not differentiable 20 Anand-Neumann Series-Adv. Ol-Feb 2007

Sequential Quadratic TV-like • sequential quadratic approximation • tangent to TV-like 21 Anand-Neumann Series-Adv. Ol-Feb 2007

Mask • penalize pixel values outside object 22 Anand-Neumann Series-Adv. Ol-Feb 2007

Segmentation • probability of observing pixels • assumes discrete pixel values • equal likelihood • equal normal error 23 Anand-Neumann Series-Adv. Ol-Feb 2007

Solve: Operator Decomposition “small” • block diagonal with sparse banded blocks • linear-time Cholesky decomposition e • leads to formal expression 24 g a im ws o = r s k c o l b Anand-Neumann Series-Adv. Ol-Feb 2007

Calculate Using Fast Matrix-Vector Ops linear in problem size 25 plus (poly-order)(fast algorithm) Anand-Neumann Series-Adv. Ol-Feb 2007

Row by Row • each block corresponds to a row • each block can be calculated in parallel • (number-rows)-way parallelism 26 Anand-Neumann Series-Adv. Ol-Feb 2007

Even Better: Use Minimax Polynomial • calculate 27 Anand-Neumann Series-Adv. Ol-Feb 2007

Convergence next error minimax current error step polynomial shortening error 28 Anand-Neumann Series-Adv. Ol-Feb 2007

Safe in Single. Precision • recalculate gradient at each outer iteration • numerical error only builds up during polynomial evaluation • coefficients well-behaved (and in our control) 29 Anand-Neumann Series-Adv. Ol-Feb 2007

Numerical Tests • start with quadratic penalties • add nonlinear penalties and change weights • with and without time fixed budget for computation 30 Anand-Neumann Series-Adv. Ol-Feb 2007

10 iterations I. 10 iterations with bi 2 regularization 31 Anand-Neumann Series-Adv. Ol-Feb 2007

100 iterations I. 10 iterations with bi 2 regularization II. introduce other penalties 1. masking 2. magnet 3. segmentation 32 Anand-Neumann Series-Adv. Ol-Feb 2007

15 iterations optimized c simple c 33 Anand-Neumann Series-Adv. Ol-Feb 2007

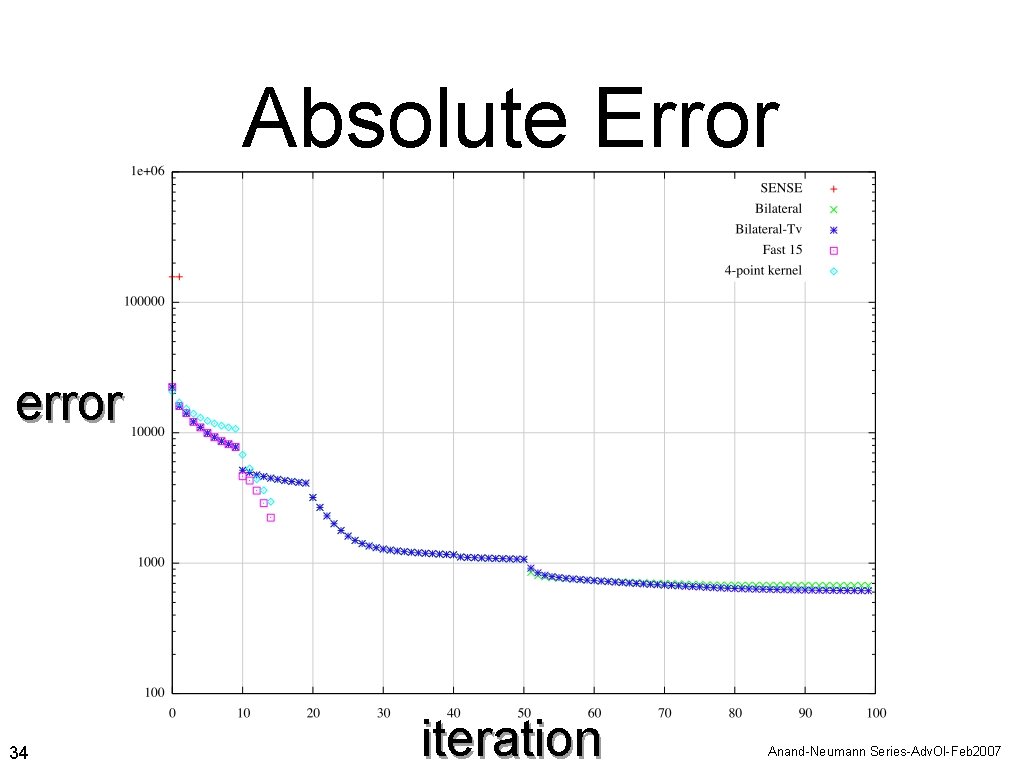
Absolute Error error 34 iteration Anand-Neumann Series-Adv. Ol-Feb 2007

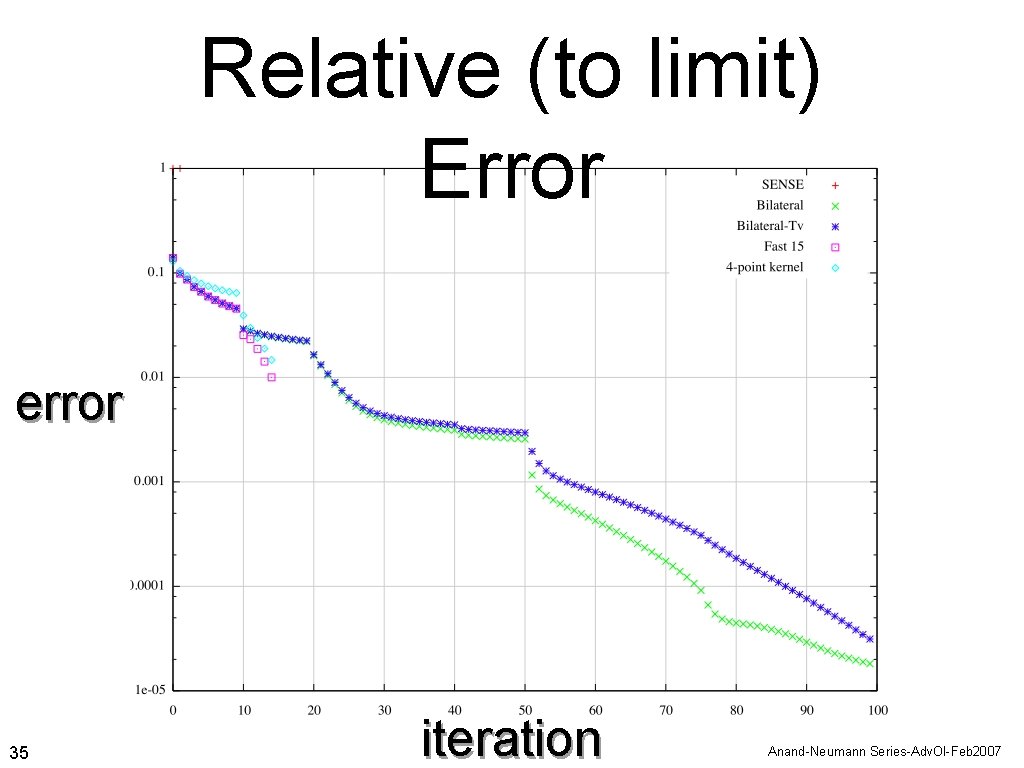
Relative (to limit) Error error 35 iteration Anand-Neumann Series-Adv. Ol-Feb 2007

Conclusion • highly-parallel • safe in single precision • robust with respect to noise • accommodates nonlinear penalties 36 Anand-Neumann Series-Adv. Ol-Feb 2007

Thanks to: students and colleagues in the of 37 Anand-Neumann Series-Adv. Ol-Feb 2007