Using MReps to include apriori Shape Knowledge into

Using M-Reps to include a-priori Shape Knowledge into the Mumford-Shah Segmentation Functional FWF - Forschungsschwerpunkt S 092 Subproject 7 „Pattern and 3 D Shape Recognition“ Grossauer Harald 1

Outlook • • Mumford-Shah with a-priori knowledge Medial axis and m-reps Statistical analysis of shapes 2

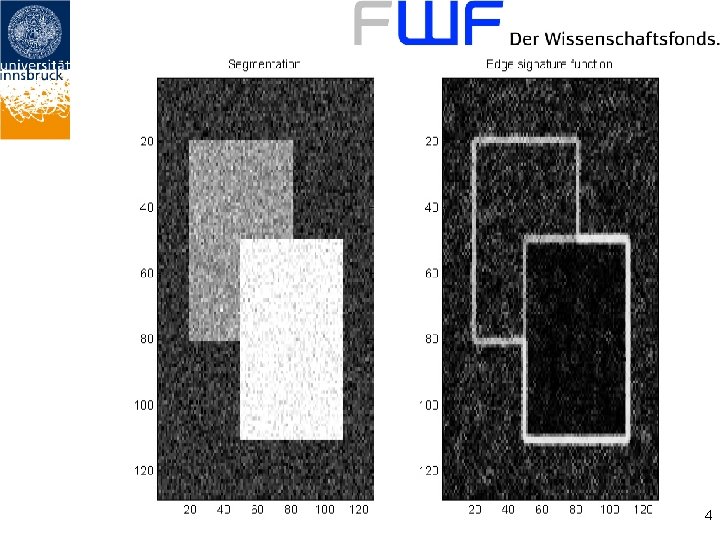
Mumford-Shah • Original Mumford-Shah functional: • For minimizers (u, C): – u … piecewise constant approximation of f – C … curve along which discontinuities of u are located 3

4

Mumford-Shah with a-priori knowledge • Replace by d(Sap, S) • Sap represents the expected shape (prior) • d(Sap, ∙) somehow measures the distance to the prior How is „somehow“? 5

Curve representation • Curves (resp. surfaces) are frequently represented as – Triangle mesh (easy to render) – Set of spline control points (smoother) – CSG, … • Problems: – Local boundary description – No global shape properties 6

Blum‘s Medial Axis (in 2 D) • Medial axis for a given „shape“ S: Set of centers of all circles that can be inscribed into S, which touch S at two or more points • Medial axis + radius function → Medial axis representation (m-reps) 7

Information derived from the m-rep (1) • Connection graph: – – Hierarchy of figure(s) Main figure, protrusion, intrusion Topology of surface Connection and substance edges 8

Information derived from the m-rep (2) • Let – – – be a parametrization of , then is the „principal direction“ of S describes the „bending“ of S is the local „thinning“ or „thickening“ of S – Branchings of may indicate singular surface points (edges, corners) 9

Problem of m-reps • Stability: • We never infer the medial axis from the boundary surface! 10

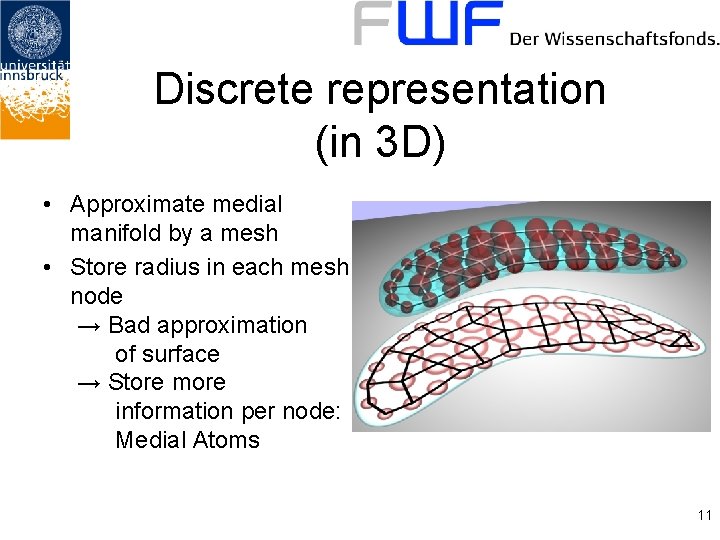
Discrete representation (in 3 D) • Approximate medial manifold by a mesh • Store radius in each mesh node → Bad approximation of surface → Store more information per node: Medial Atoms 11

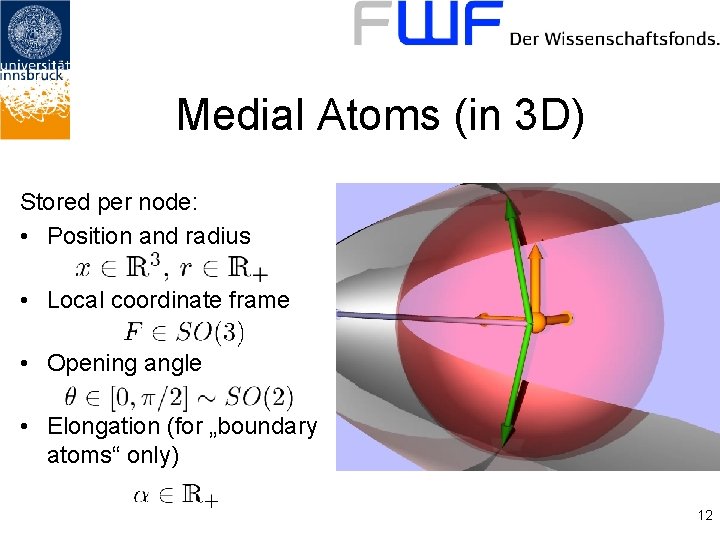
Medial Atoms (in 3 D) Stored per node: • Position and radius • Local coordinate frame • Opening angle • Elongation (for „boundary atoms“ only) 12

Shape description by medial atoms • One medial atom: • Shape consisting of N medial Atoms: + connection graph 13

A distance between shapes? • Current main problem: What is a suitable distance Or maybe even consider 14

Statistical analysis of shapes • Goal: Principal Component Analysis (PCA) of a set of shapes • Zero‘th principal component = mean value • Problem: is not a vector space 15

Statistical analysis of shapes • Variational formulation of mean value: • No vector space structure needed, but not necessarily unique → All Si must be in a „small enough neighborhood“ 16

PCA in • For data – – the k‘th principal component is defined inductively by: is orthogonal to the subspace • has codimension k • the variance of the data is maximal , where: projected onto • How to carry over these concepts from the vector space to the manifold ? 17

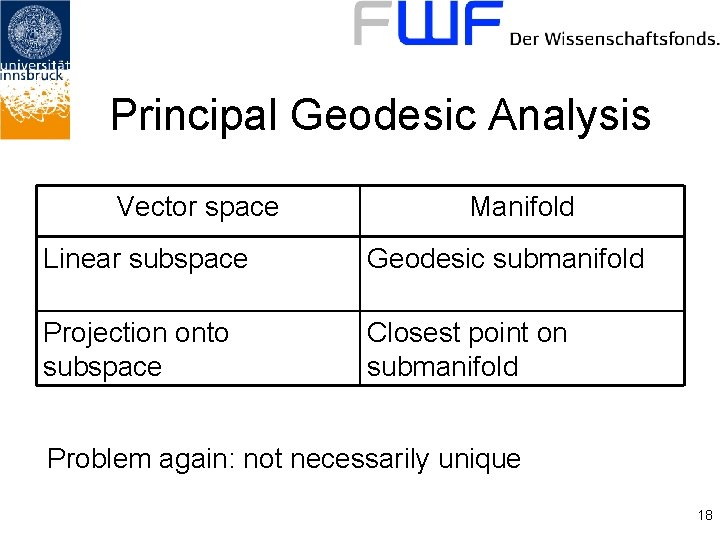
Principal Geodesic Analysis Vector space Manifold Linear subspace Geodesic submanifold Projection onto subspace Closest point on submanifold Problem again: not necessarily unique 18

Principal Geodesic Analysis • Second main problem(s): – Under what conditions is PGA meaningful? – How to deal with the non-uniqueness? – Does PGA capture shape variability well enough? – How to compute PGA efficiently? 19

The End Comments? Ideas? Questions? Suggestions? 20