Using Microsoft Excel to Conduct Regression Analysis Example

Using Microsoft Excel to Conduct Regression Analysis

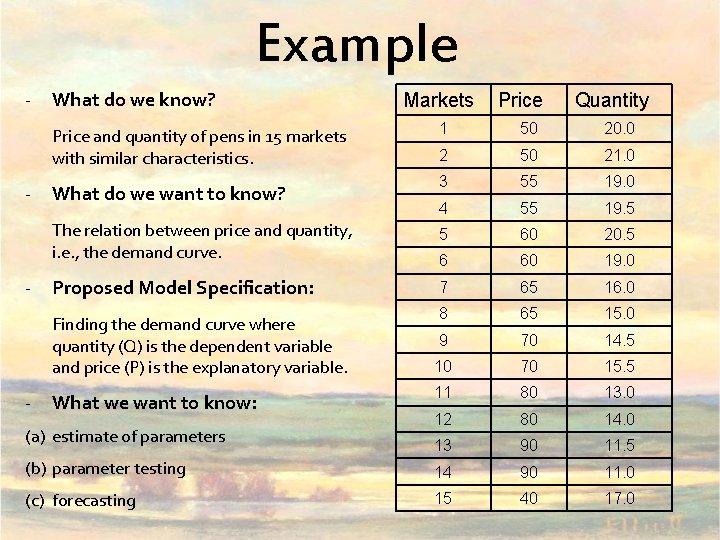
Example - What do we know? Markets Price Quantity 1 50 20. 0 2 50 21. 0 3 55 19. 0 4 55 19. 5 5 60 20. 5 6 60 19. 0 7 65 16. 0 8 65 15. 0 9 70 14. 5 10 70 15. 5 11 80 13. 0 12 80 14. 0 13 90 11. 5 (b) parameter testing 14 90 11. 0 (c) forecasting 15 40 17. 0 Price and quantity of pens in 15 markets with similar characteristics. - What do we want to know? The relation between price and quantity, i. e. , the demand curve. - Proposed Model Specification: Finding the demand curve where quantity (Q) is the dependent variable and price (P) is the explanatory variable. - What we want to know: (a) estimate of parameters

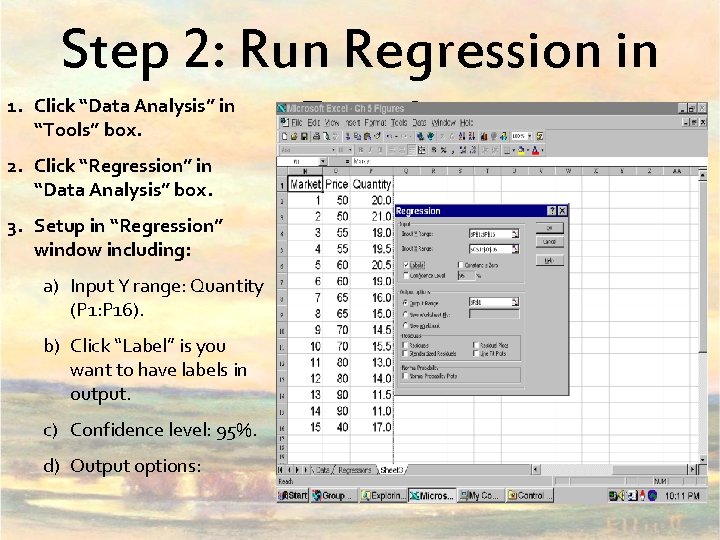
Step 2: Run Regression in Excel 1. Click “Data Analysis” in “Tools” box. 2. Click “Regression” in “Data Analysis” box. 3. Setup in “Regression” window including: a) Input Y range: Quantity (P 1: P 16). b) Click “Label” is you want to have labels in output. c) Confidence level: 95%. d) Output options:

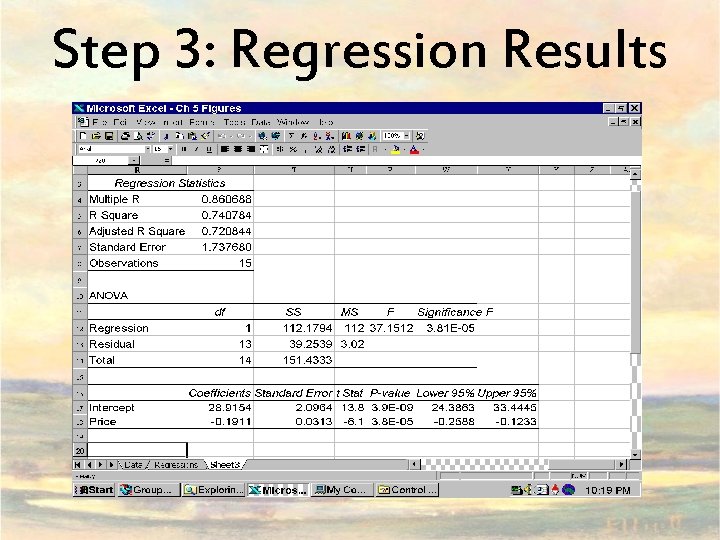
Step 3: Regression Results

Interpret Regression Output Estimated Linear Demand Function Intercept: Price coefficient: What proportion of variation of Y is explained by the regression? R² = 0. 74; Estimates of standard error: Estimates of variance: = 3. 02

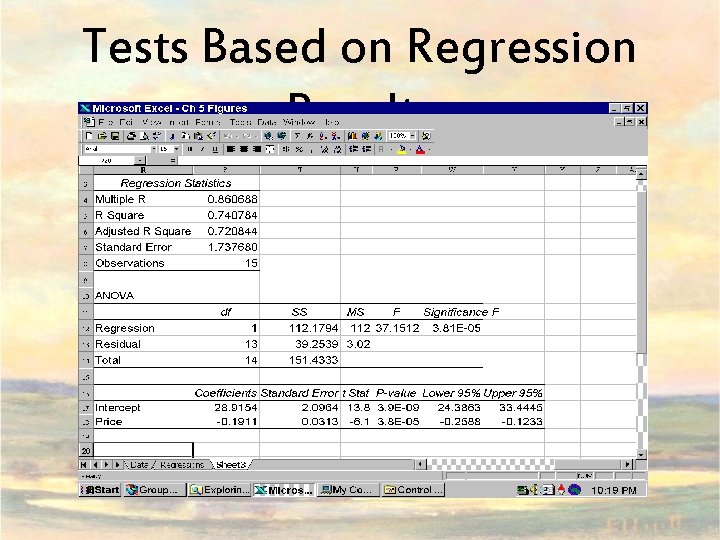
Tests Based on Regression Results

The t-Test Example: H 0: b = 0. 3 Step 1: Step 2: - Degrees of Freedom = 15 – 2 = 13, 2 -tailed test - One method: compare t-stat and c value t-stat: -3. 51 < -c = -2. 16 - Another method: finding out p-value p = tdist(3. 51, 13, 2) = 0. 00384 Step 3: - Reject the null hypothesis - Why? -3. 51 < -2. 16 or p = 0. 00384 < 0. 05

The t-Test Example: H 0: b > 0. 1 Step 1: Step 2: - DF = 15 – 2 = 13, 1 -tailed test, significant level 5% - One method: compare t-stat and c value t-stat: -2. 905 < -c = -t(0. 10, 13, 1, 5%) = -1. 771 - Another method: compare p-value and significant level p = tdist(2. 905, 13, 1) = 0. 006145 Step 3: - Reject the null hypothesis - Why? t = -2. 905 < -c = -1. 771 or p = 0. 006145 < 0. 05 stat

Confidence Interval of a = 28. 92 Calculate 95% CI of a = 28. 92 How? - CI of coefficient: - The critical value of c is 2. 16, given DF = 15 – 2 = 13, level of confidence = 5%, and two-tailed test. - se(estimate) = 2. 09 is the standard error of the estimate. Interpretation: - Any number outside of the CI is statistically different than the estimated a = 28. 92 - Any number within the CI is statistically no different than the estimated a = 28. 92

Confidence Interval: b = 0. 19 How? - CI of coefficient: - The critical value of c is 2. 16, given DF = 15 – 2 = 13, level of confidence = 5%, and two-tail. - se(estimate) = 0. 03 is the standard error of the estimate. Results: Interpretation: - Any number outside the CI is statistically different from -0. 19 at the 5% level. - Any number within the CI is statistically no different than the estimated b = -0. 19.