Using Mathematica for modeling simulation and property checking










































- Slides: 51

Using Mathematica for modeling, simulation and property checking of hardware systems Ghiath AL SAMMANE VDS group : Verification & Modeling of Digital systems TIMA Laboratory Techniques of Informatics and Microelectronics for computer Architecture © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 2 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 3 © Ghiath AL SAMMANE

What is TIMA ? (1) § Public research lab of the university of Grenoble and CNRS, located in the European equivalent to Silicon Valley § Carrying out research in the field of – Hardware design, architecture, test. – Verification & CAD tools. – Quality of integrated circuits and by means of data processing and microelectronics technology. § Transferring research results to industry § Contributing to knowledge dissemination by organizing conferences and editing journals 4 © Ghiath AL SAMMANE

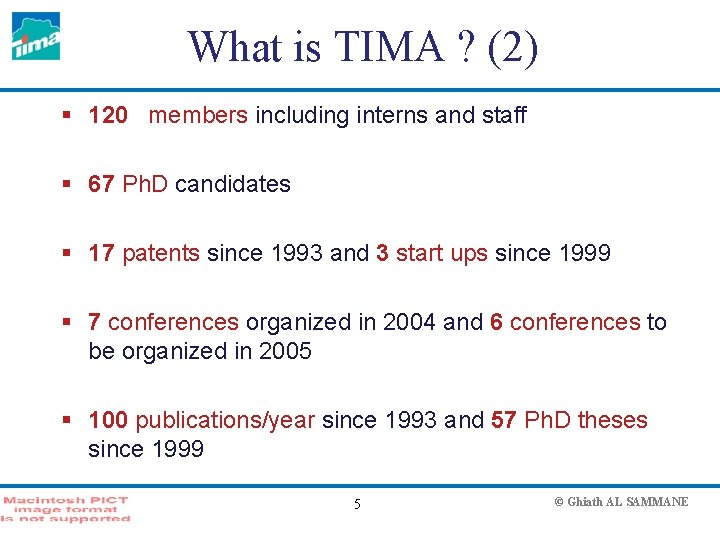
What is TIMA ? (2) § 120 members including interns and staff § 67 Ph. D candidates § 17 patents since 1993 and 3 start ups since 1999 § 7 conferences organized in 2004 and 6 conferences to be organized in 2005 § 100 publications/year since 1993 and 57 Ph. D theses since 1999 5 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 6 © Ghiath AL SAMMANE

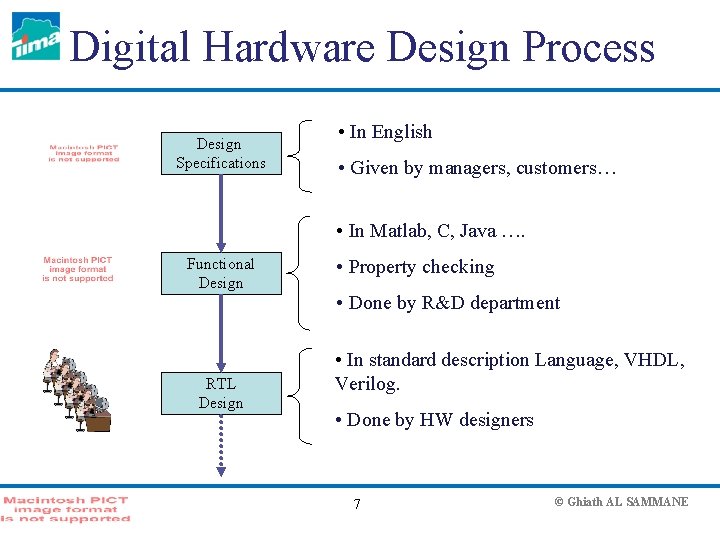
Digital Hardware Design Process Design Specifications • In English • Given by managers, customers… • In Matlab, C, Java …. Functional Design RTL Design • Property checking • Done by R&D department • In standard description Language, VHDL, Verilog. • Done by HW designers 7 © Ghiath AL SAMMANE

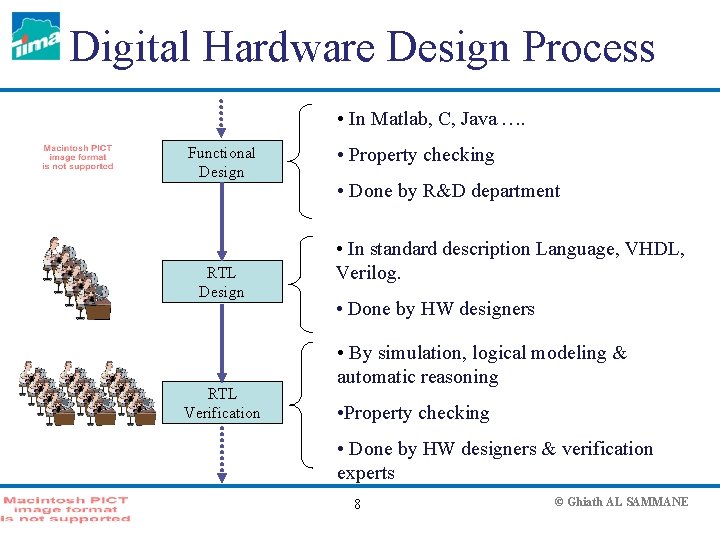
Digital Hardware Design Process • In Matlab, C, Java …. Functional Design RTL Verification • Property checking • Done by R&D department • In standard description Language, VHDL, Verilog. • Done by HW designers • By simulation, logical modeling & automatic reasoning • Property checking • Done by HW designers & verification experts 8 © Ghiath AL SAMMANE

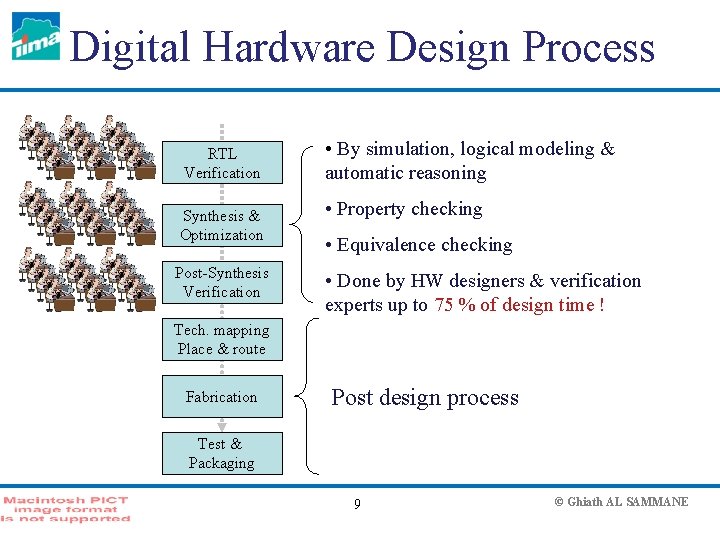
Digital Hardware Design Process RTL Verification Synthesis & Optimization Post-Synthesis Verification • By simulation, logical modeling & automatic reasoning • Property checking • Equivalence checking • Done by HW designers & verification experts up to 75 % of design time ! Tech. mapping Place & route Fabrication Post design process Test & Packaging 9 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 10 © Ghiath AL SAMMANE

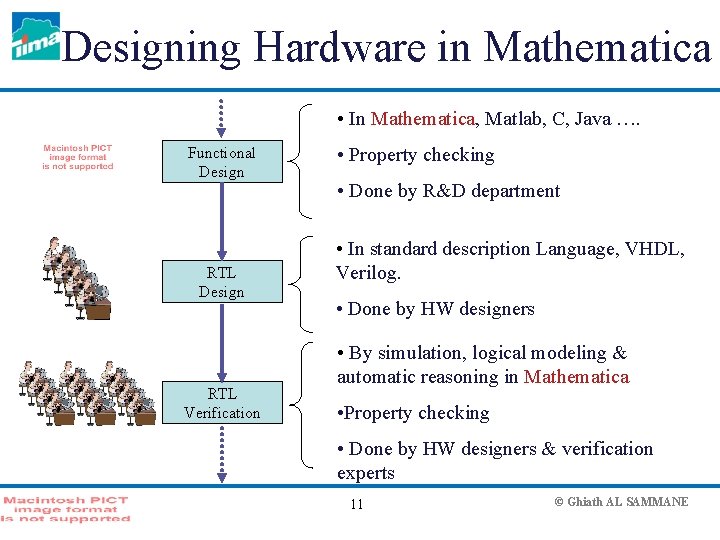
Designing Hardware in Mathematica • In Mathematica, Matlab, C, Java …. Functional Design RTL Verification • Property checking • Done by R&D department • In standard description Language, VHDL, Verilog. • Done by HW designers • By simulation, logical modeling & automatic reasoning in Mathematica • Property checking • Done by HW designers & verification experts 11 © Ghiath AL SAMMANE

Designing HW in Mathematica § Functional Design – Writing the early algorithms, formulas & equations directly in Mathematica – Checking property by numerical & symbolic computation § RTL (register transfer level) design – Writing in standard VHDL – Simulating VHDL in Mathematica numerically & symbolically – Checking properties 12 © Ghiath AL SAMMANE

Designing HW in Mathematica § Functional Design – Writing the early algorithms, formulas & equations directly in Mathematica – Checking property by numerical & symbolic computation § RTL (register transfer level) design – Writing in standard VHDL – Simulating VHDL in Mathematica numerically & symbolically – Checking properties 13 © Ghiath AL SAMMANE

Designing HW in Mathematica § Functional Design – Writing the early algorithms, formulas & equations directly in Mathematica – Checking property by numerical & symbolic computation § RTL (register transfer level) design – Writing in standard VHDL – Simulating VHDL in Mathematica numerically & symbolically – Checking properties 14 © Ghiath AL SAMMANE

Designing HW in Mathematica § Functional Design – Writing the early algorithms, formulas & equations directly in Mathematica – Checking property by numerical & symbolic computation § RTL (register transfer level) design – Writing in standard VHDL – Simulating VHDL in Mathematica numerically & symbolically – Checking properties Finding bugs earlier Less verification effort 15 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 16 © Ghiath AL SAMMANE

First step : VHDL in Mathematica § Modeling the semantic of a VHDL subset – The model must meet the VHDL synthesizable standard – Accept numeric & symbolic inputs – A hierarchical functional model § Simulating the VHDL descriptions – The same results in numeric cases as within standard simulators – Optimized for symbolic simulation § Checking properties about the symbolic results – Pattern matching, sat solving, BDD, theorem proving… 17 © Ghiath AL SAMMANE

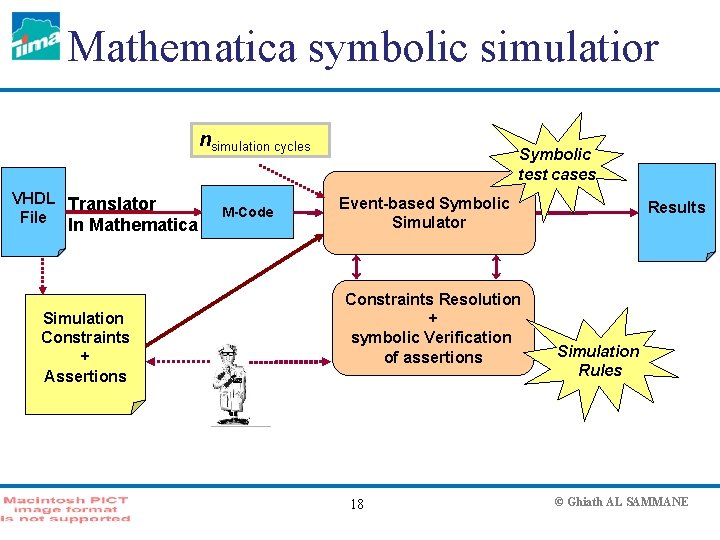
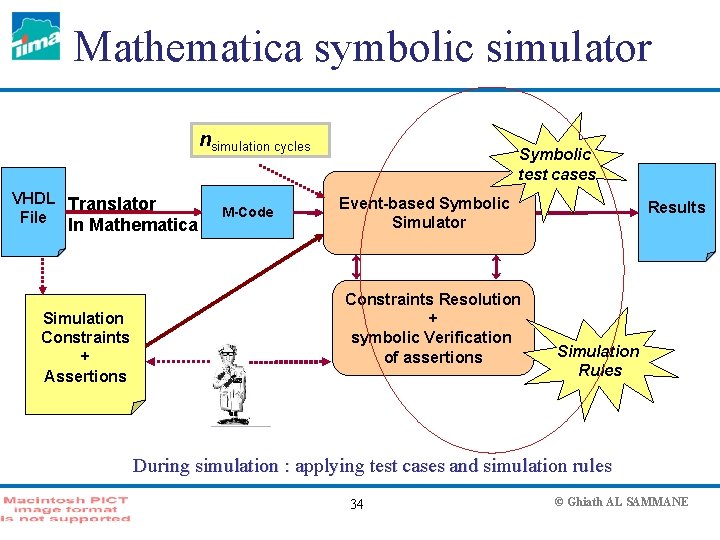
Mathematica symbolic simulatior nsimulation cycles VHDL Translator File In Mathematica Simulation Constraints + Assertions M-Code Symbolic test cases Event-based Symbolic Simulator Constraints Resolution + symbolic Verification of assertions 18 Results Simulation Rules © Ghiath AL SAMMANE

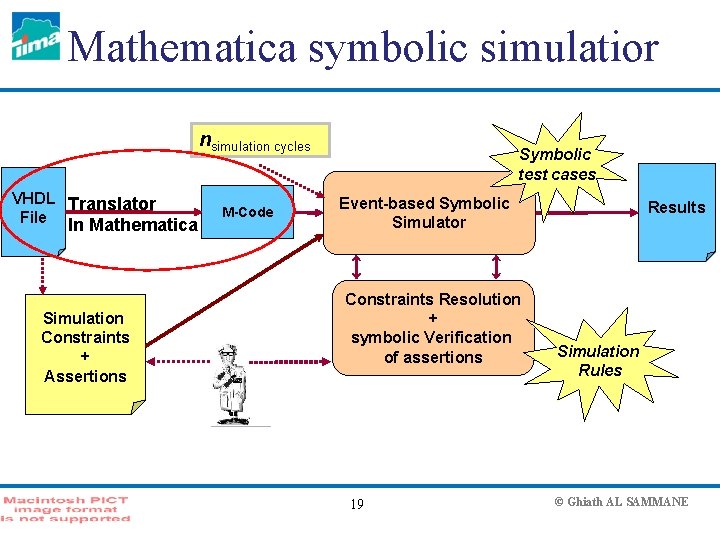
Mathematica symbolic simulatior nsimulation cycles VHDL Translator File In Mathematica Simulation Constraints + Assertions M-Code Symbolic test cases Event-based Symbolic Simulator Constraints Resolution + symbolic Verification of assertions 19 Results Simulation Rules © Ghiath AL SAMMANE

A VHDL example : entity two_arbiter is Clock port ( Clock : in bit; Reset : in bit; Req 1 : in bit; Req 2 : in bit; Ack 1 : out bit; Ack 2 : out bit); end two_arbiter ; Reset Req 1 Req 2 Two requests arbiter Ack 1 Ack 2 Priority is given to the request Req 2 20 © Ghiath AL SAMMANE

A VHDL example : if req 1='1' and req 2='0' then ack 1<='1'; architecture behavior of two_arbiter ack 2<='0'; is elsif req 2='1' then begin -- behavior ack 2<='1'; synchronous: process (clock, reset) ack 1<='0'; begin -- process synchronous else if reset = '0' then ack 1<='0'; ack 2<='0'; end if; elsif clock'event and clock = '1' end if; then -- rising clock edge end process synchronous; end behavior; 21 © Ghiath AL SAMMANE

The M-code § The Mathematica function that models the execution of the VHDL entity-architecture for one clock cycle § M-code (Mathematica COnditional DEscription) § Extracted automatically from the VHDL description § Hierarchy is supported 22 © Ghiath AL SAMMANE

The M-code of the example A VHDL example : The Mathematica equivalent : entity two_arbiter is port ( Clock : in bit; Reset : in bit; Req 1 : in bit; Req 2 : in bit; Ack 1 : out bit; Ack 2 : out bit); Clear[two$arbiter$behavior]; Set. Attributes[two$arbiter$behavior, Hold. All]; two$arbiter$behavior[ack 1_, ack 1$1_, ack 2$1_, clock$0_, req 1_, req 2_, reset$0_]: = end two_arbiter ; 23 © Ghiath AL SAMMANE

The M-code of the example A VHDL example : The Mathematica equivalent : entity two_arbiter is port ( Clock : in bit; Reset : in bit; Req 1 : in bit; Req 2 : in bit; Ack 1 : out bit; Ack 2 : out bit); Clear[two$arbiter$behavior]; Set. Attributes[two$arbiter$behavior, Hold. All]; two$arbiter$behavior[ack 1_, ack 1$1_, ack 2$1_, clock$0_, req 1_, req 2_, reset$0_]: = end two_arbiter ; 24 © Ghiath AL SAMMANE

The M-code of the example A VHDL example : The Mathematica equivalent : entity two_arbiter is port ( Clock : in bit; Reset : in bit; Req 1 : in bit; Req 2 : in bit; Ack 1 : out bit; Ack 2 : out bit); Clear[two$arbiter$behavior]; Set. Attributes[two$arbiter$behavior, Hold. All]; two$arbiter$behavior[ack 1_, ack 1$1_, ack 2$1_, clock$0_, req 1_, req 2_, reset$0_]: = end two_arbiter ; 25 © Ghiath AL SAMMANE

The M-code of the example A VHDL example : The Mathematica equivalent : entity two_arbiter is port ( Clock : in bit; Reset : in bit; Req 1 : in bit; Req 2 : in bit; Ack 1 : out bit; Ack 2 : out bit); Clear[two$arbiter$behavior]; Set. Attributes[two$arbiter$behavior, Hold. All]; two$arbiter$behavior[ack 1_, ack 1$1_, ack 2$1_, clock$0_, req 1_, req 2_, reset$0_]: = end two_arbiter ; 26 © Ghiath AL SAMMANE

Signal modeling § Three values are needed § The current value at time t, (S) § The old value at time (t-1), (S$0) § The next value at time (t+1), (S$1) § Old values are used only for detecting events (Sig(t) Sig (t-1)) 27 © Ghiath AL SAMMANE

The M-code body § Each concurrent statement in the architecture is rewritten as a sequential process § From these processes we extract automatically a list of assignments § One assignment for each object in the design : the transfer function of the object (signal or variable) § Simulates the behavior of the circuit for an abstract time unit called cycle 28 © Ghiath AL SAMMANE

Modeling assignments § The signal assignment function : Next. Sig[ S, F(S 1, S 2, …, Sn)]] § It gives the next value of S knowing the current and the old values of design objects (S 1, S 2, …, Sn) § F is an if-then-else expression (Ife) 29 © Ghiath AL SAMMANE

A VHDL example : if req 1='1' and req 2='0' then ack 1<='1'; architecture behavior of two_arbiter is ack 2<='0'; begin -- behavior elsif req 2='1' then synchronous: process (clock, reset) ack 2<='1'; begin -- process synchronous ack 1<='0'; if reset = '0' then else ack 1<='0'; ack 2<='0'; ack 1<='0'; elsif clock'event and clock = '1' then ack 2<='0'; - rising clock edge end if; end process synchronous; end behavior; 30 © Ghiath AL SAMMANE

The M-code of the architecture § The process is a set of signal assignments : {Next. Sig[ack 1$1, Ife[equal[reset, 0], 0, Ife[and[event[clock], equal[clock, 1]], Ife[and[equal[req 1, 1], equal[req 2, 0]], 1, 0], ack 1] ] ] 31 , Next. Sig[ack 2$1, Ife[equal[reset, 0], 0 , Ife[and[event[clock], equal[clock, 1]], Ife[and[equal[req 1, 1], equal[req 2, 0]], 0, Ife[equal[req 2, 1], 1, 0] ], ack 2]] ] } © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 32 © Ghiath AL SAMMANE

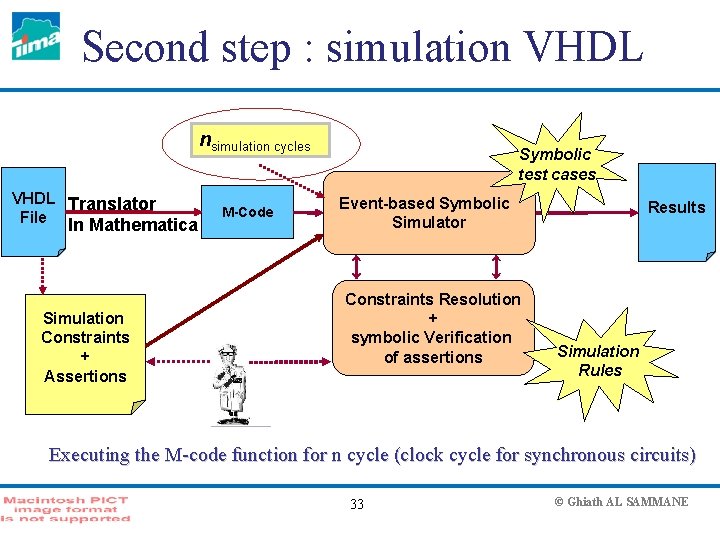
Second step : simulation VHDL nsimulation cycles VHDL Translator File In Mathematica Simulation Constraints + Assertions M-Code Symbolic test cases Event-based Symbolic Simulator Constraints Resolution + symbolic Verification of assertions Results Simulation Rules Executing the M-code function for n cycle (clock cycle for synchronous circuits) 33 © Ghiath AL SAMMANE

Mathematica symbolic simulator nsimulation cycles VHDL Translator File In Mathematica Simulation Constraints + Assertions M-Code Symbolic test cases Event-based Symbolic Simulator Constraints Resolution + symbolic Verification of assertions Results Simulation Rules During simulation : applying test cases and simulation rules 34 © Ghiath AL SAMMANE

Simulation algorithm Initialize(Design. Object) For cycle : = 1 to n do Apply-test-vectors(inputs) Mcode(Design. Object) Verify(Assertion) Update(Design. Object) Print(Selected. Results) End for 35 © Ghiath AL SAMMANE

Simulation Rules § Used during the execution of M-code § Simplification rules – Ife[True, x_, _] x; – Ife[False, _, y_] y; – Ife[_, y_] y; § Normalization rules – Ife[a_, b_, c_], x_, y_] Ife[a, Ife[b, x, y], Ife[c, x, y]]; § Evaluation rules – Ife[cond_, x_, y_] IFE[cond, Assuming[cond, simplify[x]], Assuming[Not[cond], simplify[y]]]; 36 © Ghiath AL SAMMANE

The M-code of the architecture § The process is a set of signal assignments : {Next. Sig[ack 1$1, Ife[equal[reset, 0], 0, Ife[and[event[clock], equal[clock, 1]], Ife[and[equal[req 1, 1], equal[req 2, 0]], 1, 0], ack 1] ] ] 37 , Next. Sig[ack 2$1, Ife[equal[reset, 0], 0 , Ife[and[event[clock], equal[clock, 1]], Ife[and[equal[req 1, 1], equal[req 2, 0]], 0, Ife[equal[req 2, 1], 1, 0] ], ack 2]] ] } © Ghiath AL SAMMANE

Simulation of the example § Most inputs are symbols, one simulation test case is equivalent to a lot of numeric ones § The symbolic expression of Ack 1 – IFE[RESET == 0, 0, IFE[REQ 1 == 1 && REQ 2 == 0, 1, 0]] § The symbolic expression of Ack 2 – IFE[RESET == 0, 0, IFE[REQ 1 == 1 && REQ 2 == 0, 0, IFE[REQ 2 == 1, 1, 0]]] 38 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 39 © Ghiath AL SAMMANE

Checking properties § What can we do with huge If-then-else expressions? – The designer writes a property that the circuit should satisfy – After the simulation, the symbolic expression of the assertion should be evaluated to true or false § Property are checked by – Using comparison to direct specifications written in Mathematica – Using a Boolean prover in Mathematica – Using an external theorem prover 40 © Ghiath AL SAMMANE

Boolean prover in Mathematica § A prototype is under test § Take a normalized if-then-else and gives a counter example if theorem is wrong and prove it otherwise § Built by the association of : – an implementation of the shared-BDD rewriting in Mathematica – Make use of the Find. Instance function in Mathematica 41 © Ghiath AL SAMMANE

Checking properties of the example § mutex : assert not (Ack 1 and Ack 2) § serve : assert Req 1 or Req 2 Ack 1 or Ack 2 § waste : assert Ack 1 req 1 § waste : assert Ack 2 req 2 § All these properties are proved by by our Boolean prover in Mathematica and by ACL 2 42 © Ghiath AL SAMMANE

Sat. Bit : checking the arbiter Sat. Bit : Gives an example that the expression is satisfaisable, False other wise. In[24]: = Sat. Bit[ack 2] Sat, example: Out[24]= {{REQ 1 -> 1, REQ 2 -> 1, RESET -> 1}} In[25]: = Sat. Bit[ack 1&&ack 2] Out[25]= False 43 © Ghiath AL SAMMANE

Proving properties by ACL 2 § An inductive theorem prover § An automatic link with Mathematica § The main function is Implies. Acl 2[p, q] – Prove by Acl 2 that p q Example: – Implies. Acl 2[ And[ bitp[REQ 1, REQ 2, RESET], RESET == 1 , ack 1 == 1 ], REQ 1 == 1] True 44 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 45 © Ghiath AL SAMMANE

Successful applications § Validation on research and academic cases § Symbolic simulation and a verification of a network on chip (a university circuit) § Symbolic simulation of an industrial cryptographic component implementation § Symbolic simulation and property verification of a DRAM specification that comes from STMicroelectronics 46 © Ghiath AL SAMMANE

Outline § § § § What is TIMA? Digital hardware design process Modeling Hardware in Mathematica VHDL simulation in Mathematica Verification & symbolic simulation Property checking Successful applications Conclusion 47 © Ghiath AL SAMMANE

Conclusion : achievements § A VHDL to Mathematica compiler is built § A hardware simulator in Mathematica is implemented § We prove properties about results – A Boolean prover is implemented in Mathematica (automatic) – A link to an external theorem prover is achieved (expert in proof may be needed when proof fails) § Application on various industrial circuits 48 © Ghiath AL SAMMANE

Conclusion : What is next ? § Writing a user manual § Building an interface § Supporting Property Specification Language (PSL) § A Demo at DATE 2005 (Design Automation & Test in Europe) 49 © Ghiath AL SAMMANE

Thank you 50 © Ghiath AL SAMMANE

If-then-else expression (Ife) Ife_expr : : = Symbol | Number | True | False | Boolean_Expression | Arithmetic_Expression | Ife[Ife_expr, Ife_expr] 51 © Ghiath AL SAMMANE