Using Mat Lab and Excel to Solve Building

Using Mat. Lab and Excel to Solve Building Energy Simulation Problems Jordan Clark jdclark@utexas. edu

Objectives • Intro to Mat. Lab (if needed) • Briefly discuss linear equations • Solving systems of non-linear equations – Using solve function • Example 1 – Using loops to solve for multiple time steps • Example 2 – Importing data from Excel • Example 3

Linear Equations in MATLAB • Solve system of equations: 3 x +2 y –z = 10 -x +3 y +2 z = 5 x -y -z = -1

Linear Equations in MATLAB •

Linear Equations in MATLAB • 3 ways to solve in MATLAB: – Inv – A^-1 – Left division

Linear Equations in MATLAB • For all three, first define matrices: A= [3 2 -1; -1 3 2; 1 -1 -1]; B= [10; 5; -1]; • Can be solved by any of the following syntaxes: X=inv(A)*B X=A^-1*B X=AB NOT X=A/B or X=BA • Each gives equivalent answer • Left division is more computationally efficient: less time to compute for large matrices

Non-Linear Equations in MATLAB • Distinguish between symbolic variables (ones you will solve for) and variables with numeric values (i. e. e, F 12, etc. ) • Define symbolic variables: – Can create multiple symbolic variables at once with syms command – Syntax: syms x y z a b c or syms T 1 T 2 T 3

Non-Linear Equations in MATLAB • Say we have defined symbolic variable x and want to solve an equation for x. • With symbolic variables defined, create equation using syntax: E 1=x-3 • Notice your equation must be in the form f(x)=0 • If it is not, rearrange it so it is

Non-Linear Equations in MATLAB • We can now use solve function to find x: • If we just write solve (E 1) we will get ans = 3 • If we want to redefine x as the solution, we can input x= solve(E 1)

Non-Linear Equations in MATLAB • For systems of equations, process is similar. – Define variables using syms – Write multiple homogeneous equations e. g. E 1= x + y + z +2 E 2= 3*x -2*y + z E 3= -x + y -4*z +6 – Then use [x, y, z]=solve(E 1, E 2, E 3) – Variables must be listed in alphabetical order on left side because right side outputs answers in alphabetical order of symbolic variables

Non-Linear Equations in MATLAB • Sometimes you will be working with both symbolic and numerical variables. • This is ok.

Non-Linear Equations in MATLAB Example 1: Find both T 2 and Q for the steady state conduction problem, given k=4 W/m. K, wall thickness is 0. 2 m, T 1=30, T 3=40, and the area of the wall is 4 m 2 Q T 1 T 2 T 3

Non-Linear Equations in MATLAB Example 1 Code: k=4; %W/m. K A=4; %m^2 L=0. 1; %m T 1=30; %degrees C T 3=40; syms Q T 2; E 1= k*A/L*(T 3 -T 2)-Q; E 2= k*A/L*(T 2 -T 1)-Q; [Q, T 2]=solve(E 1, E 2) Output: Q= 800 T 2 = 35

Non-Linear Equations in MATLAB Example 2: Using a loop to solve for multiple time steps • Now suppose the temperature of the outside wall changes every hour, in discrete jumps (steady state assumption can be used for each hour) • We need an efficient means of calculating T 2 and Q for each hour • Will use a loop

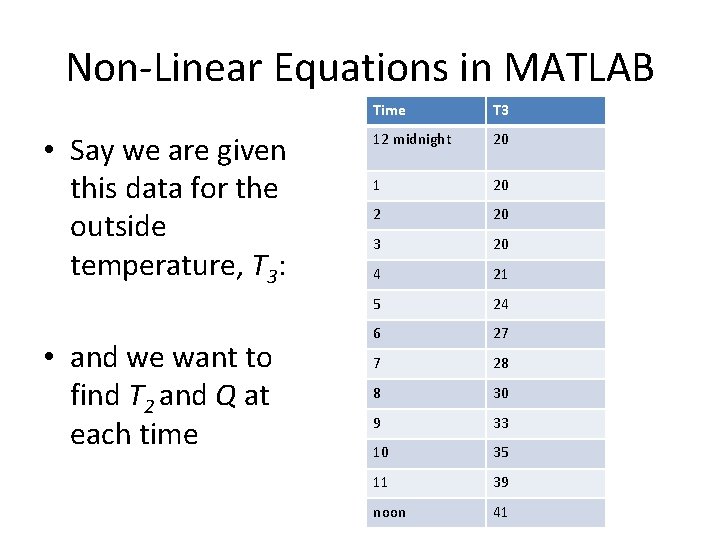
Non-Linear Equations in MATLAB • Say we are given this data for the outside temperature, T 3: • and we want to find T 2 and Q at each time T 3 12 midnight 20 1 20 2 20 3 20 4 21 5 24 6 27 7 28 8 30 9 33 10 35 11 39 noon 41

Non-Linear Equations in MATLAB Example 2 • 1 st create an array with the temperatures: T 3=[20 20 21 24 27 28 30 33 35 39 41] • Then loop through each value of T 3 to calculate a corresponding value of Q and T 2, and store these values in a Q and T 2 array

Non-Linear Equations in MATLAB Example 2 code: k=4; %W/m. K A=4; %m^2 L=0. 1; %m T 1=30; %degrees C T 3=[20 20 21 24 27 28 30 33 35 39 41]; syms Q T 2; for i=1: 13 E 1= k*A/L*(T 3(i)-T 2)-Q; E 2= k*A/L*(T 2 -T 1)-Q; [Qarray(i), T 2 array(i)]=solve(E 1, E 2) %input temperature array % define symbolic variables % tells the program to loop through 13 iterations % (corresponding to 13 hours for which we have data) %notice an individual value of the data is called for T 3 %by using the index "i" in T 3(i) %we save our data in a separate array, % which is appended automatically each iteration end T 2 array=double(T 2 array) %when doing symbolic math, answer is often returned in fractional form. %to convert it to decimal form, use the function "double", as in double precision

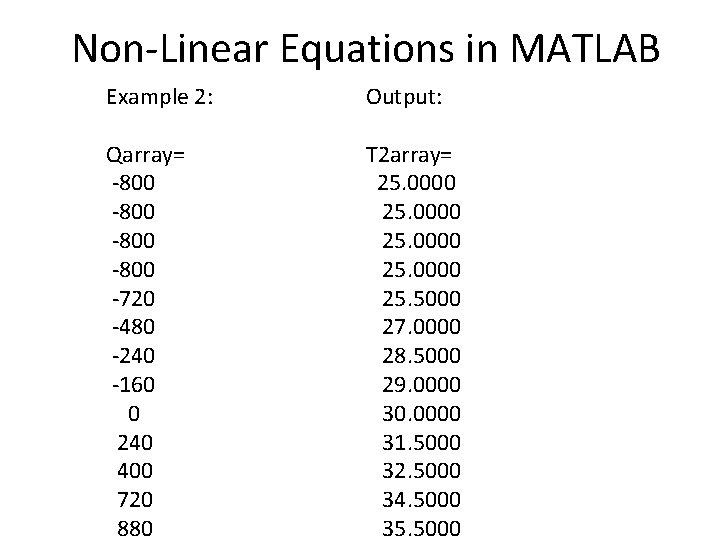
Non-Linear Equations in MATLAB Example 2: Output: Qarray= -800 -720 -480 -240 -160 0 240 400 720 880 T 2 array= 25. 0000 25. 5000 27. 0000 28. 5000 29. 0000 30. 0000 31. 5000 32. 5000 34. 5000 35. 5000

Non-Linear Equations in MATLAB Example 3: Importing Data from Excel • Sometimes we have a lot of data and cannot input it by hand, e. g. TMY data • There a few ways to import data from Excel – Cut and paste – Use import wizard by selecting File > Import Data or Use function uiimport • When using the wizard, make sure the file is saved in your working directory

Non-Linear Equations in MATLAB Example 3 • Say we now are not given T 3, but we have an outdoor convection coefficient, h, which changes with time, and an outdoor air temperature. Q T 1=30 T 2 T 3 Tout • We want to find all T values and Q using the import wizard

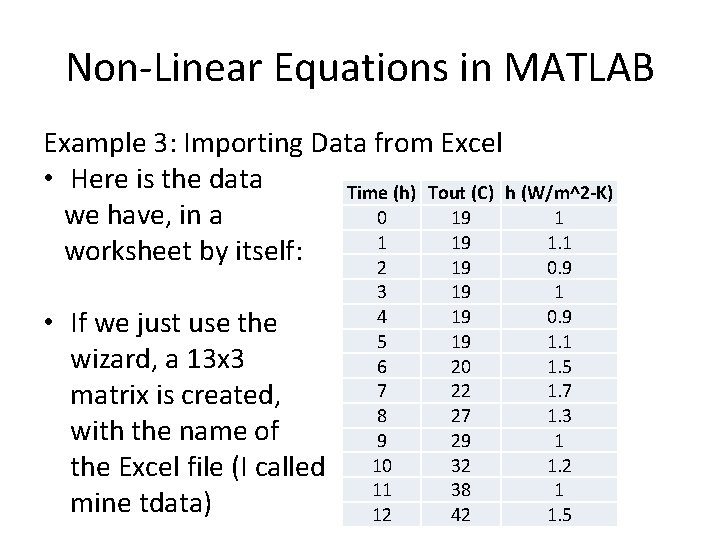
Non-Linear Equations in MATLAB Example 3: Importing Data from Excel • Here is the data Time (h) Tout (C) h (W/m^2 -K) we have, in a 0 19 1 1 19 1. 1 worksheet by itself: 2 19 0. 9 • If we just use the wizard, a 13 x 3 matrix is created, with the name of the Excel file (I called mine tdata) 3 4 5 6 7 8 9 10 11 12 19 19 19 20 22 27 29 32 38 42 1 0. 9 1. 1 1. 5 1. 7 1. 3 1 1. 2 1 1. 5

Non-Linear Equations in MATLAB Example 3: Importing Data from Excel We can make separate arrays if we like for each variable by using commands such as >> Tout=tdata (: , 2) Tout =19 19 19 20 22 27 29 32 38 42 %which says the array “Tout” is the 2 nd column of “tdata”

Non-Linear Equations in MATLAB Example 3: Importing Data from Excel • Once we identify the h values in a similar way, we can solve our problem • Code on next slide

Non-Linear Equations in MATLAB Example 3 Code k=4; %W/m. K A=4; %m^2 L=0. 1; %m T 1=30; %degrees C syms Q T 2 T 3; for i=1: 13 E 1= k*A/L*(T 3 -T 2)-Q; E 2= k*A/L*(T 2 -T 1)-Q; E 3= h(i)*A*(Tout(i)-T 3)-Q; %we now have 3 eqns + 3 unknowns %notice indices on h and Tout [Qarray(i), T 2 array(i), T 3 array(i)]=solve(E 1, E 2, E 3) end Qarray=double(Qarray)' T 2 array=double(T 2 array)' T 3 array=double(T 3 array)'

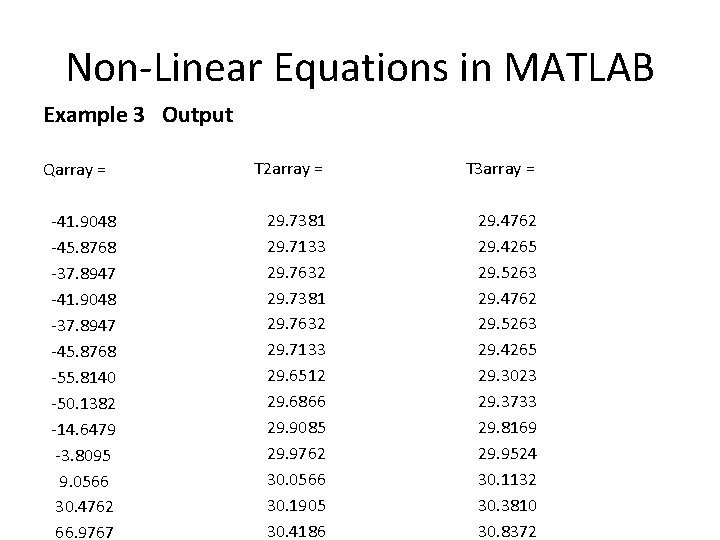
Non-Linear Equations in MATLAB Example 3 Output Qarray = -41. 9048 -45. 8768 -37. 8947 -41. 9048 -37. 8947 -45. 8768 -55. 8140 -50. 1382 -14. 6479 -3. 8095 9. 0566 30. 4762 66. 9767 T 2 array = T 3 array = 29. 7381 29. 7133 29. 7632 29. 7381 29. 7632 29. 7133 29. 6512 29. 6866 29. 9085 29. 9762 30. 0566 30. 1905 30. 4186 29. 4762 29. 4265 29. 5263 29. 4762 29. 5263 29. 4265 29. 3023 29. 3733 29. 8169 29. 9524 30. 1132 30. 3810 30. 8372

Conclusion • Should be everything you need to finish homework • Additional help (2 equation model form the class) on the course website, handouts section • Please contact me with questions about Matlab or about B. E. S. jdclark@utexas. edu • Questions now? ?