Using Manifold Structure for Partially Labeled Classification by

Using Manifold Structure for Partially Labeled Classification by Belkin and Niyogi, NIPS 2002 Presented by Chunping Wang Machine Learning Group, Duke University November 16, 2007

Outline • • • Motivations Algorithm Description Theoretical Interpretation Experimental Results Comments

Motivations (1) Why manifold structure is useful? Ø Data lies on a lower-dimensional manifold – a dimension reduction is preferable an example: a handwritten digit 0 Usually, dimensionality is the number of pixels, typically very high (256)

Motivations (1) Why manifold structure is useful? Ø Data lies on a lower-dimensional manifold – a dimension reduction is preferable an example: a handwritten digit 0 f 1 * f 2 * d 1 d 2 Ideally, 5 -dimensional features Usually, dimensionality is the number of pixels, typically very high (256)

Motivations (1) Why manifold structure is useful? Ø Data lies on a lower-dimensional manifold – a dimension reduction is preferable an example: a handwritten digit 0 f 1 * f 2 * d 1 d 2 Ideally, 5 -dimensional features Actually, Usually, a higher dimensionality, but perhaps no more than several dozens dimensionality is the number of pixels, typically far higher (256)

Motivations (2) Why manifold structure is useful? Ø Data representation in the original space is unsatisfactory labeled unlabeled In the original space 2 -d representation with Laplacian Eigenmaps

Algorithm Description (1) Semi-supervised classification k points First s are labeled (s<k) • for binary cases Constructing the Adjacency Graph if i is among n nearest neighbors of j or j is among n nearest neighbors of i • Eigenfunctions compute , corresponding to the p smallest eigenvelues for the graph Laplacian L = D-W,

Algorithm Description (2) Semi-supervised classification k points First s are labeled (s<k) • Building the classifier minimize the error function space of coefficients a the solution is • for binary cases Classifying unlabeled points (i >s) over the

Theoretical Interpretation (1) For a manifold , the eigenfunctions of its Laplacian form a basis for the Hilbert space , i. e. , any function with can be written as eigenfunctions satisfying The simplest nontrivial example: the manifold is a unit circle S 1 Fourier series

Theoretical Interpretation (2) Smoothness measure S: a small S means “smooth” For unit circle S 1 Generally Smaller eigenvalues correspond to smoother eigenfunctions (lower frequency) is a constant function In terms of the smoothest p eigenfunctions, the approximation of an arbitrary function

Theoretical Interpretation (3) Back to our problem with finite number of points The solution of a discrete version For binary classification, the alphabet of the function f only contains two possible values. For M-ary cases, the only difference is the number of possible values is more than two.

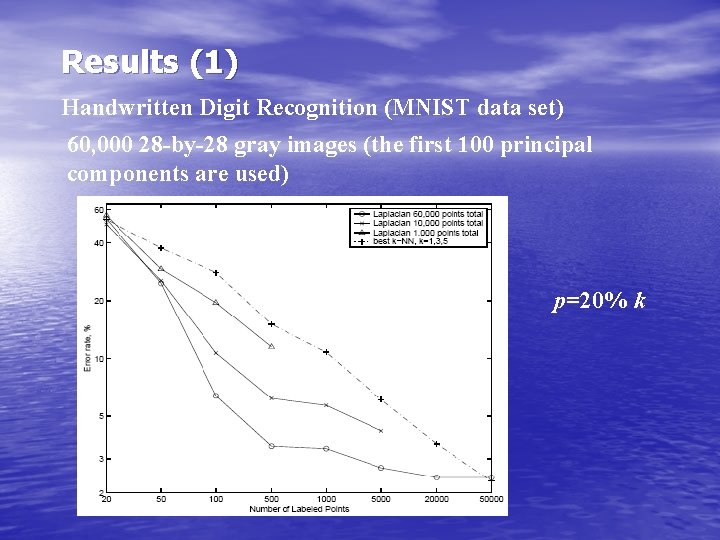
Results (1) Handwritten Digit Recognition (MNIST data set) 60, 000 28 -by-28 gray images (the first 100 principal components are used) p=20% k

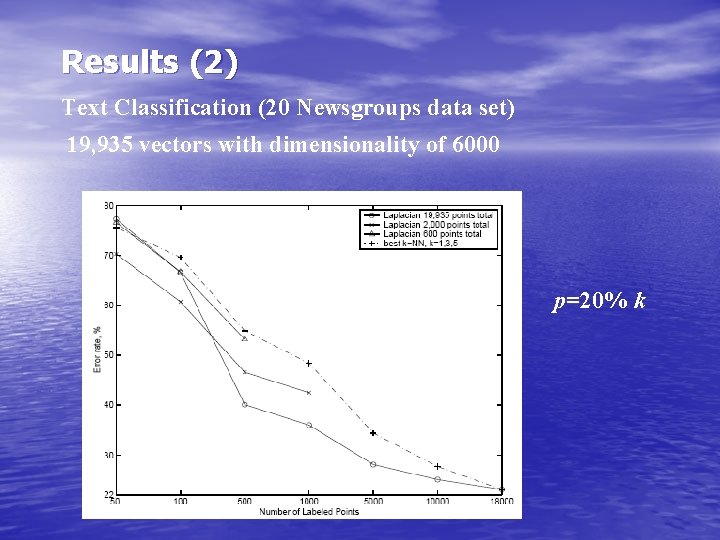
Results (2) Text Classification (20 Newsgroups data set) 19, 935 vectors with dimensionality of 6000 p=20% k

Comments § This semi-supervised algorithm essentially converts the original problem to a linear regression problem in a new space with lower dimensionality. § The approach to solve this linear regression problem is the standard least square estimation. § Only n nearest neighbors are considered for each data point, thus the computation for eigen-decomposition is reduced. § Little additional computation is expended after dimensionality reduction. More comments ……