Using LISP as tool for mathematical experimentation Hugo

Using LISP as tool for mathematical experimentation Hugo Alex Diniz – UFOPA – Brasil ICME 13 – Hamburg

First puzzle – Cherryl’s Birthday � Problem 24 of 2015 Singapore and Asian Schools Math Olympiad (SASMO). Aimed to 14 -year-old students. � It was internet viral in 2015. � This type of puzzle is known as “Freudenthal Problem”. � In 1969, Hans Freudenthal (1905 -1990) proposed a problem like this. �

First puzzle – Cherryl’s Birthday Albert and Bernard just met Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates: May 15, 16, 19 – June 17, 18 – July 14, 16 – August 14, 15, 17 Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively. Albert: I don't know when Cheryl's birthday is, but I know that Bernard doesn't know, either. Bernard: At first I didn’t know when Cheryl's birthday is, but I know now. Albert: Then I also know when Cheryl's birthday is. So when is Cheryl's birthday?

Other version of the dialog Albert: My month has more than one associated date. But all associated dates has more than one associated month. So Bernard doesn’t know the month. (Then the month is July or August!!!) May June July August 15 14 14 16 17 16 15 17 19 18

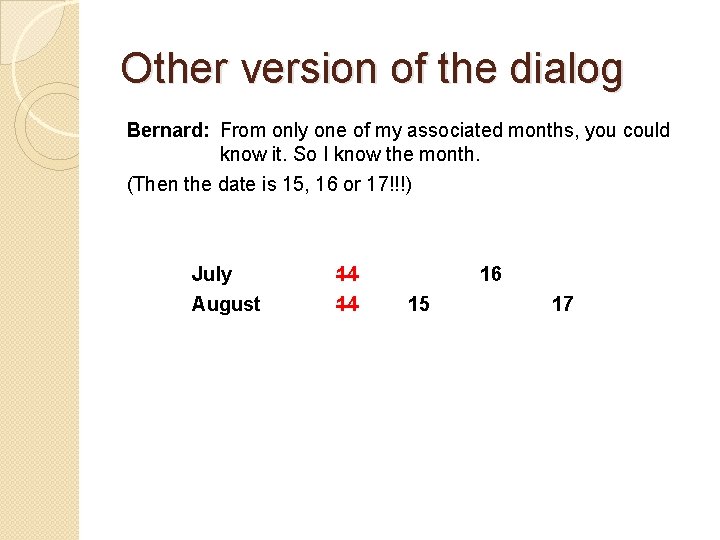
Other version of the dialog Bernard: From only one of my associated months, you could know it. So I know the month. (Then the date is 15, 16 or 17!!!) July August 14 14 16 15 17

Other version of the dialog Albert: From only one of my associated dates, you could know it. So I know the date. (The birthday is July 16!!) July August 14 14 16 15 17

Second Puzzle – Three Daughters A man in my neighborhood has three daughters. One day when I asked their ages he said, “The product of their ages is 36. ” When I still couldn’t find their ages he said, “Ok. I’ll give you another clue: the sum of their ages is same as the number of my house. ” I knew the number but still couldn’t calculate their ages. So the man gave me a last clue, “My eldest daughter lives upstairs. ” Finally I was able to figure out their ages. How old are they?

Solution – First Function (defun divisors-pair (n) (loop for i from 1 to (isqrt n) when (zerop (mod n i)) collect (list i (/ n i)) ) ) (divisors-pair 36) > ((1 36) (2 18) (3 12) (4 9) (6 6))

Solution – Second Function (defun divisors-triple (n) (loop for x in (divisors-pair n) append (loop for y in (divisors-pair (second x)) collect (sort (list (first x) (first y) (second y)) #'<=)) into l finally (return (remove-duplicates l : test #'equal : fromend T) ) (divisors-triple 36) > ((1 1 36) (1 2 18) (1 3 12) (1 4 9) (1 6 6) (2 2 9) (2 3 6) (3 3 4))

Solution – Third Function (defun sum-duplicated (l) (loop for x in l when (< 1 (count (reduce #'+ x) l : key #'(lambda (l) (reduce #'+ l)))) collect x ) ) (sum-duplicated (divisors-triple 36)) > ((1 6 6) (2 2 9))

LISP Examples (+ -2 3 5) >6 (* 6 8 3) > 144 (* 3 (+ 1 3) (- 5 3)) > 24 (gcd 12 18) >6 (lcm 12 18) > 36

LISP Examples (loop for n from 1 to 10 when (evenp n) collect n) > (2 4 6 8 10) (loop for n from 1 to 20 when (zerop (mod n 4)) collect n) > (4 8 12 16 20)

Third Puzzle – Impossible Problem Proposed by Martin Gardner (1914 – 2010) � Published in his column Mathematical Games at Scientific American magazine in 1979 � The problem is that this problem is really impossible!!! � He modified the original Freudenthal Problem �

Third Puzzle – Impossible Problem Two numbers (not necessarily different) are chosen from the range of positive integers greater than 1 and not greater than 20. Only the sum of the two numbers is given to mathematician S. Only the product of the two is given to mathematician P. On the telephone S says to P: “I see no way you can determine my sum. ” An hour later P calls him to say: “I know your sum. ” Later S calls P again to report: “Now I know your product. ” What are the two numbers?

Other version of the dialog S: I verified all my associated products. None is a revealing product. You don’t know my sum. (Then the sum is 11!!!) (loop for sum from 4 to 40 when (notany #'revealing (products sum)) collect sum ) > (11)

Other version of the dialog P: Only one of associated sum has this property. Now I know your sum. (This is not more information than we already have) S: I checked my associated product and only one would allow you to know my sum. (Impossible. All his associated products allow the conclusion) (products 11) > (18 24 28 30)

Forth Puzzle – Freudenthal Problem Published in German in 1969 � Translated by David Sprows and published in 1976 � � The problem has solution!!!

Forth Puzzle – Freudenthal Problem Let x and y be two numbers with 1<x<y and x+y≤ 100. Suppose S is given the value x+y and P is given the value xy. P says: “I don’t know the values of x and y. ” S replies: “I knew that you didn’t know the values. ” P responds: “Oh, then I do know the values of x and y. ” S exclaims: “Oh, then so do I. ” What are the values of x and y?

Other version of the dialog S: I verified all my associated products. None is a revealing product. You don’t know my sum. (defun possible_sums () (loop for sum from 5 to 100 when (notany #'revealing (products sum)) collect sum ) ) (possible_sums) > (11 17 23 27 29 35 37 41 47 53)

Other version of the dialog P: Only one of associated sum has this property. Now I know your sum. (defun possible_products () (loop with list_sums = (possible_sums) for sums in list_sums append (loop for product in (product sum) when (= 1 (length (intersection (sums product) list_sums))) collect product) ) )

Other version of the dialog (possible_products) > (18 24 28 52 76 112 130 50 92 110 140 152 162 170 176 182 54 100 138 154 168 190 198 204 208 96 124 174 216 234 250 276 294 306 160 186 232 252 270 336 340 114 148 238 288 310 348 364 378 390 408 414 418 172 246 280 370 442 480 496 510 522 532 540 552 240 282 360 430 492 520 570 592 612 630 646 660 672 682 690 696 700 702)

Other version of the dialog S: I checked my associated product and only one would allow you to know my sum. (defun solutions () (loop with list_sums = (possible_sums) with list_products = (possible_products) for sum in list_sums for l = (intersection (products sum) list_products) when (= 1 (length l)) collect (push sum l) )) > ((17 52))

Other examples with LISP �Factorial �Fibonacci’s sequence �Prime factorization �Sieve of Eratosthenes