Using Inductive Reasoning to Make Conjectures Geometry Farris

Using Inductive Reasoning to Make Conjectures Geometry Farris 2015

• I can use inductive reasoning to identify patterns and make conjectures. • I can find counterexamples to disprove conjectures.

Identify a Pattern • Monday, Wednesday, Friday, …. • 3, 6, 9, 12, 15, ….

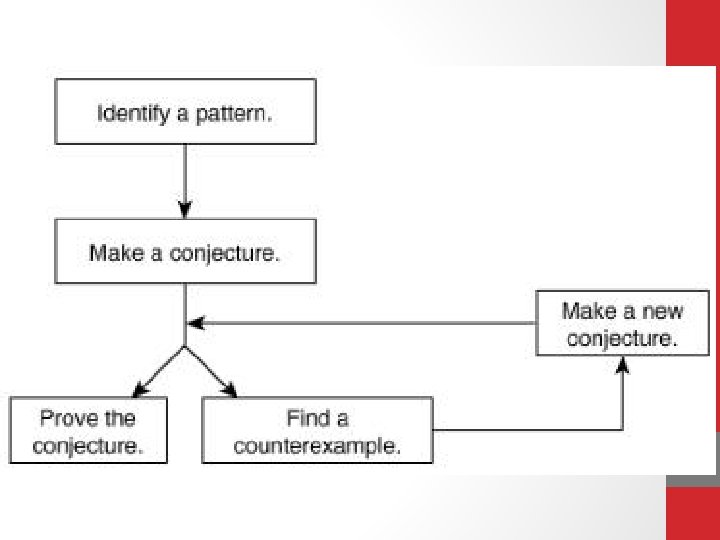
Definitions • Inductive Reasoning: The process of reasoning that a rule or statement is true because specific causes are true. • Conjecture: A statement you believe to be true based on inductive reasoning.

Make a Conjecture • The product of an even number and an odd number is _____. List some examples and look for a pattern. (2)(3) = 6 (2)(5) = 10 (4)(3) = 12 The product of an even number and an odd number is even.

Additional Conjectures • The sum of two positive numbers is _______. • The number of lines formed by 4 points, no three of which are collinear, is ____. positive 6

Counterexample • To show that a conjecture is ALWAYS true, you must prove it. • To prove that a conjecture is false, you have to find only one example in which the conjecture is NOT true. • A counterexample can be a drawing, a statement, or a number.

Finding a Counterexample • For any real number x, x 2 ≥ x. X = 1/2 • Supplementary angels are adjacent.

Word problem • The pattern 1, 1, 2, 3, 5, 8, 13, 21… is Known as the Fibonacci Sequence. Find the next tree terms in the sequence and write a conjecture for the pattern. 34, 55, 89; each term is the sum of the 2 previous terms.

Multiple Choice • Which of the following conjectures is false? • If x is odd then x + 1 is even. • The sum of two odd numbers is even. • The difference of two even numbers is positive. • If x is positive, then –x is negative. The difference of two even numbers is positive.

Multiple Choice • A student conjectures that if x is a prime number, then x + 1 is not prime. Which of the following is a counterexample? • X = 11 • X=6 • X=3 • X=2