Using Graphs in Unstructured and Semistructured Data Mining

Using Graphs in Unstructured and Semistructured Data Mining Soumen Chakrabarti IIT Bombay www. cse. iitb. ac. in/~soumen ACFOCS 2004 Chakrabarti 1

Acknowledgments § § § C. Faloutsos, CMU W. Cohen, CMU IBM Almaden (many colleagues) IIT Bombay (many students) S. Sarawagi, IIT Bombay S. Sudarshan, IIT Bombay ACFOCS 2004 Chakrabarti 2

Graphs are everywhere § § § Phone network, Internet, Web Databases, XML, email, blogs Web of trust (epinion) Text and language artifacts (Word. Net) Commodity distribution networks Internet Map [lumeta. com] ACFOCS 2004 Food Web [Martinez 1991] Chakrabarti Protein Interactions [genomebiology. com] 3

Why analyze graphs? § What properties do real-life graphs have? § How important is a node? What is importance? § Who is the best customer to target in a social network? § Who spread a raging rumor? § How similar are two nodes? § How do nodes influence each other? § Can I predict some property of a node based on its neighborhood? ACFOCS 2004 Chakrabarti 4

Outline, some more detail § Part 1 (Modeling graphs) § What do real-life graphs look like? § What laws govern their formation, evolution and properties? § What structural analyses are useful? § Part 2 (Analyzing graphs) § § ACFOCS 2004 Modeling data analysis problems using graphs Proposing parametric models Estimating parameters Applications from Web search and text mining Chakrabarti 5

Modeling and generating realistic graphs ACFOCS 2004 Chakrabarti 6

Questions § What do real graphs look like? § Edges, communities, clustering effects § What properties of nodes, edges are important to model? § Degree, paths, cycles, … § What local and global properties are important to measure? § How to artificially generate realistic graphs? ACFOCS 2004 Chakrabarti 7

Modeling: why care? § Algorithm design § Can skewed degree distribution make our algorithm faster? § Extrapolation § How well will Pagerank work on the Web 10 years from now? § Sampling § Make sure scaled-down algorithm shows same performance/behavior on large-scale data § Deviation detection § Is this page trying to spam the search engine? ACFOCS 2004 Chakrabarti 8

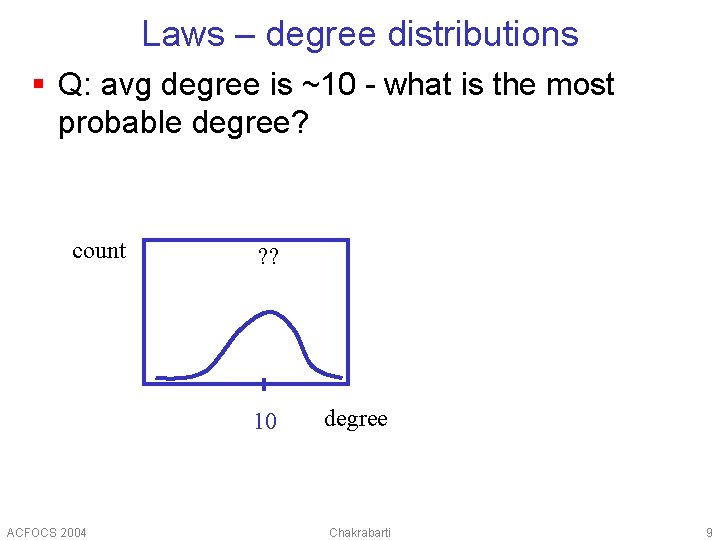
Laws – degree distributions § Q: avg degree is ~10 - what is the most probable degree? count ? ? 10 ACFOCS 2004 degree Chakrabarti 9

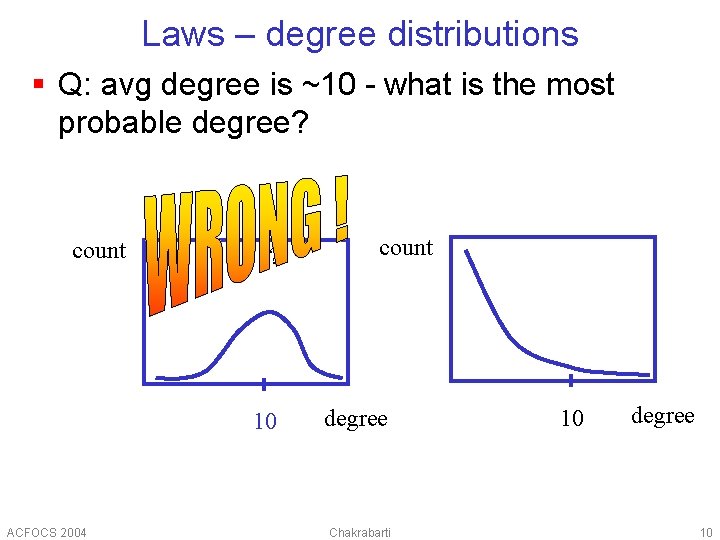
Laws – degree distributions § Q: avg degree is ~10 - what is the most probable degree? count ? ? 10 ACFOCS 2004 count degree Chakrabarti 10 degree 10

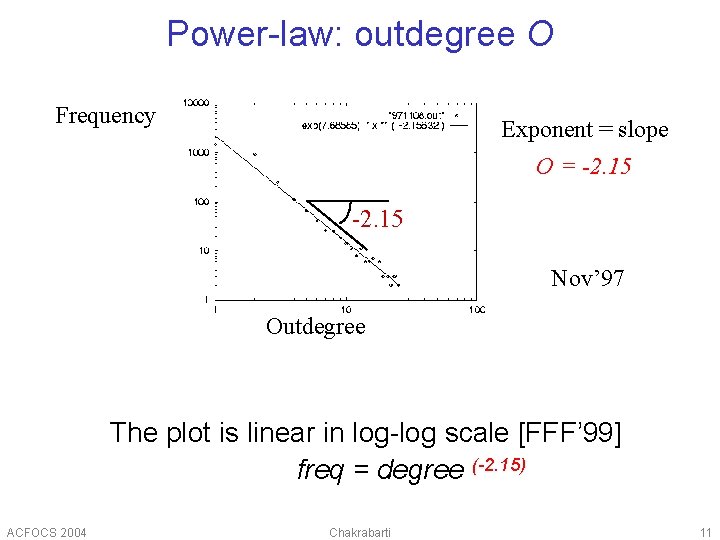
Power-law: outdegree O Frequency Exponent = slope O = -2. 15 Nov’ 97 Outdegree The plot is linear in log-log scale [FFF’ 99] freq = degree (-2. 15) ACFOCS 2004 Chakrabarti 11

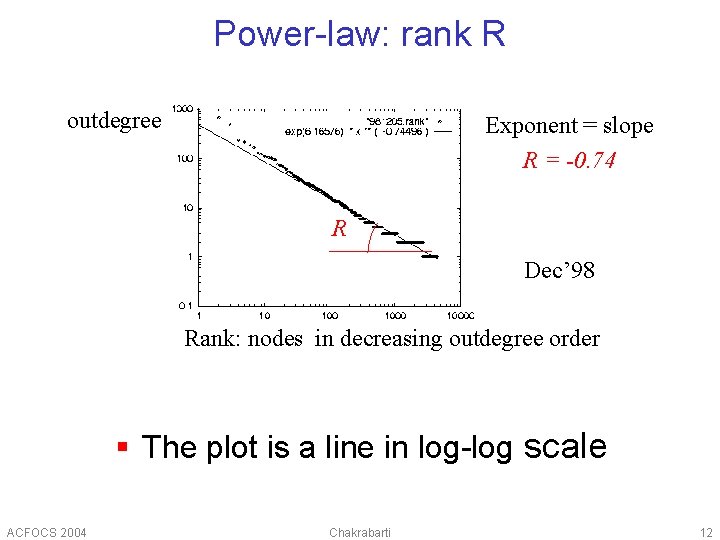
Power-law: rank R outdegree Exponent = slope R = -0. 74 R Dec’ 98 Rank: nodes in decreasing outdegree order § The plot is a line in log-log scale ACFOCS 2004 Chakrabarti 12

Eigenvalues § Let A be the adjacency matrix of graph § The eigenvalue satisfies § A v = v, where v is some vector § Eigenvalues are strongly related to graph topology A B C D ACFOCS 2004 Chakrabarti 13

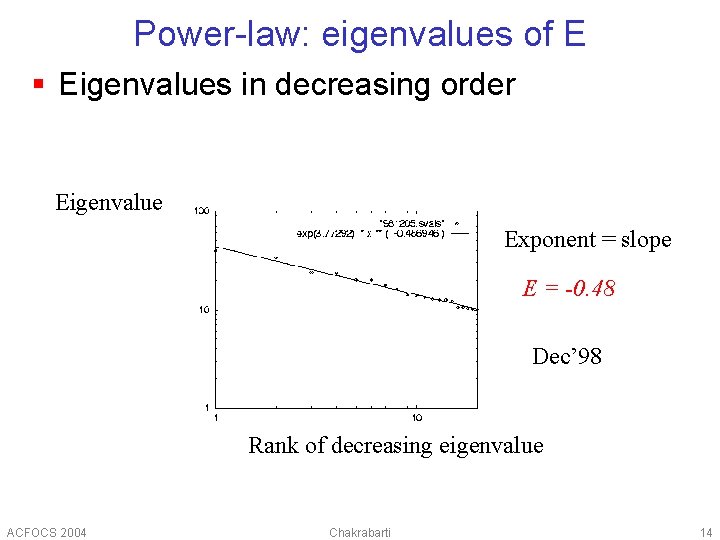
Power-law: eigenvalues of E § Eigenvalues in decreasing order Eigenvalue Exponent = slope E = -0. 48 Dec’ 98 Rank of decreasing eigenvalue ACFOCS 2004 Chakrabarti 14

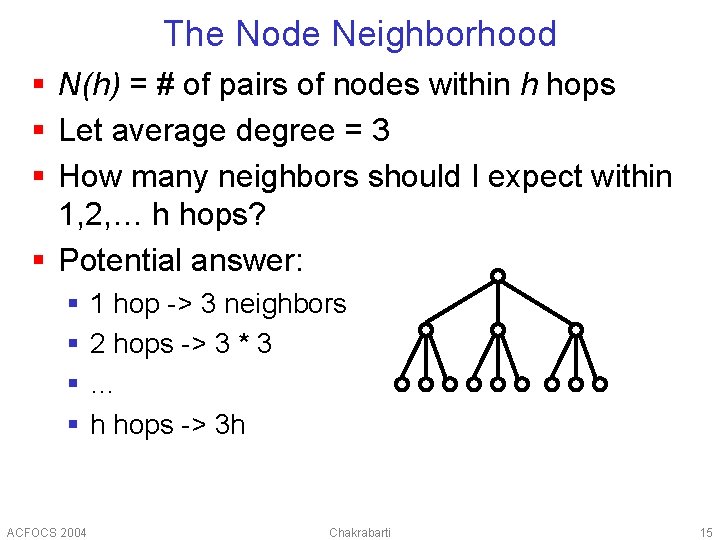
The Node Neighborhood § N(h) = # of pairs of nodes within h hops § Let average degree = 3 § How many neighbors should I expect within 1, 2, … h hops? § Potential answer: § § ACFOCS 2004 1 hop -> 3 neighbors 2 hops -> 3 * 3 … h hops -> 3 h Chakrabarti 15

The Node Neighborhood § N(h) = # of pairs of nodes within h hops § Let average degree = 3 § How many neighbors should I expect within 1, 2, … h hops? § Potential answer: § § ACFOCS 2004 1 hop -> 3 neighbors 2 hops -> 3 * 3 … h hops -> 3 h WE HAVE DUPLICATES! Chakrabarti 16

The Node Neighborhood § N(h) = # of pairs of nodes within h hops § Let average degree = 3 § How many neighbors should I expect within 1, 2, … h hops? § Potential answer: § § ACFOCS 2004 1 hop -> 3 neighbors 2 hops -> 3 * 3 … h hops -> 3 h ‘avg’ degree: meaningless! Chakrabarti 17

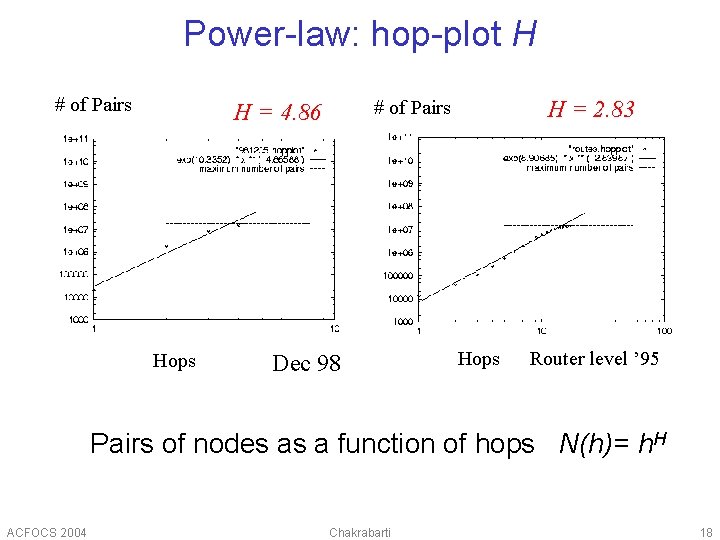
Power-law: hop-plot H # of Pairs Hops H = 2. 83 # of Pairs H = 4. 86 Dec 98 Hops Router level ’ 95 Pairs of nodes as a function of hops N(h)= h. H ACFOCS 2004 Chakrabarti 18

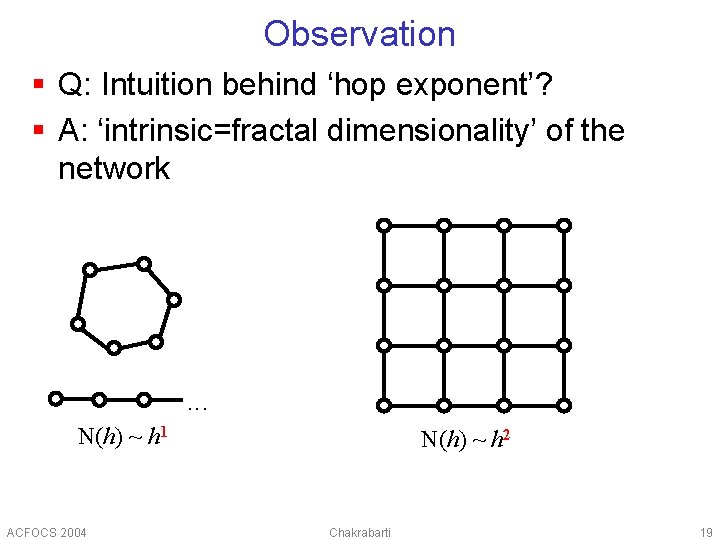
Observation § Q: Intuition behind ‘hop exponent’? § A: ‘intrinsic=fractal dimensionality’ of the network . . . N(h) ~ h 1 ACFOCS 2004 N(h) ~ h 2 Chakrabarti 19

Any other ‘laws’? § The Web looks like a “bow-tie” [Kumar+1999] § IN, SCC, OUT, ‘tendrils’ § Disconnected components ACFOCS 2004 Chakrabarti 20

Generators § How to generate graphs from a realistic distribution? § Difficulty: simultaneously preserving many local and global properties seen in realistic graphs § Erdos-Renyi: switch on each edge independently with some probability § Problem: degree distribution not power-law § Degree-based § Process-based (“preferential attachment”) ACFOCS 2004 Chakrabarti 21

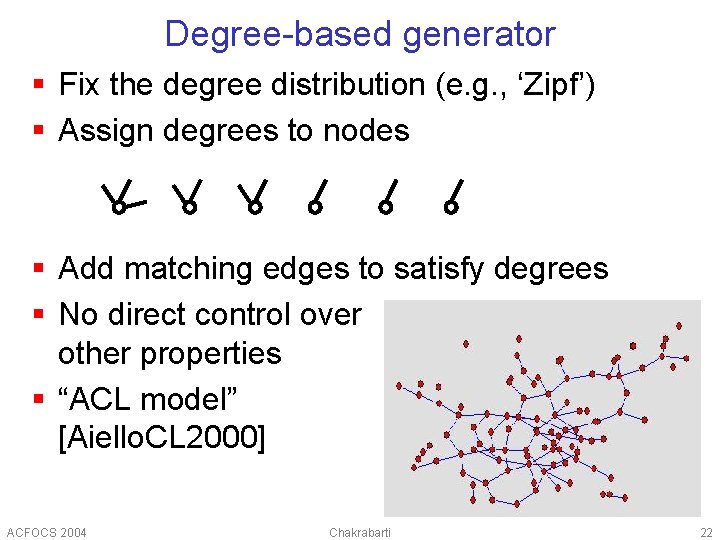
Degree-based generator § Fix the degree distribution (e. g. , ‘Zipf’) § Assign degrees to nodes § Add matching edges to satisfy degrees § No direct control over other properties § “ACL model” [Aiello. CL 2000] ACFOCS 2004 Chakrabarti 22

Process-based: Preferential attachment § § § Start with a clique with m nodes Add one node v at every time step v makes m links to old nodes Suppose old node u has degree d(u) Let pu = d(u)/ wd(w) v invokes a multinomial distribution defined by the set of p’s § And links to whichever u’s show up § At time t, there are m+t nodes, mt links § What is the degree distribution? ACFOCS 2004 Chakrabarti 23

Preferential attachment: analysis § § ki(t) = degree of node i at time t Discrete random variable Approximate as continuous random variable Let i(t) = E(ki(t)), expectation over random linking choices § At time t, the infinitesimal expected growth rate of i(t) is, by linearity of expectation, m degrees to add Total degree at t ACFOCS 2004 Time at which node i was born Chakrabarti 24

Preferential attachment, continued § Expected degree of each node grows as square-root of age: § Let the current time be t § A node must be old enough for its degree to be large; for i(t) > k, we need § Therefore, the fraction of nodes with degree larger than k is § Pr(degree = k) const/k 3 (data closer to 2) ACFOCS 2004 Chakrabarti 25

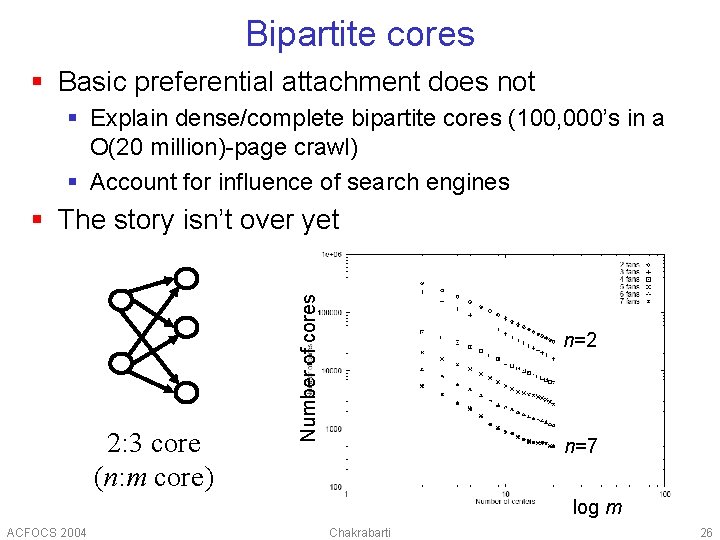
Bipartite cores § Basic preferential attachment does not § Explain dense/complete bipartite cores (100, 000’s in a O(20 million)-page crawl) § Account for influence of search engines 2: 3 core (n: m core) Number of cores § The story isn’t over yet n=2 n=7 log m ACFOCS 2004 Chakrabarti 26

Other process-based generators § “Copying model” [Kumar. RRTU 2000] § § New node v picks old reference node r u. a. r. v adds k new links to old nodes; for ith link: W. p. a add a link to an old node picked u. a. r. W. p. 1–a copy the ith link from r § More difficult to analyze § Reference node compression techniques! § H. O. T. : connect to closest, high-connectivity neighbor [Fabrikant+2002] § Winner does not take all [Pennock+2002] ACFOCS 2004 Chakrabarti 27

Reference-based graph compression § Well-motivated: pack graph into limited fast memory for, e. g. , query-time Web analysis § Standard approach § Assign integer IDs to URLs, lexicographic order § Delta or Gamma encoding of outlink IDs § If link-copying is rampant, should be able to compress Outlinks(u) by recording § A reference node r § Outlinks(r) Outlinks(u) …the “correction” § Finding r : what’s optimal? practical? [Adler, Mitzenmacher, Boldi, Vigna 2002— 2004] ACFOCS 2004 Chakrabarti 28

Reference-based compression, cont’d § r is a candidate reference for u if Outlinks(r) Outlinks(u) is “large enough” § Given G, construct G’ in which… § Directed edge from r to u with edge cost = number of bits needed to write down Outlinks(u) Outlinks(r) § Dummy node z, z has no outlinks in G § z connected to each u in G’ § cost(z, u) = #bits to write Outlinks(u) w/o ref § Shortest path tree rooted at z § In practice, pick “recent” r… 2. 58 bits/link ACFOCS 2004 Chakrabarti 29

log(count) Summary: Power laws are everywhere J. Ullman log(#citations) § § § log(freq) “a” “the ” log(rank) Bible: rank vs. word frequency Length of file transfers [Bestavros+] Web hit counts [Huberman] Click-stream data [Montgomery+01] Lotka’s law of publication count (Cite. Seer data) ACFOCS 2004 Chakrabarti 30

Resources § Generators § R-MAT deepay@cs. cmu. edu § BRITE www. cs. bu. edu/brite/ § INET topology. eecs. umich. edu/inet § Visualization tools § Graphviz www. graphviz. org § Pajek vlado. fmf. uni-lj. si/pub/networks/pajek § Kevin Bacon web site www. cs. virginia. edu/oracle § Erdös numbers etc. ACFOCS 2004 Chakrabarti 31

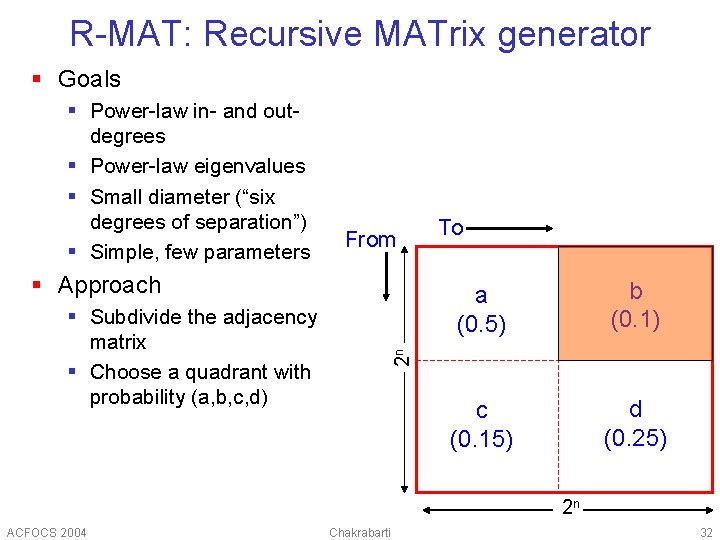
R-MAT: Recursive MATrix generator § Goals § Power-law in- and outdegrees § Power-law eigenvalues § Small diameter (“six degrees of separation”) § Simple, few parameters From § Subdivide the adjacency matrix § Choose a quadrant with probability (a, b, c, d) a (0. 5) b (0. 1) c (0. 15) d (0. 25) 2 n § Approach To 2 n ACFOCS 2004 Chakrabarti 32

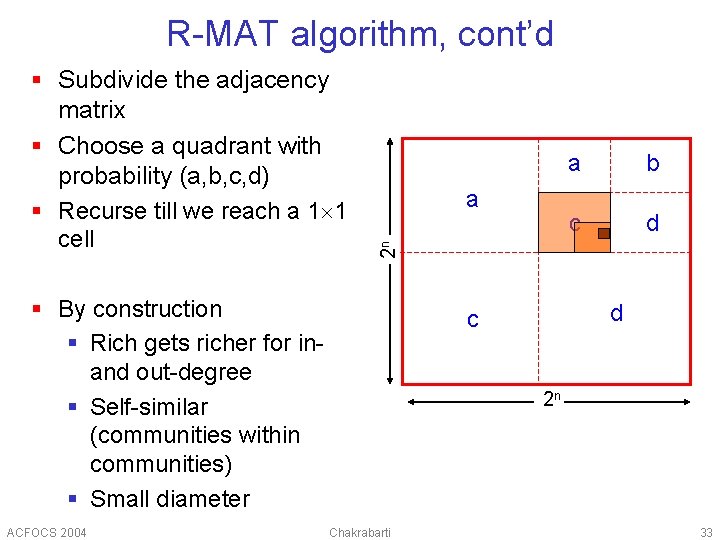
R-MAT algorithm, cont’d § Subdivide the adjacency matrix § Choose a quadrant with probability (a, b, c, d) § Recurse till we reach a 1 1 § By construction § Rich gets richer for inand out-degree § Self-similar (communities within communities) § Small diameter ACFOCS 2004 b c d 2 n cell a a d c 2 n Chakrabarti 33

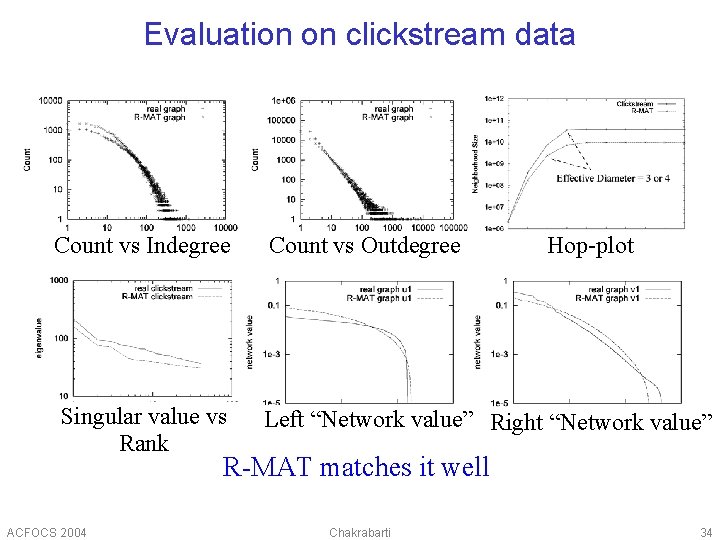
Evaluation on clickstream data Count vs Indegree Count vs Outdegree Hop-plot Singular value vs Rank Left “Network value” Right “Network value” R-MAT matches it well ACFOCS 2004 Chakrabarti 34

Topic structure of the Web § Measure correlations between link proximity and content similarity § How to characterize “topics”? Test doc § Started with http: //dmoz. org § Keep pruning until all leaf topics Classifier have enough (>300) samples § Approx 120 k sample URLs § Flatten to approx 482 topics § Train a text classifier § Characterize new document d as a vector of probabilities pd = (Pr(c|d) c) ACFOCS 2004 Chakrabarti 35

Sampling the background topic distrib. § What fraction of Web pages are about /Health/Diabetes? § How to sample the Web? § Invoke the “random surfer” model (Pagerank) § Walk from node to node § Sample trail adjusting for Pagerank § Modify Web graph to do better sampling § Self loops § Bidirectional edges ACFOCS 2004 Chakrabarti 36

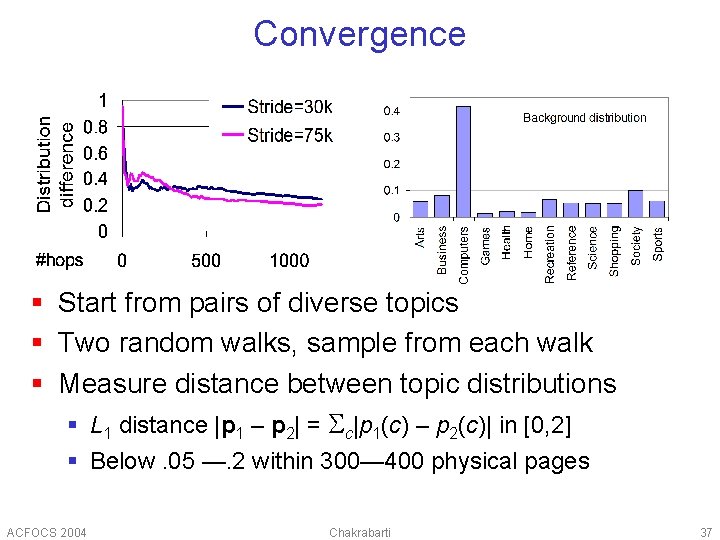
Convergence § Start from pairs of diverse topics § Two random walks, sample from each walk § Measure distance between topic distributions § L 1 distance |p 1 – p 2| = c|p 1(c) – p 2(c)| in [0, 2] § Below. 05 —. 2 within 300— 400 physical pages ACFOCS 2004 Chakrabarti 37

Biases in topic directories § Use Dmoz to train a classifier § Sample the Web § Classify samples § Diff Dmoz topic distribution from Web sample topic distribution § Report maximum deviation in fractions § NOTE: Not exactly Dmoz ACFOCS 2004 Chakrabarti 38

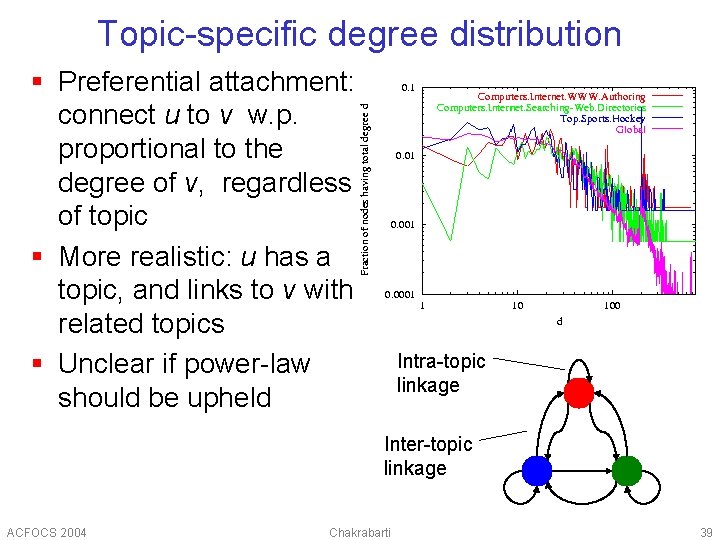
Topic-specific degree distribution § Preferential attachment: connect u to v w. p. proportional to the degree of v, regardless of topic § More realistic: u has a topic, and links to v with related topics § Unclear if power-law should be upheld Intra-topic linkage Inter-topic linkage ACFOCS 2004 Chakrabarti 39

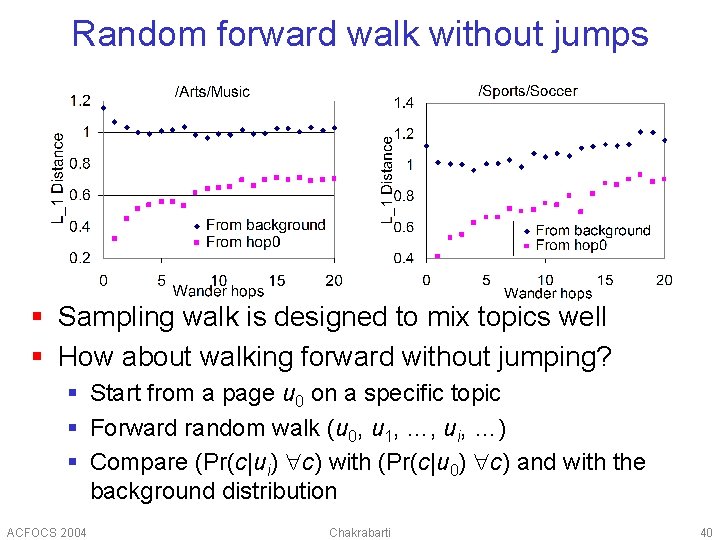
Random forward walk without jumps § Sampling walk is designed to mix topics well § How about walking forward without jumping? § Start from a page u 0 on a specific topic § Forward random walk (u 0, u 1, …, ui, …) § Compare (Pr(c|ui) c) with (Pr(c|u 0) c) and with the background distribution ACFOCS 2004 Chakrabarti 40

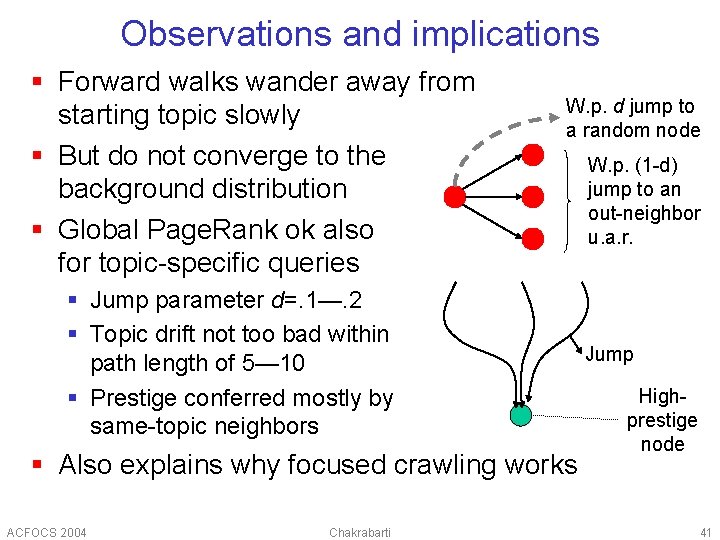
Observations and implications § Forward walks wander away from starting topic slowly § But do not converge to the background distribution § Global Page. Rank ok also for topic-specific queries W. p. d jump to a random node § Jump parameter d=. 1—. 2 § Topic drift not too bad within path length of 5— 10 § Prestige conferred mostly by same-topic neighbors § Also explains why focused crawling works ACFOCS 2004 Chakrabarti W. p. (1 -d) jump to an out-neighbor u. a. r. Jump Highprestige node 41

Citation matrix § Given a page is about topic i, how likely is it to link to topic j? § Matrix C[i, j] = probability that page about topic i links to page about topic j § Soft counting: C[i, j] += Pr(i|u)Pr(j|v) u § Applications v § Classifying Web pages into topics § Focused crawling for topic-specific pages § Finding relations between topics in a directory ACFOCS 2004 Chakrabarti 42

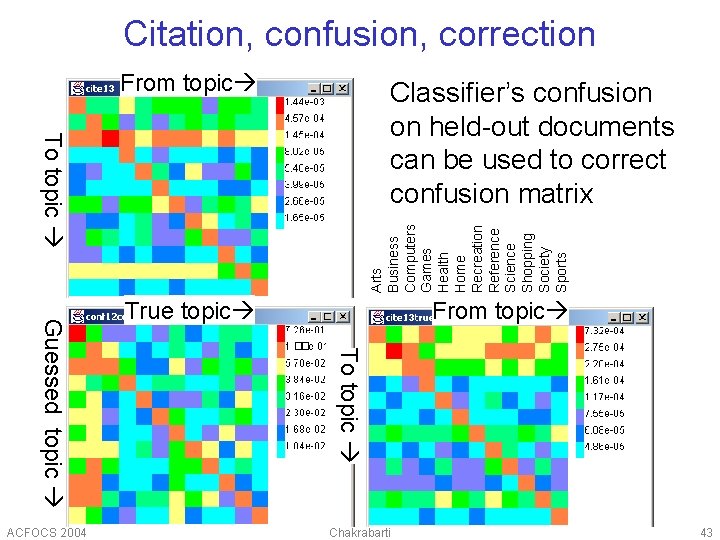
Citation, confusion, correction From topic True topic From topic To topic Guessed topic ACFOCS 2004 Arts Business Computers Games Health Home Recreation Reference Science Shopping Society Sports To topic Classifier’s confusion on held-out documents can be used to correct confusion matrix Chakrabarti 43

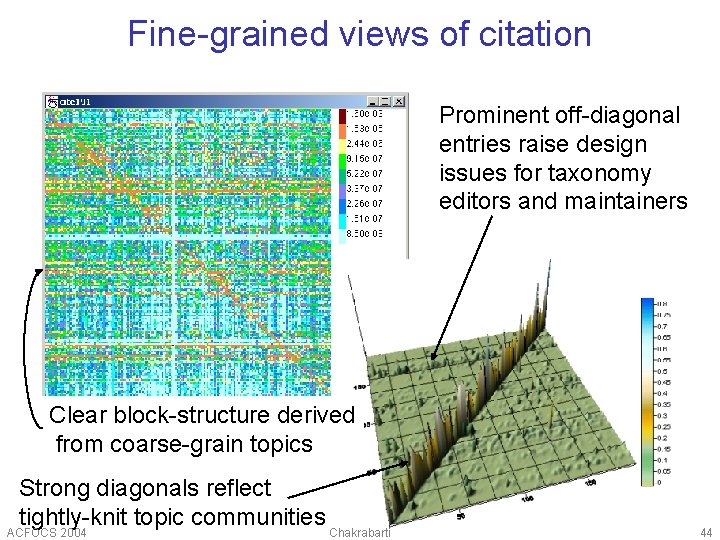
Fine-grained views of citation Prominent off-diagonal entries raise design issues for taxonomy editors and maintainers Clear block-structure derived from coarse-grain topics Strong diagonals reflect tightly-knit topic communities ACFOCS 2004 Chakrabarti 44

Outline, some more detail § Part 1 (Modeling graphs) § What do real-life graphs look like? § What laws govern their formation, evolution and properties? § What structural analyses are useful? § Part 2 (Analyzing graphs) § § ACFOCS 2004 Modeling data analysis problems using graphs Proposing parametric models Estimating parameters Applications from Web search and text mining Chakrabarti 45

Centrality and prestige ACFOCS 2004 Chakrabarti 46

How important is a node? § § § § Degree, min-max radius, … Pagerank Maximum entropy network flows HITS and stochastic variants Stability and susceptibility to spamming Hypergraphs and nonlinear systems Using other hypertext properties Applications: Ranking, crawling, clustering, detecting obsolete pages ACFOCS 2004 Chakrabarti 47

Importance/prestige as Pagerank § A node is important if it is connected to important nodes § “Random surfer” walks along links for ever § If current node has 3 outlinks, take each with probability 1/3 § Importance = steady-state u probability (ssp) of visit v Out. Degree(u)=3 § “Maxwell’s equation for the Web” ACFOCS 2004 Chakrabarti 48

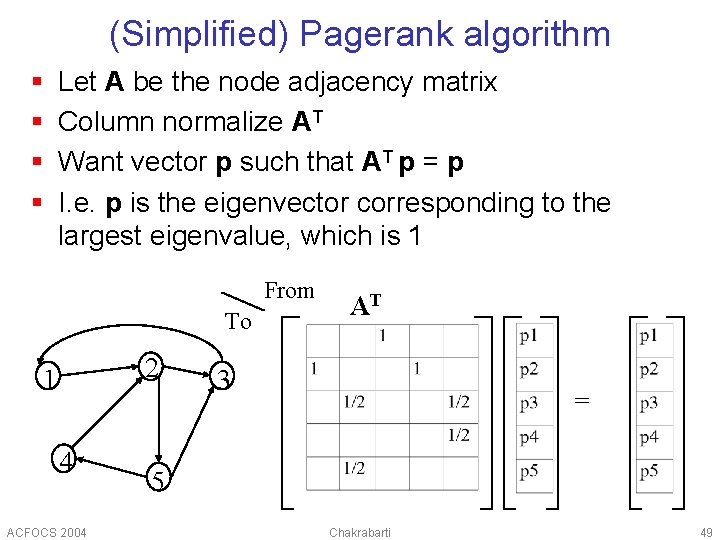
(Simplified) Pagerank algorithm § § Let A be the node adjacency matrix Column normalize AT Want vector p such that AT p = p I. e. p is the eigenvector corresponding to the largest eigenvalue, which is 1 From To 2 1 4 ACFOCS 2004 AT 3 = 5 Chakrabarti 49

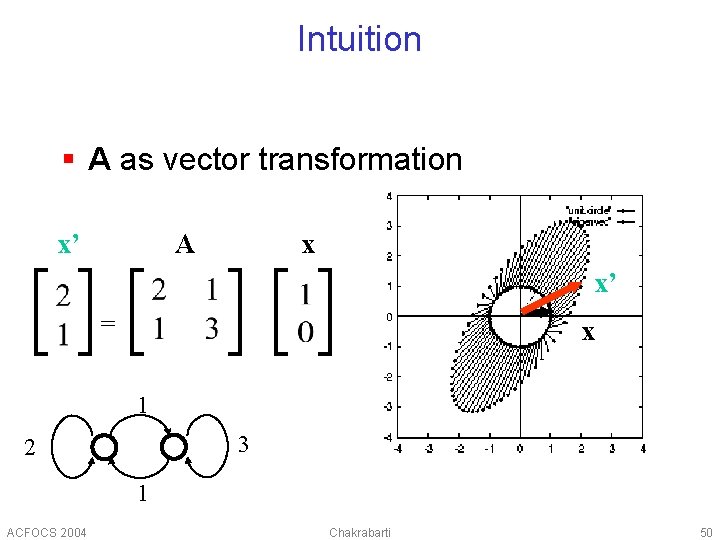
Intuition § A as vector transformation x’ x A x’ = x 1 3 2 1 ACFOCS 2004 Chakrabarti 50

Intuition § By defn. , eigenvectors remain parallel to themselves (‘fixed points’) 1 3. 62 * ACFOCS 2004 v 1 A v 1 = Chakrabarti 51

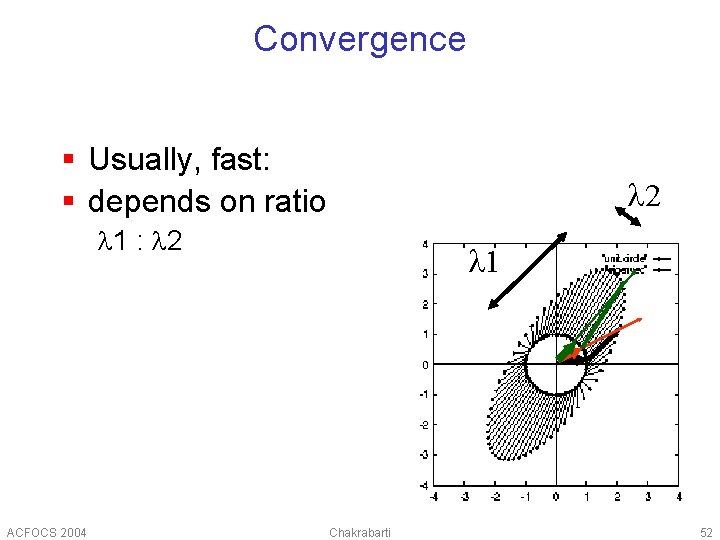
Convergence § Usually, fast: § depends on ratio 2 1 : 2 ACFOCS 2004 1 Chakrabarti 52

Eigenvalues and epidemic networks § Will a virus spread across an arbitrary network create an epidemic? § Susceptible-Infected-Susceptible (SIS) § § Was healthy, did not got infected Was infected, got cured without further attack Was infected, got cured immediately after attack Cured nodes immediately become susceptible Infected by neighbor Susceptible/ healthy ACFOCS 2004 Cured internally Chakrabarti Infected & infectious 53

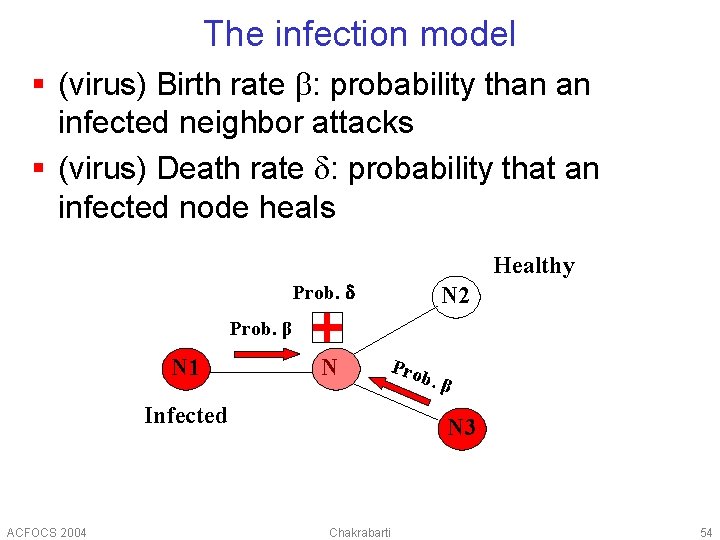
The infection model § (virus) Birth rate b: probability than an infected neighbor attacks § (virus) Death rate d: probability that an infected node heals Healthy Prob. d N 2 Prob. β N 1 N Pro Infected ACFOCS 2004 b. β N 3 Chakrabarti 54

Working parameters § pi, t = prob. node i is infected at time t Prob. that node i does NOT receive an infection from neighbors § Was healthy, did not got infected § Was infected, got cured without further attack § Was infected, got attacks from neighbors and yet cured itself in this time step … somewhat arbitrary ACFOCS 2004 Chakrabarti 55

Time recurrence for pi, t § Assuming various probabilities are “suitably small” § Recurrence of the probability of infection can be approximated by this linear form: § In other words, the (symmetric) transition matrix is ACFOCS 2004 Chakrabarti 56

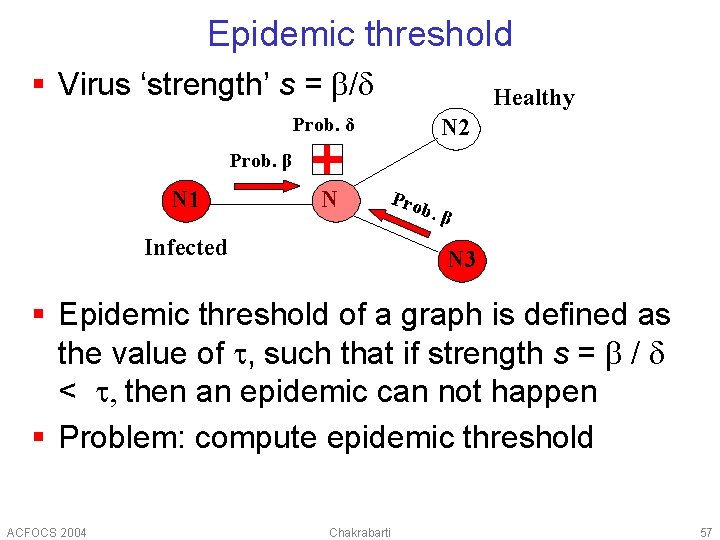
Epidemic threshold § Virus ‘strength’ s = b/d Healthy Prob. δ N 2 Prob. β N 1 N Pro Infected b. β N 3 § Epidemic threshold of a graph is defined as the value of t, such that if strength s = b / d < t, then an epidemic can not happen § Problem: compute epidemic threshold ACFOCS 2004 Chakrabarti 57

Epidemic threshold t What should t depend on? § avg. degree? and/or highest degree? § and/or variance of degree? § and/or third moment of degree? ACFOCS 2004 Chakrabarti 58

Analysis § Eigenvectors of S and A are the same § Eigenvalues are shifted and scaled § From spectral decomposition § A sufficient condition for infection dying down is that ACFOCS 2004 Chakrabarti 59

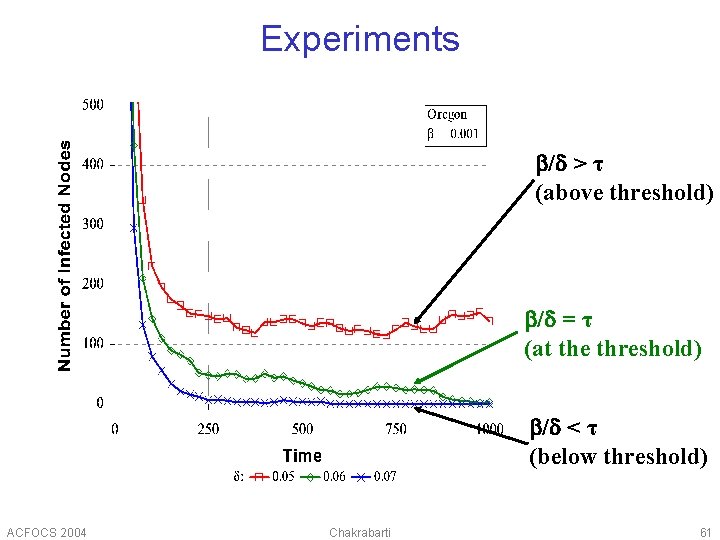
Epidemic threshold § An epidemic must die down if epidemic threshold recovery prob. β/δ <τ = 1/ λ 1, A attack prob. largest eigenvalue of adj. matrix A Proof: [Wang+03] ACFOCS 2004 Chakrabarti 60

Experiments b/d > τ (above threshold) b/d = τ (at the threshold) b/d < τ (below threshold) ACFOCS 2004 Chakrabarti 61

Remarks § “Primal” problem: topology design § Design a network resilient to infection § “Dual” problem: viral marketing § Selectively convert important customers who can influence many others § Will come back to this later ACFOCS 2004 Chakrabarti 62

Back to the random surfer § Practical issues with Pagerank [Brin. P 1997] § PR converges only if E is aperiodic and irreducible; make it so: § d is the (tuned) probability of “teleporting” to one of N pages uniformly at random (0. 1— 0. 2 in practice) § (Possibly) unintended consequences: topic sensitivity, stability ACFOCS 2004 Chakrabarti 63

Prestige as network flow § § § yij =#surfers clicking from i to j per unit time Hits per unit time on page j is Flow is conserved at The total traffic is Normalize: Can interpret pij as a probability § Standard Pagerank corresponds to one solution: § Many other solutions possible ACFOCS 2004 Chakrabarti 64

Maximum entropy flow [Tomlin 2003] § Flow conservation modeled using feature § And the constraints § Goal is to maximize subject to § Solution has form § i is the “hotness” of page i ACFOCS 2004 Chakrabarti 65

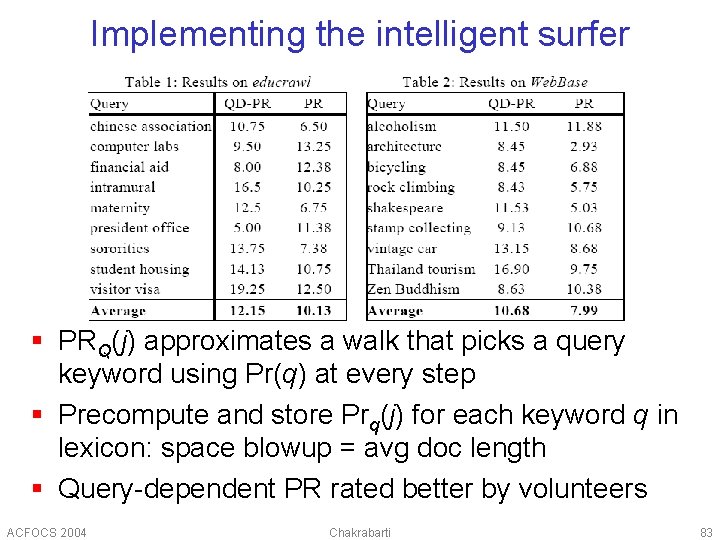
Maxent flow results i ranking is better than Pagerank; Hi ranking is worse Two IBM intranet data sets with known top URLs Average rank (106) of known top URLs when sorted by Pagerank Depth up to which dmoz. org URLs are used as ground truth Hi i (Smaller rank is better) Average rank (108) ACFOCS 2004 Chakrabarti 66

HITS [Kleinberg 1997] § Two kinds of prestige § Good hubs link to good authorities § Good authorities are linked to by good hubs § In matrix notation, iterations amount to with interleaved normalization of h and a § Note that scores are copied not divided ACFOCS 2004 Chakrabarti 67

HITS graph acquisition § Steps § Get root set via keyword query § Expand by one move forward and backward § Drop same-site links (why? ) § Each node assigned both a hub and an auth score § Graph tends to be “topicspecific” IN Root set § Whereas Pagerank is usually run on “the entire Web” (but need not be) ACFOCS 2004 Chakrabarti OUT 68

HITS vs. Pagerank, more comments § Dominant eigenvectors of different matrices § HITS: Eigensystems of EET (h) and ETE (a) § Pagerank: eigensystem of where § HITS copies scores, Pagerank distributes § HITS drops same-site links, Pagerank does (can? ) not § Implications? ACFOCS 2004 Chakrabarti 69

HITS: Dyadic interpretation [Cohn. C 2000] § Graph includes many communities z § Query=“Jaguar” gets auto, game, animal links § Each URL is represented as two things § A document d § A citation c § Max § Guess number of aspects zs and use [Hofmann 1999] to estimate Pr(c|z) § These are the most authoritative URLs ACFOCS 2004 Chakrabarti 70

Dyadic results for “Machine learning” Clustering based on citations + ranking within clusters ACFOCS 2004 Chakrabarti 71

Spamming link-based ranking § Recipe for spamming HITS § Create a hub linking to genuine authorities § Then mix in links to your customers’ sites § Highly susceptible to adversarial behavior § Recipe for spamming Pagerank § Buy a bunch of domains, cloak IP addresses § Host a site at each domain § Sprinkle a few links at random per page to other sites you own § Takes more work than spamming HITS ACFOCS 2004 Chakrabarti 72

§ Why? § How to design more stable algorithms? ACFOCS 2004 Chakrabarti Pagerank § Compute HITS authority scores and Pagerank § Delete 30% of nodes/links at random § Recompute and compare ranks; repeat § Pageranks more stable than HITS authority ranks HITS Authority Stability of link analysis [Ng. ZJ 2001] 73

Stability depends on graph and params § Auth score is eigenvector for ETE = S, say § Let 1 > 2 be the first two eigenvalues § There exists an S’ such that § S and S’ are close ||S–S’||F = O( 1 – 2) § But ||u 1 – u’ 1||2 = (1) § Pagerank p is eigenvector of § U is a matrix full of 1/N and is the jump prob § If set C of nodes are changed in any way, the new Pagerank vector p’ satisfies ACFOCS 2004 Chakrabarti 74

Randomized HITS § Much more stable than HITS § Results more meaningful § near 1 will always stabilize § Here was 0. 2 ACFOCS 2004 Chakrabarti Pagerank Randomized HITS § Each half-step, with probability , teleport to a node chosen uniformly at random 75

Another random walk variation of HITS § SALSA: Stochastic HITS [Lempel+2000] § Two separate random walks 1/3 a 1 § From authority to authority via hub 1/3 § From hub to hub via authority 1/3 § Transition probability Pr(ai aj) = 1/2 a 2 1/2 § If transition graph is irreducible, § For disconnected components, depends on relative size of bipartite cores § Avoids dominance of larger cores ACFOCS 2004 Chakrabarti 76

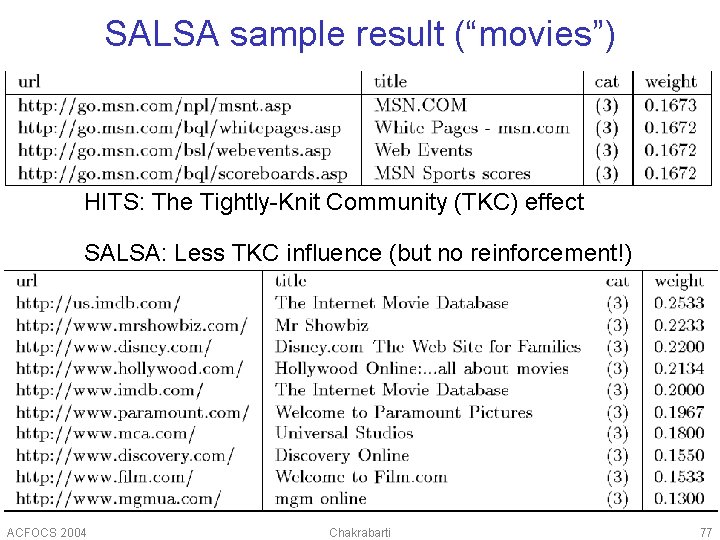
SALSA sample result (“movies”) HITS: The Tightly-Knit Community (TKC) effect SALSA: Less TKC influence (but no reinforcement!) ACFOCS 2004 Chakrabarti 77

Links in relational data [Gibson. KR 1998] § (Attribute, value) pair is a node § Each node v has weight wv § Each tuple is a hyperedge § Tuple r has weight xr § HITS-like iterations to update weight wv § For each tuple § Update weight § Combining operator can be sum, max, product, Lp avg, etc. ACFOCS 2004 Chakrabarti 78

Database Theory Distilling links in relational data ACFOCS 2004 Author Chakrabarti Forum Year 79

Searching and annotating graph data ACFOCS 2004 Chakrabarti 80

Searching graph data § Nodes in graph contain text § Random Intelligent surfer [Richardson. D 2001] § Topic-sensitive Pagerank [Haveliwala 2002] § Assigning image captions using random walks [Pan. YFD 2004] § Rotting pages and links [Bar. Yossef. BKT 2004] § Query is a set of keywords § All keywords may not match a single node § Implicit joins [Hulgeri+2001, Agrawal+2002] § Or rank aggregation [Balmin+2004] required ACFOCS 2004 Chakrabarti 81

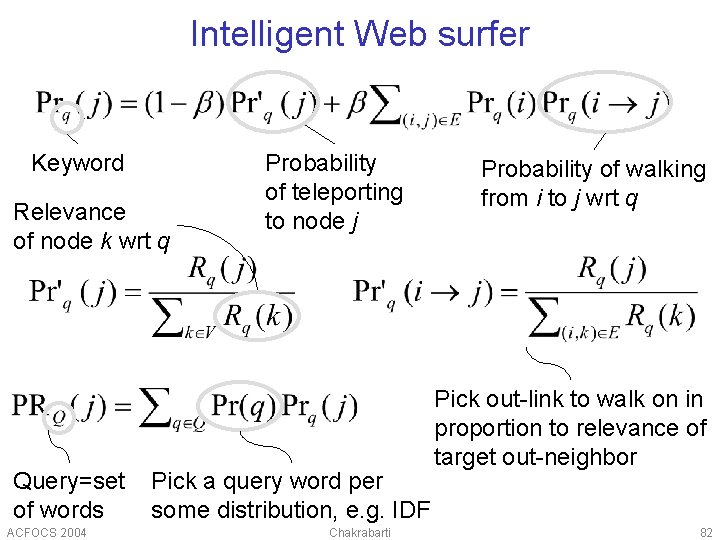
Intelligent Web surfer Keyword Relevance of node k wrt q Query=set of words ACFOCS 2004 Probability of teleporting to node j Pick a query word per some distribution, e. g. IDF Chakrabarti Probability of walking from i to j wrt q Pick out-link to walk on in proportion to relevance of target out-neighbor 82

Implementing the intelligent surfer § PRQ(j) approximates a walk that picks a query keyword using Pr(q) at every step § Precompute and store Prq(j) for each keyword q in lexicon: space blowup = avg doc length § Query-dependent PR rated better by volunteers ACFOCS 2004 Chakrabarti 83

Topic-sensitive Pagerank § High overhead for per-word Pagerank § Instead, compute Pageranks for some collection of broad topics PRc(j) § Topic c has sample page set Sc § Walk as in Pagerank § Jump to a node in Sc uniformly at random § “Project” query onto set of topics § Rank responses by projection-weighted Pageranks ACFOCS 2004 Chakrabarti 84

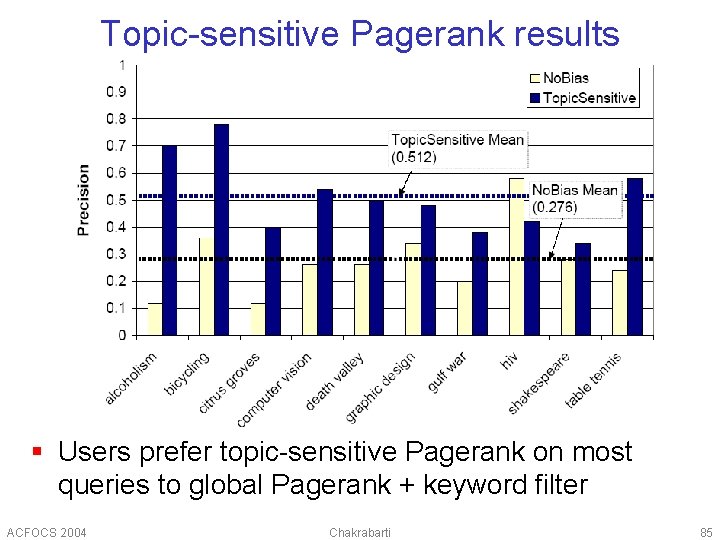
Topic-sensitive Pagerank results § Users prefer topic-sensitive Pagerank on most queries to global Pagerank + keyword filter ACFOCS 2004 Chakrabarti 85

Image captioning § Segment images into regions § Image has caption words § Three-layer graph: image, regions, caption words § Threshold on region similarity to connect regions (dotted) ACFOCS 2004 Chakrabarti 86

Random walks with restarts Regions Test image Images Words § Find regions in test image § Connect regions to other nodes in the region layer using region similarity § Random walk, restarting at test image node § Pick words with largest visit probability ACFOCS 2004 Chakrabarti 87

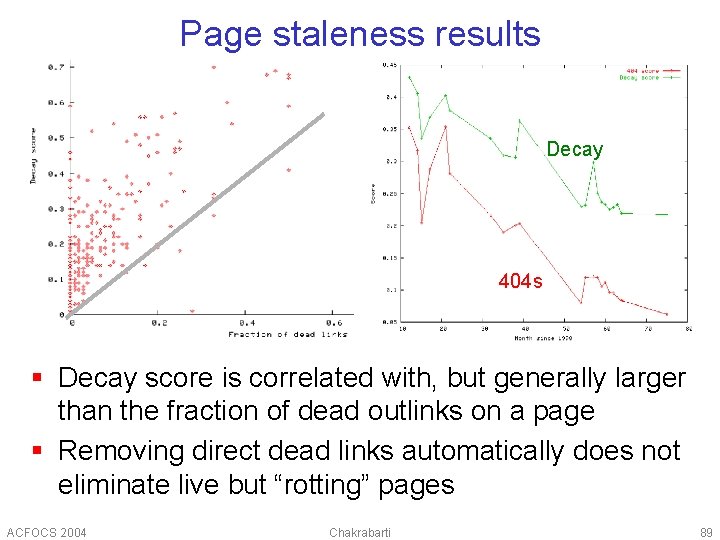
More random walks: “Link rot” § How stale is a page? § Last-mod unreliable § Automatic dead-link cleaners mask disuse § A page is “completely stale” if it is “dead” § Let D be the set of pages which cannot be accessed (404 and other problems) § How stale is a page u? Start with p u § If p D declare decay value of u to be 1, else § With probability declare decay value of u = 0 § W. p. 1– choose outlink v, set p v, loop ACFOCS 2004 Chakrabarti 88

Page staleness results Decay 404 s § Decay score is correlated with, but generally larger than the fraction of dead outlinks on a page § Removing direct dead links automatically does not eliminate live but “rotting” pages ACFOCS 2004 Chakrabarti 89

Graph proximity search: two paradigms § A single node as query response § Find node that matches query terms… § …or is “near” nodes matching query terms [Goldman+ 1998] § A connected subgraph as query response § Single node may not match all keywords § No natural “page boundary” [Bhalotia+2002] [Agrawal+2002] ACFOCS 2004 Chakrabarti 90

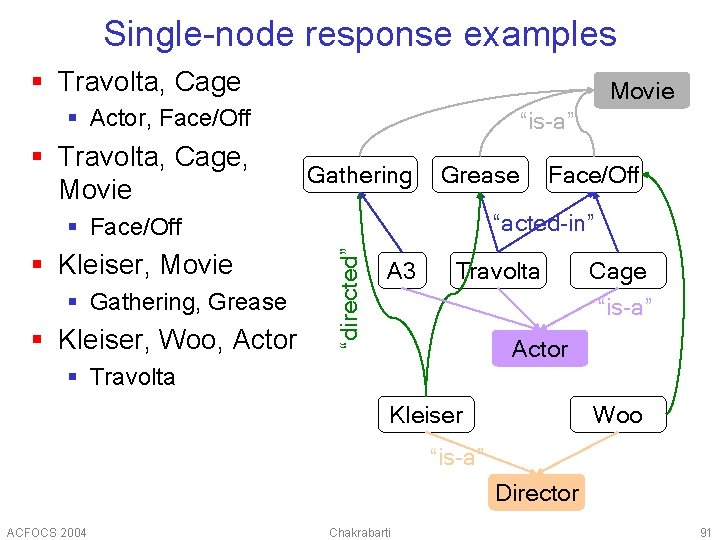
Single-node response examples § Travolta, Cage Movie § Actor, Face/Off § Travolta, Cage, Movie “is-a” Gathering Grease “acted-in” § Gathering, Grease § Kleiser, Woo, Actor “directed” § Face/Off § Kleiser, Movie Face/Off A 3 Travolta Cage “is-a” Actor § Travolta Kleiser Woo “is-a” Director ACFOCS 2004 Chakrabarti 91

Basic search strategy § Node subset A activated because they match query keyword(s) § Look for node near nodes that are activated § Goodness of response node depends § Directly on degree of activation § Inversely on distance from activated node(s) ACFOCS 2004 Chakrabarti 92

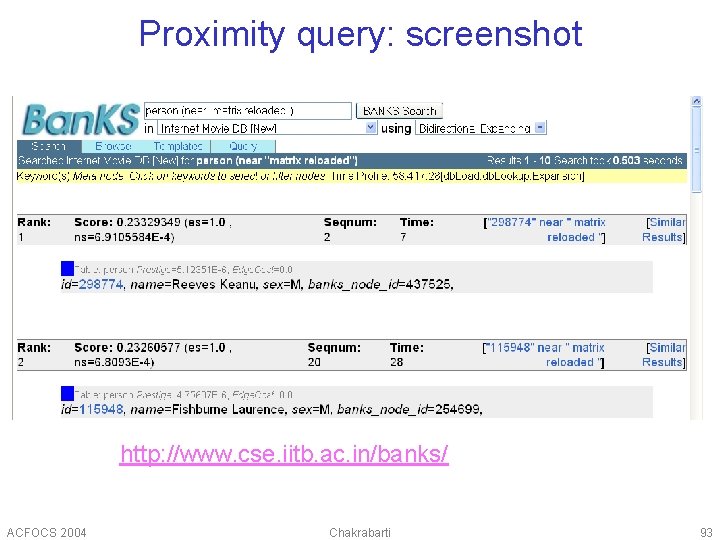
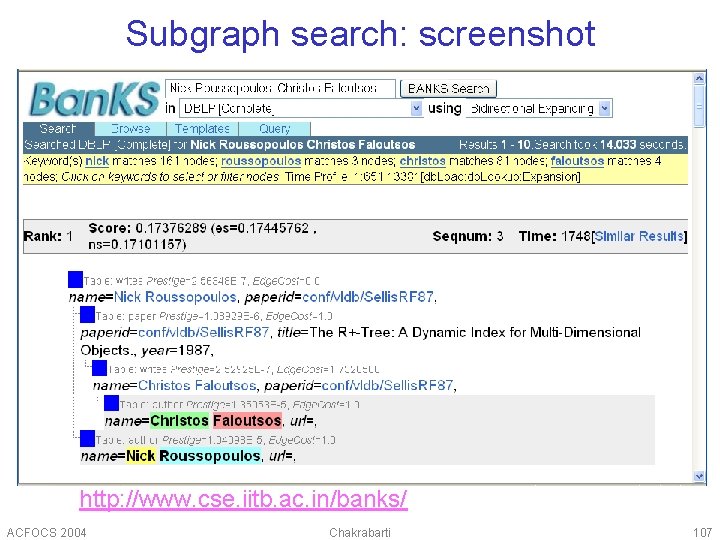
Proximity query: screenshot http: //www. cse. iitb. ac. in/banks/ ACFOCS 2004 Chakrabarti 93

Ranking a single node response § Activated node set A § Rank node r in “response set” R based on proximity to nodes a in A § Nodes have relevance R and A in [0, 1] § Edge costs are “specified by the system” § d(a, r) = cost of shortest path from a to r § Bond between a and r § Parameter t tunes relative emphasis on distance and relevance score § Several ad-hoc choices ACFOCS 2004 Chakrabarti 94

Scoring single response nodes § Additive § Belief § Goal: list a limited number of find nodes with the largest scores § Performance issues § Assume the graph is in memory? § Precompute all-pairs shortest path (|V |3)? § Prune unpromising candidates? ACFOCS 2004 Chakrabarti 95

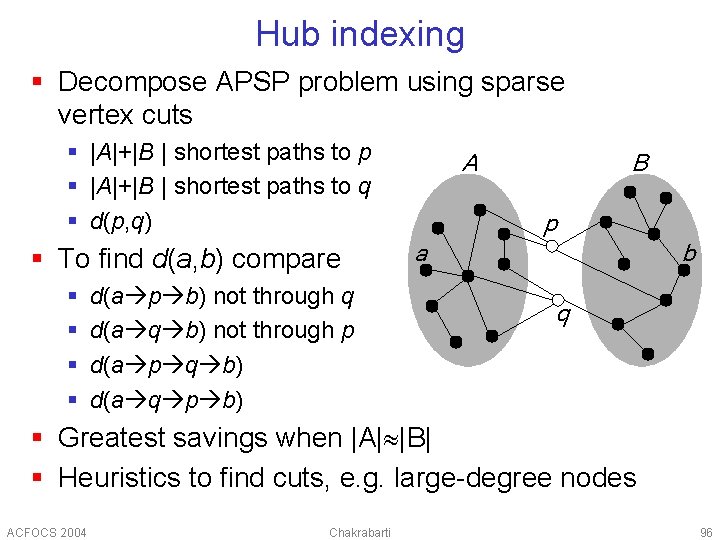
Hub indexing § Decompose APSP problem using sparse vertex cuts § |A|+|B | shortest paths to p § |A|+|B | shortest paths to q § d(p, q) § To find d(a, b) compare § § d(a p b) not through q d(a q b) not through p d(a p q b) d(a q p b) A B p a b q § Greatest savings when |A| |B| § Heuristics to find cuts, e. g. large-degree nodes ACFOCS 2004 Chakrabarti 96

Object. Rank [Balmin+2004] § Given a data graph with nodes having text § For each keyword precompute a keywordsensitive Pagerank [Richardson. D 2001] § Score of a node for multiple keyword search based on fuzzy AND/OR § Approximation to Pagerank of node with restarts to nodes matching keywords § Use Fagin-merge [Fagin 2002] to get best nodes in data graph ACFOCS 2004 Chakrabarti 97

Connected subgraph as response § Single node may not match all keywords § No natural “page boundary” § On-the-fly joins make up a “response page” § Two scenarios § Keyword search on relational data • Keywords spread among normalized relations § Keyword search on XML-like or Web data • Keywords spread among DOM nodes and subtrees ACFOCS 2004 Chakrabarti 98

Keyword search on relational data § Tuple = node § Some columns have text § Foreign key constraints = edges in schema graph § Query = set of terms § No natural notion of a document Cites Citing Cited Author. ID Author. Name Paper. ID Paper. Name Writes Author. ID Paper. ID § Normalization § Join may be needed to generate results § Cycles may exist in schema graph: ‘Cites’ ACFOCS 2004 Chakrabarti 99

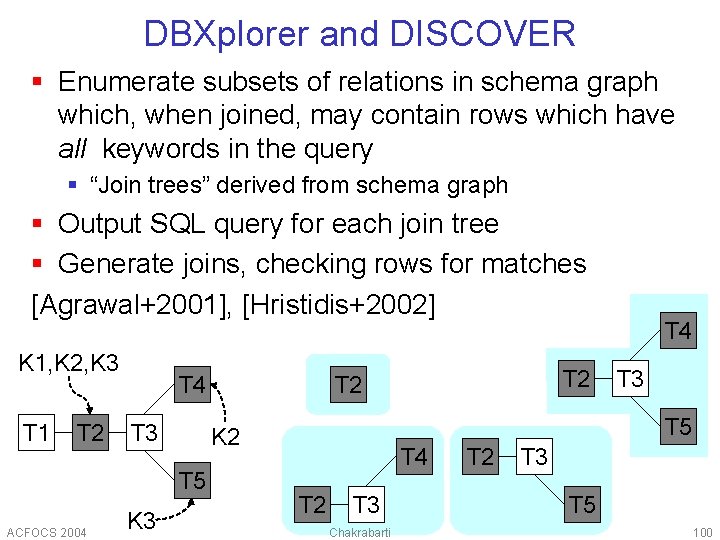
DBXplorer and DISCOVER § Enumerate subsets of relations in schema graph which, when joined, may contain rows which have all keywords in the query § “Join trees” derived from schema graph § Output SQL query for each join tree § Generate joins, checking rows for matches [Agrawal+2001], [Hristidis+2002] K 1, K 2, K 3 T 1 T 2 T 4 T 3 ACFOCS 2004 K 3 T 5 K 2 T 5 T 2 T 4 T 2 T 3 Chakrabarti T 2 T 3 T 5 100

Discussion C Exploits relational schema information to contain search C Pushes final extraction of joined tuples into RDBMS C Faster than dealing with full data graph directly ACFOCS 2004 D Coarse-grained ranking based on schema tree D Does not model proximity or (dis) similarity of individual tuples D No recipe for data with less regular (e. g. XML) or ill-defined schema Chakrabarti 101

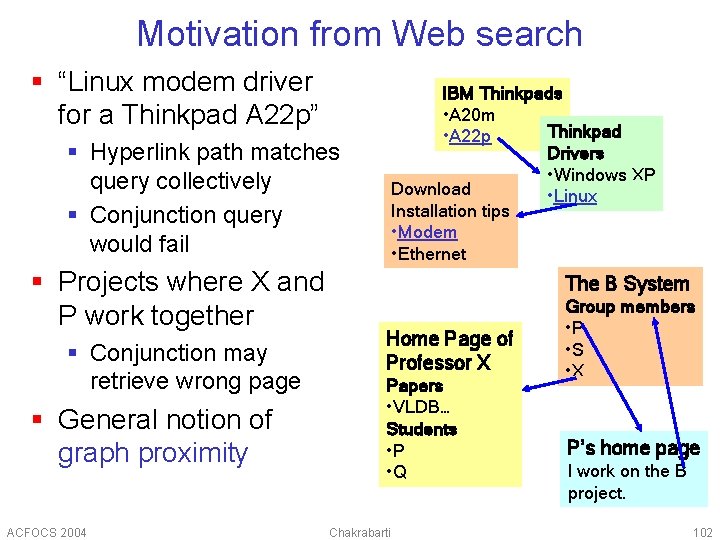
Motivation from Web search § “Linux modem driver for a Thinkpad A 22 p” IBM Thinkpads • A 20 m Thinkpad • A 22 p Drivers • Windows XP Download • Linux Installation tips • Modem • Ethernet § Hyperlink path matches query collectively § Conjunction query would fail § Projects where X and P work together § Conjunction may retrieve wrong page § General notion of graph proximity ACFOCS 2004 The B System Home Page of Professor X Papers • VLDB… Students • P • Q Chakrabarti Group members • P • S • X P’s home page I work on the B project. 102

Data structures for search § Answer = tree with at least one leaf containing each keyword in query § Group Steiner tree problem, NP-hard § Query term t found in source nodes St § Single-source-shortest-path SSSP iterator § Initialize with a source (near-) node § Consider edges backwards § get. Next() returns next nearest node § For each iterator, each visited node v maintains for each t a set v. Rt of nodes in St which have reached v ACFOCS 2004 Chakrabarti 103

Generic expanding search § Near node sets St with S = t St § For all source nodes S § create a SSSP iterator with source § While more results required § § Get next iterator and its next-nearest node v Let t be the term for the iterator’s source s cross. Product = {s} t ’ tv. Rt’ For each tuple of nodes in cross. Product • Create an answer tree rooted at v with paths to each source node in the tuple § Add s to v. Rt ACFOCS 2004 Chakrabarti 104

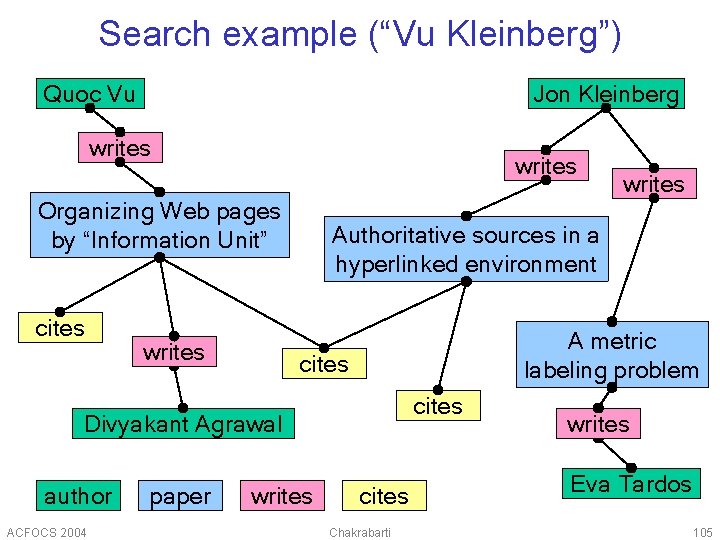
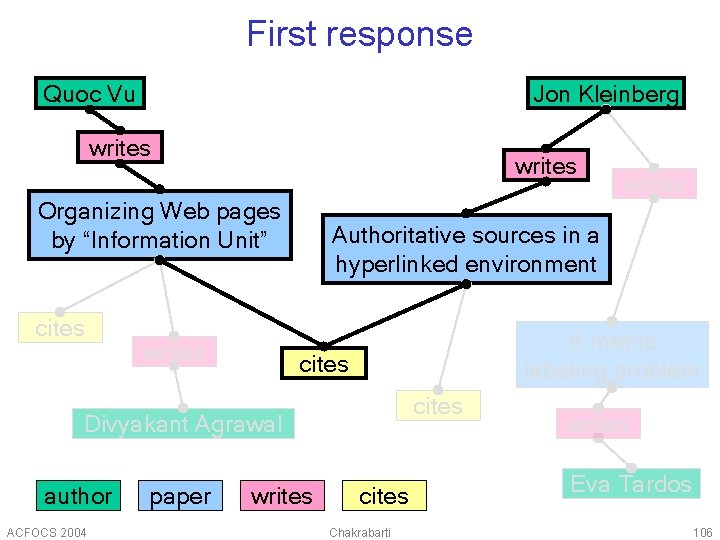
Search example (“Vu Kleinberg”) Quoc Vu Jon Kleinberg writes Organizing Web pages by “Information Unit” cites writes Authoritative sources in a hyperlinked environment A metric labeling problem cites Divyakant Agrawal author ACFOCS 2004 paper writes cites Chakrabarti writes Eva Tardos 105

First response Quoc Vu Jon Kleinberg writes Organizing Web pages by “Information Unit” cites writes Authoritative sources in a hyperlinked environment A metric labeling problem cites Divyakant Agrawal author ACFOCS 2004 paper writes cites Chakrabarti writes Eva Tardos 106

Subgraph search: screenshot http: //www. cse. iitb. ac. in/banks/ ACFOCS 2004 Chakrabarti 107

Similarity, neighborhood, influence ACFOCS 2004 Chakrabarti 108

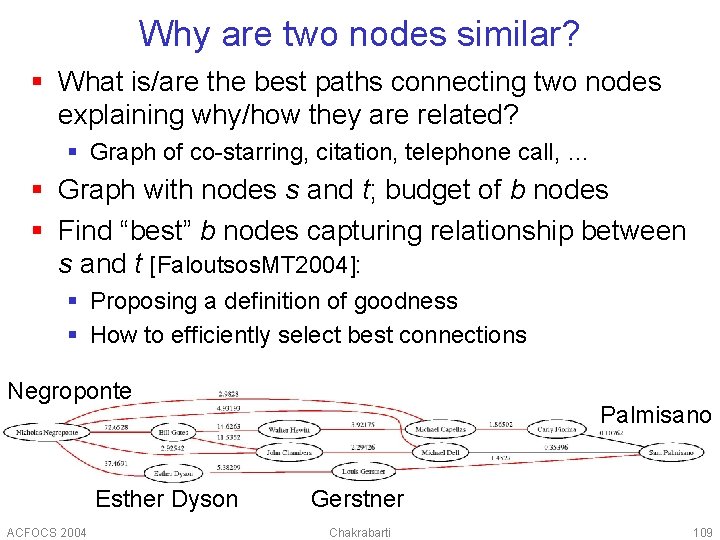
Why are two nodes similar? § What is/are the best paths connecting two nodes explaining why/how they are related? § Graph of co-starring, citation, telephone call, … § Graph with nodes s and t; budget of b nodes § Find “best” b nodes capturing relationship between s and t [Faloutsos. MT 2004]: § Proposing a definition of goodness § How to efficiently select best connections Negroponte Esther Dyson ACFOCS 2004 Palmisano Gerstner Chakrabarti 109

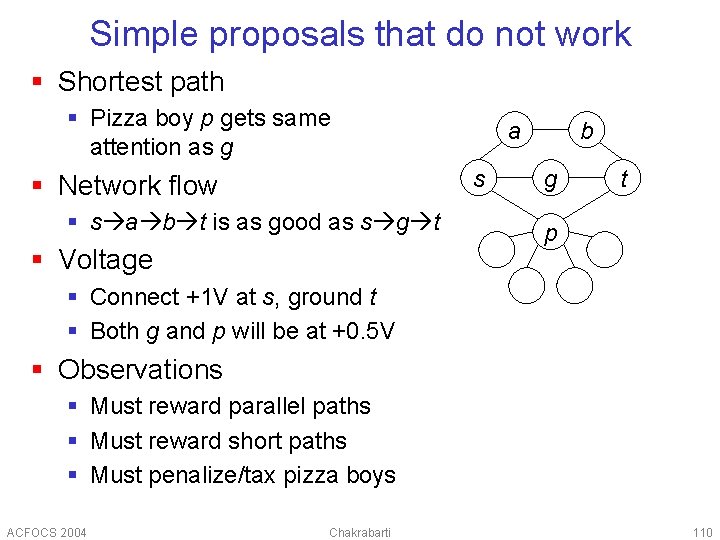
Simple proposals that do not work § Shortest path § Pizza boy p gets same attention as g a s § Network flow § s a b t is as good as s g t § Voltage b g t p § Connect +1 V at s, ground t § Both g and p will be at +0. 5 V § Observations § Must reward parallel paths § Must reward short paths § Must penalize/tax pizza boys ACFOCS 2004 Chakrabarti 110

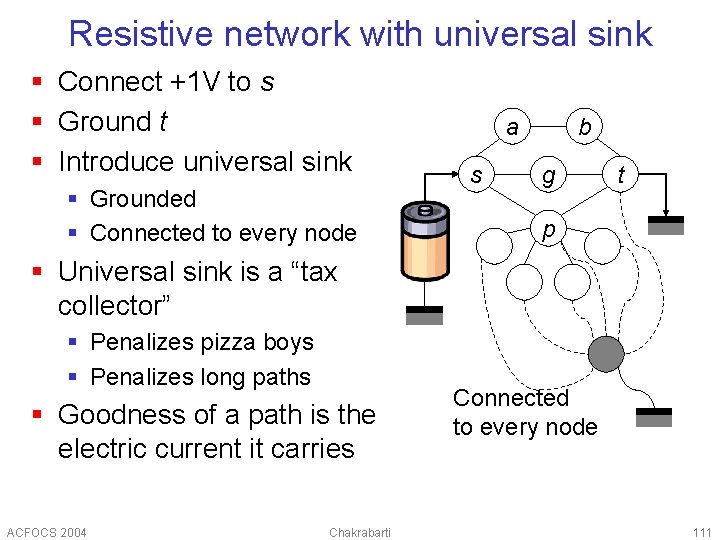
Resistive network with universal sink § Connect +1 V to s § Ground t § Introduce universal sink § Grounded § Connected to every node a s b g t p § Universal sink is a “tax collector” § Penalizes pizza boys § Penalizes long paths § Goodness of a path is the electric current it carries ACFOCS 2004 Chakrabarti Connected to every node 111

Resistive network algorithm § § Ohm’s law: Kirchhoff’s current law: Boundary conditions (without sink): Solution: § § Here C(u, v) is the conductance from u to v Add grounded universal sink z with V(z)=0 Set Display subgraph carrying high current ACFOCS 2004 Chakrabarti 112

Distributions influenced via graphs § Directed or undirected graph; nodes have § Observable properties § Some unobservable (random) state § Edges indicate that distributions over unobservable states are coupled § Many applications § § ACFOCS 2004 Hypertext classification (topics are clustered) Social network of customers buying products Hierarchical classification Labeling categorical sequences: pos/ne tagging, sense disambiguation, linkage analysis Chakrabarti 113

Basic techniques § Directed (acyclic) graphs: Bayesian network § Markov networks § (Loopy) belief propagation § Conditional Markov networks § Avoid modeling joint distribution over observable and hidden properties of nodes § Some computationally simple special cases ACFOCS 2004 Chakrabarti 114

Hypertext classification § Want to assign labels to Web pages § Text on a single page may be too little or misleading § Page is not an isolated instance by itself § Problem setup § § § Web graph G=(V, E) Node u V is a page having text u. T Edges in E are hyperlinks Some nodes are labeled Make collective guess at missing labels § Probabilistic model? Benefits? ACFOCS 2004 Chakrabarti 115

Graph labeling model § Seek a labeling f of all unlabeled nodes so as to maximize Luckily we don’t need to worry about this § Let VK be the nodes with known labels and f(VK) their known label assignments § Let N(v) be the neighbors of v and NK(v) N(v) be neighbors with known labels § Markov assumption: f(v) is conditionally independent of rest of G given f(N(v)) ACFOCS 2004 Chakrabarti 116

Markov graph labeling Probability of labeling specific node v… …given edges, text, parital labeling Sum over all possible labelings of unknown neighbors of v Markov assumption: label of v does not depend on unknown labels outside the set NU(v) § Circularity between f(v) and f(NU(v)) § Some form of iterative Gibb’s sampling or MCMC ACFOCS 2004 Chakrabarti 117

Iterative labeling Label estimates of v in the next iteration Joint distribution over neighbors approximated as product of marginals Take the expectation of this term over NU(v) labelings § Sum over all possible NU(v) labelings still too expensive to compute § In practice, prune to most likely configurations § Let us look at the last term more carefully ACFOCS 2004 Chakrabarti 118

A generative node model By the Markov assumption, finally we need a distribution coupling f(v) and v. T (the text on v) and f(N(v)) § Can use Bayes classifier as with ordinary text: estimate a parametric model for the class-conditional joint distribution between the text on the page v and the labels of neighbors of v § Must make naïve Bayes assumptions to keep practical ACFOCS 2004 Chakrabarti 119

Pictorially… § c=class, t=text, N=neighbors § Text-only model: Pr[t|c] § Using neighbors’ text to judge my topic: Pr[t, t(N) | c] (hurts) § Better model: Pr[t, c(N) | c] § Estimate histograms and update based on neighbors’ histograms ACFOCS 2004 Chakrabarti ? 120

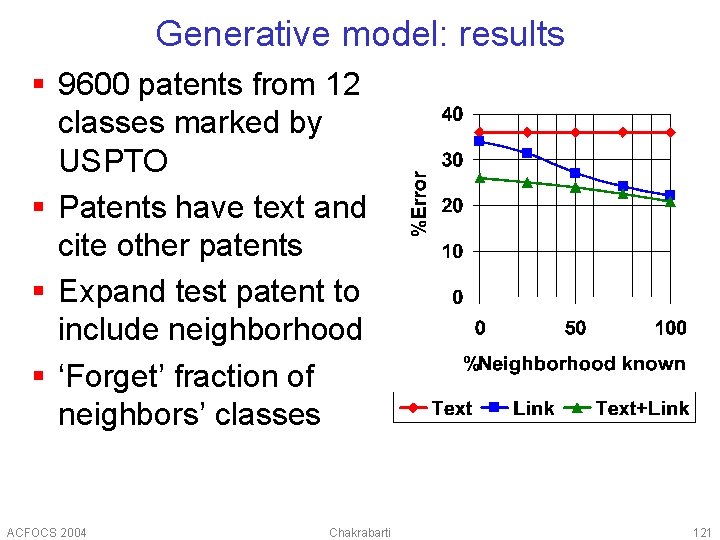
Generative model: results § 9600 patents from 12 classes marked by USPTO § Patents have text and cite other patents § Expand test patent to include neighborhood § ‘Forget’ fraction of neighbors’ classes ACFOCS 2004 Chakrabarti 121

Detour: generative vs. discriminative § x = feature vector, y = label {0, 1} say § Generative method models Pr(x|y) or Pr(x, y) “the generation of data x given label y” § Use Bayes rule to get Pr(y|x) § Inaccurate; x may have many dimensions § Discriminative: directly estimates Pr(y|x) § Simple linear case: want w s. t. w. x > 0 if y=1 and w. x 0 if y=0 § Cannot differentiate for w; instead pick some smooth “loss function” § Works very well in practice ACFOCS 2004 Chakrabarti 122

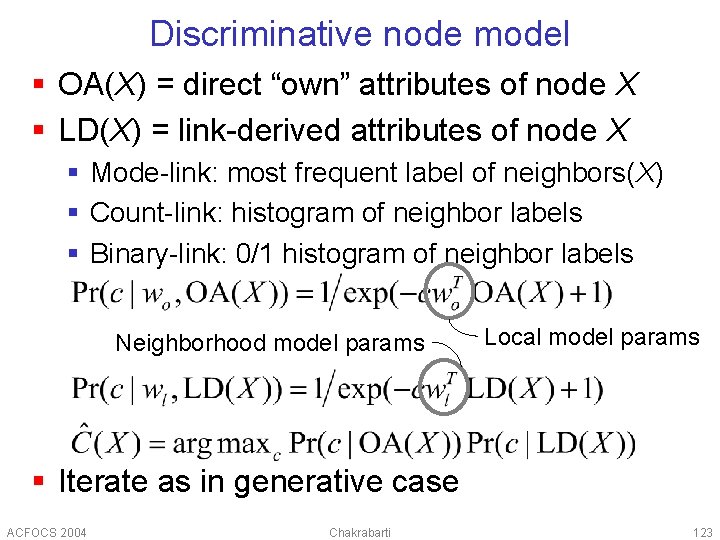
Discriminative node model § OA(X) = direct “own” attributes of node X § LD(X) = link-derived attributes of node X § Mode-link: most frequent label of neighbors(X) § Count-link: histogram of neighbor labels § Binary-link: 0/1 histogram of neighbor labels Neighborhood model params Local model params § Iterate as in generative case ACFOCS 2004 Chakrabarti 123

Discriminative model: results [Li+2003] § Binary-link and count-link outperform content-only at 95% confidence § Better to separately estimate wl and wo § In+Out+Cocitation better than any subset for LD ACFOCS 2004 Chakrabarti 124

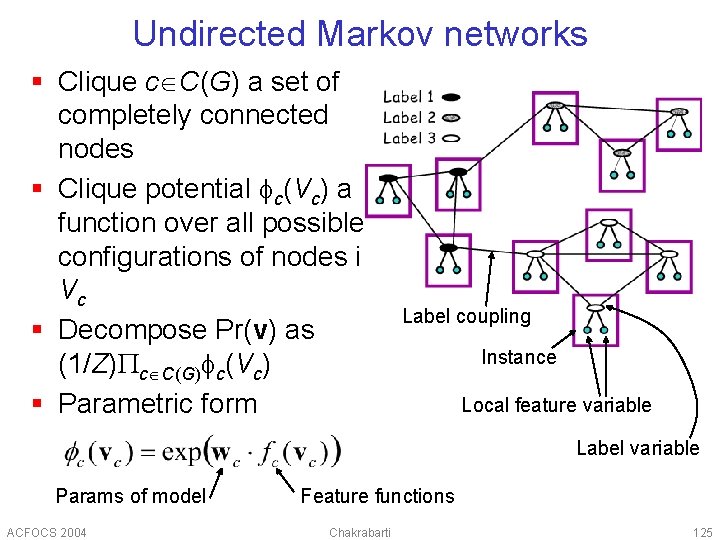
Undirected Markov networks § Clique c C(G) a set of completely connected nodes § Clique potential c(Vc) a function over all possible configurations of nodes in Vc § Decompose Pr(v) as (1/Z) c C(G) c(Vc) § Parametric form Label coupling Instance Local feature variable Label variable Params of model ACFOCS 2004 Feature functions Chakrabarti 125

Conditional and relational networks § x = vector of observed features at all nodes § y = vector of labels § A set of “clique templates” specifying links to use § Other features: “in the same HTML section” ACFOCS 2004 Chakrabarti 126

“Toy problem”: Hierarchical classification § Obvious approaches § Flatten to leaf topics, losing hierarchy info § Level-by-level, compounding error probability § Cascaded generative model r c § Pr(c|d, r) estimated as Pr(c|r)Pr(d|c)/Z(r) § Estimate of Pr(d|c) makes naïve independence assumptions if d has high dimensionality § Pr(c|d, r) tends to 0/1 for large dimensions and § Mistake made at shallow levels become irrevocable ACFOCS 2004 Chakrabarti 127

Global discriminative model § Each node has an associated bit X § Propose a parametric form § Each training instance sets one path to 1, all other nodes have X=0 T d xr=0 xr xr=1 F(d, xr) 2 T+1 wc ACFOCS 2004 Chakrabarti 128

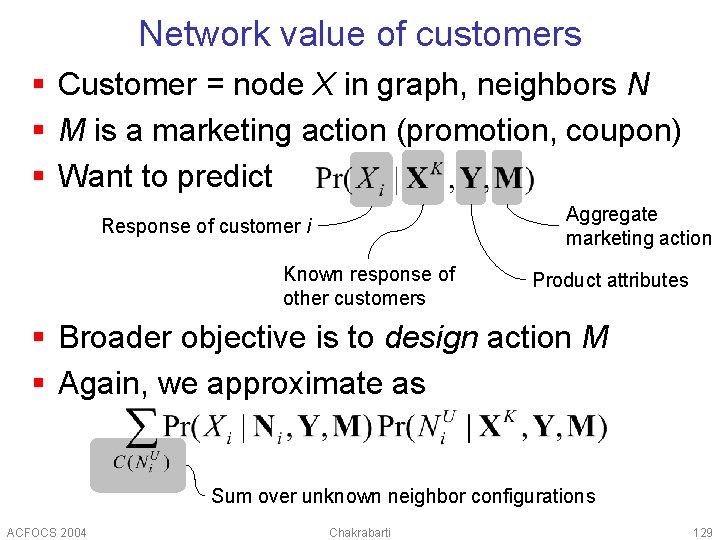
Network value of customers § Customer = node X in graph, neighbors N § M is a marketing action (promotion, coupon) § Want to predict Aggregate marketing action Response of customer i Known response of other customers Product attributes § Broader objective is to design action M § Again, we approximate as Sum over unknown neighbor configurations ACFOCS 2004 Chakrabarti 129

Network value, continued § Let the action be boolean § c is the cost of marketing § r 0 is the revenue without marketing, r 1 with § Expected lift in profit by marketing to customer i in isolation § Global effect ACFOCS 2004 Chakrabarti 130

Special case: sequential networks § Text modeled as sequence of tokens drawn from a large but finite vocabulary § Each token has attributes § Visible: all. Caps, no. Caps, has. Xx, all. Digits, has. Digit, is. Abbrev, (part-of-speech, wn. Sense) § Not visible: part-of-speech, (is. Person. Name, is. Org. Name, is. Location, is. Date. Time), {starts|continues|ends}-noun-phrase § Visible (symbols) and invisible (states) attributes of nearby tokens are dependent § Application decides what is (not) visible § Goal: Estimate invisible attributes ACFOCS 2004 Chakrabarti 131

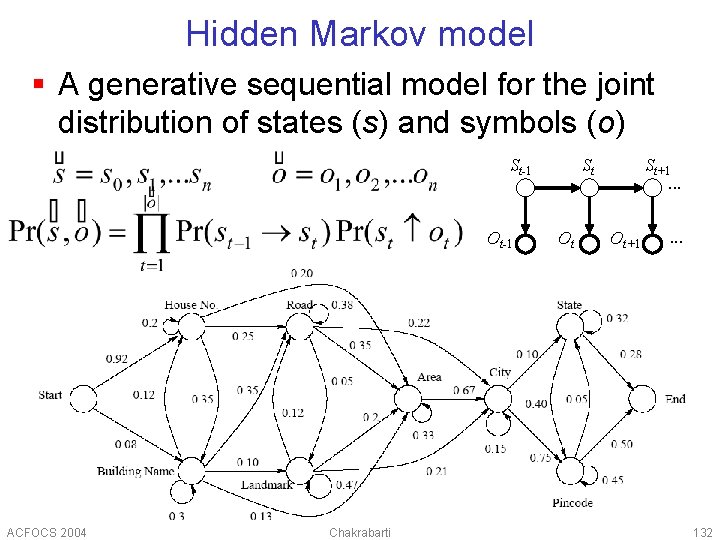
Hidden Markov model § A generative sequential model for the joint distribution of states (s) and symbols (o) St-1 Ot-1 ACFOCS 2004 Chakrabarti St Ot St+1. . . Ot+1 . . . 132

Using redundant token features § Each o is usually a vector of features extracted from a token § Might have high dependence/redundancy: has. Cap, has. Digit, is. Noun, is. Preposition § Parametric model for Pr(st ot) needs to make naïve assumptions to be practical § Overall joint model Pr(s, o) can be very inaccurate § (Same argument as in naïve Bayes vs. SVM or maximum entropy text classifiers) ACFOCS 2004 Chakrabarti 133

Discriminative graphical model § Assume one-stage Markov dependence § Propose direct parametric form for conditional probability of state sequence given symbol sequence St-1 Ot-1 Model St Ot St+1. . . Ot+1 . . . Log-linear form Feature function; might depend on whole o Parameters to fit ACFOCS 2004 Chakrabarti 134

Feature functions and parameters Penalize large params Maximize total conditional likelihood over all instances § Find L/ k for each k and perform a gradient-based numerical optimization § Efficient for linear state dependence structure ACFOCS 2004 Chakrabarti 135

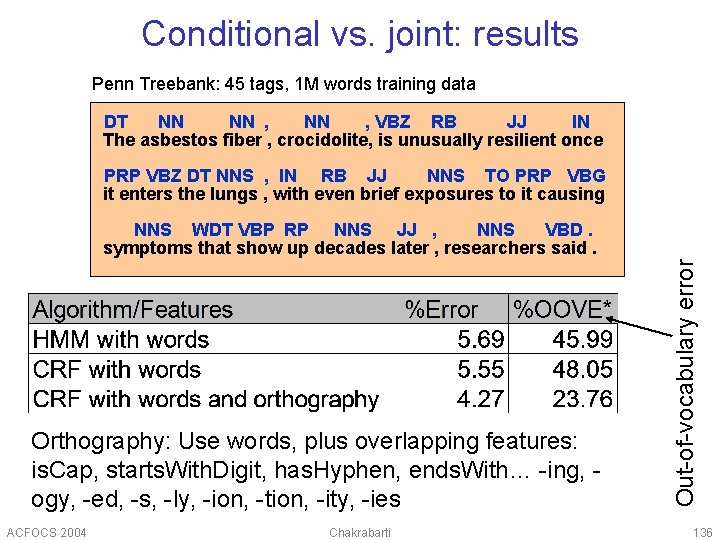
Conditional vs. joint: results Penn Treebank: 45 tags, 1 M words training data DT NN NN , VBZ RB JJ IN The asbestos fiber , crocidolite, is unusually resilient once PRP VBZ DT NNS , IN RB JJ NNS TO PRP VBG it enters the lungs , with even brief exposures to it causing Orthography: Use words, plus overlapping features: is. Cap, starts. With. Digit, has. Hyphen, ends. With… -ing, ogy, -ed, -s, -ly, -ion, -tion, -ity, -ies ACFOCS 2004 Chakrabarti Out-of-vocabulary error NNS WDT VBP RP NNS JJ , NNS VBD. symptoms that show up decades later , researchers said. 136

Summary § Graphs provide a powerful way to model many kinds of data, at multiple levels § Web pages, XML, relational data, images… § Words, senses, phrases, parse trees… § A few broad paradigms for analysis § Factors affecting graph evolution over time § Eigen analysis, conductance, random walks § Coupled distributions between node attributes and graph neighborhood § Several new classes of model estimation and inferencing algorithms ACFOCS 2004 Chakrabarti 137

References § [Brin. P 1998] The Anatomy of a Large-Scale Hypertextual Web Search Engine, WWW. § [Goldman. SVG 1998] Proximity search in databases. VLDB, 26— 37. § [Chakrabarti. DI 1998] Enhanced hypertext categorization using hyperlinks. SIGMOD. § [Bikel. SW 1999] An Algorithm that Learns What’s in a Name. Machine Learning Journal. § [Gibson. KR 1999] Clustering categorical data: An approach based on dynamical systems. VLDB. § [Kleinberg 1999] Authoritative sources in a hyperlinked environment. JACM 46. ACFOCS 2004 Chakrabarti 138

References § [Cohn. C 2000] Probabilistically Identifying Authoritative Documents, ICML. § [Lempel. M 2000] The stochastic approach for linkstructure analysis (SALSA) and the TKC effect. Computer Networks 33 (1 -6): 387 -401 § [Richardson. D 2001] The Intelligent Surfer: Probabilistic Combination of Link and Content Information in Page. Rank. NIPS 14 (1441 -1448). § [Lafferty. MP 2001] Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. ICML. § [Borkar. DS 2001] Automatic text segmentation for extracting structured records. SIGMOD. ACFOCS 2004 Chakrabarti 139

References § [Ng. ZJ 2001] Stable algorithms for link analysis. SIGIR. § [Hulgeri+2001] Keyword Search in Databases. IEEE Data Engineering Bulletin 24(3): 22 -32. § [Hristidis+2002] DISCOVER: Keyword Search in Relational Databases. VLDB. § [Agrawal+2002] DBXplorer: A system for keywordbased search over relational databases. ICDE. § [Taskar. AK 2002] Discriminative probabilistic models for relational data. § [Fagin 2002] Combining fuzzy information: an overview. SIGMOD Record 31(2), 109– 118. ACFOCS 2004 Chakrabarti 140

References § [Chakrabarti 2002] Mining the Web: Discovering Knowledge from Hypertext Data § [Tomlin 2003] A New Paradigm for Ranking Pages on the World Wide Web. WWW. § [Haveliwala 2003] Topic-Sensitive Pagerank: A Context-Sensitive Ranking Algorithm for Web Search. IEEE TKDE. § [Lu. G 2003] Link-based Classification. ICML. § [Faloutsos. MT 2004] Connection Subgraphs in Social Networks. SIAM-DM workshop. § [Pan. YFD 2004] GCap: Graph-based Automatic Image Captioning. MDDE/CVPR. ACFOCS 2004 Chakrabarti 141

References § [Balmin+2004] Authority-Based Keyword Queries in Databases using Object. Rank. VLDB. § [Bar. Yossef. BKT 2004] Sic transit gloria telae: Towards an understanding of the Web’s decay. WWW 2004. ACFOCS 2004 Chakrabarti 142