Using Excel to Implement Software Reliability Models Norman

Using Excel to Implement Software Reliability Models • Norman F. Schneidewind • Naval Postgraduate School • 2822 Racoon Trail, • Pebble Beach, California, 93953, USA • Voice: (831) 656 -2719 • Fax: (831) 372 -0445 • nschneid@nps. navy. mil 1

Outline • • • • • Introduction Characteristics of Excel Implementation Combined Software Reliability Tools – Excel Approach Structure of Combined Approach Notation for Prediction Worksheet Equations for Prediction and Comparison Worksheets Example Prediction Worksheet Analysis of Prediction Worksheet Notation for Actual – Prediction Comparisons Worksheet Example Actual – Prediction Comparisons Worksheet Analysis of Comparison Worksheet Cumulative Failure Prediction Plots Validation of Failure Count Predictions Time to Failure Plot Validation of Time to Failure Predictions Conclusions Excel Demo 2

Introduction • CASRE and SMERFS, hereafter referred to as SRT (software reliability tools), were developed prior to the availability of mature spreadsheet programs. – Programs like Excel were not an option, but things have changed. • In Excel, the user can create equations, do data and statistical analysis, make plots, an do programming, using Visual Basic. • In SRT, the programming of the models has been done for the user, but the functionality is fixed until the next revision. 3

Characteristics of Excel Implementation #1 • Advantages: – Almost all practitioners have Excel. A minority of practitioners have SRT. – Easier for practitioners to use than SRT. – Typically, failure data is provided by practitioners in Excel. – Improve technology transfer: • Predictions can be made by the researcher in the spreadsheet and returned to the practitioner in the same spreadsheet. – Formatted Excel data can be imported into Word and Power. Point for creating reports and presentations. 4

Characteristics of Excel Implementation # 2 • Advantages: – User has more control over formatting of data, prediction results, and plots. – A large set of built-in mathematical and statistical functions are available for reliability analysis. • SRT limited to functions like Chi-square. – User can construct his own reliability equations. • SRT equations are fixed, based on the models implemented. – More flexibility in changing term in equations. • Change cell values; copy and paste equations. 5

Characteristics of Excel Implementation # 3 • Disadvantages: – Column and cell orientation of spreadsheets is cumbersome. • It is not a natural mathematical format. • Need to repeat parameter entries for iterations of equations. • Variable names are not case sensitive. • Variable names cannot be the same as column or cell names. – Thus, some variables must renamed to avoid naming conflicts. 6

Characteristics of Excel Implementation # 4 • Disadvantages: – Mathematical library is not as extensive as Fortran and C++ libraries used in SRT. – Does not have sophisticated model evaluation criteria of SRT. • However, error analysis between actuals and predictions (i. e. , validation) can be done in Excel. 7

Combined Software Reliability Tools – Excel Approach • Best approach may be to combine SRT with Excel. • SRT provides model parameter estimation. – Beyond the capabilities of Excel unless programmed in Visual Basic. – Copy and paste parameters from SRT into spreadsheet. • Excel extends capabilities of SRT by allowing user provided equations, statistical analysis, and plots. 8

Structure of Combined Approach • Worksheets: – Definitions: • Notation • Equations – Predictions • Analysis – Actual – Prediction Comparisons • Analysis • Plots • Validation • Examples of this approach follow. 9

Notation for Prediction Worksheet 10

Equations Time to for Prediction Next and Failure(s) Comparison Predicted Worksheets at Time t Remaining Failures Predicted at Time t: r(t) = ( / ) – Xs, t Cumulative Number of Failures Detected at Time T: D(T) = (α/β)[1 – exp (-β ((T –s + 1)))] + Xs-1 Cumulative Number of Failures Detected Over Life of Software TL: D(TL) = / + Xs-1 References: [1, 2, 3]. 11
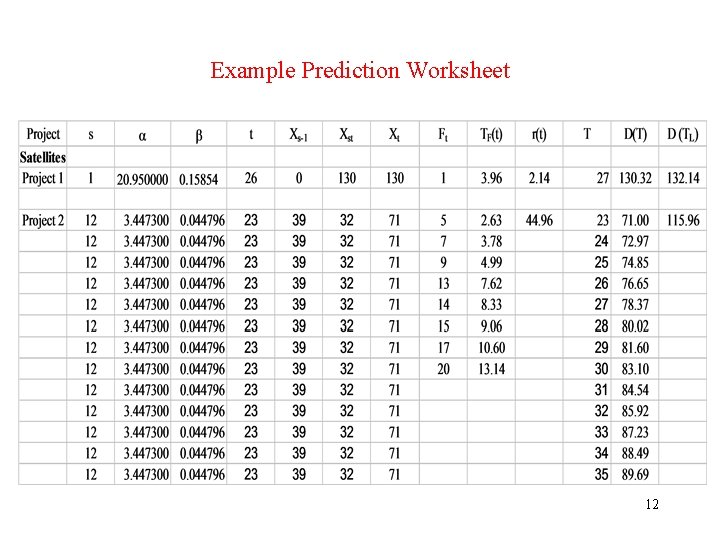
Example Prediction Worksheet 12

Analysis of Prediction Worksheet # 1 • s, , and obtained from SMERFS. • One interval = one week of calendar time. • Project 1: – Optimal s = 1 for both failure count and time to failure predictions. – t=26: interval when time to next failure prediction made This is also the last interval of observed failure data. – X 26 = 130: observed failure count in the range [1, 26]. – F 1 = 1: given number of failures to occur after interval 26. – TF(26) = 3. 96 intervals: time to next failure predicted at time 26 intervals. 13

Analysis of Prediction Worksheet #2 • Project 1: – r(26) = 2. 14: remaining failures predicted at time 26 intervals. – T = 27 intervals: test time. – D(27) = 130. 32: cumulative number of failures detected at time 27 intervals. – D( ) = 132. 14: cumulative number of failures detected over life of software (conservatively, infinity). • r(26) = D( ) - X 26 = 132. 14 – 130 = 2. 14 remaining failures, as in the above. 14

Analysis of Prediction Worksheet #3 • Project 2: – Total range of 35 weeks divided into Parameter Estimation Range = 1, 23 weeks and Prediction Range = 24, 35 weeks for the purpose of model validation. • Model fit using historical data does not demonstrate validity! – Estimate model parameters in range 1, 23 weeks. • Accuracy of future predictions demonstrates validity. – Predict in range 24, 35 weeks and compare with actuals. – Optimal s = 12 for both failure count and time to failure predictions. 15

Analysis of Prediction Worksheet #4 • Project 2: – t=23: interval when time to next failure prediction made – X 11 = 39: observed failure count in the range [1, 11]. – X 12, 23 = 32: observed failure count in the range [12, 23]. – X 23 = 71: observed failure count in the range [1, 23]. – F 1 = 5, …, 20: given number of failures to occur after interval 23. – TF(23) = 2. 63, …, 13. 14 intervals: time to next failures predicted at time 23 intervals. 16

Analysis of Prediction Worksheet #5 • Project 2: – r(23) = 44. 96: remaining failures predicted at time 23 intervals. – T = 23, …, 35 intervals: test time. – D(23, …, 35) = 71. 00, …, 89. 69 cumulative number of failures detected at time 23, …, 35 intervals. – D( ) = 115. 96: cumulative number of failures detected over life of software (conservatively, infinity). • r(23) = D( ) - X 23 = 115. 96 – 71 = 44. 96 remaining failures, as in the above. 17

Notation for Actual – Prediction Comparisons Worksheet • Parameter Estimation Range = 1, 23 weeks; Prediction Range = 24, 35 weeks; s = 12 weeks. • D(T) Actual = Actual Cumulative Count, from Interval 1, in Prediction Range • D(T) Pred = Predicted Cumulative Count, from Interval 1, in Prediction Range • Interval Actual = Difference in D(T) Actual • Interval Pred = Difference in D(T) Pred • Int Act Cum = Interval Actual Cumulative Count, from Interval 24, in Prediction Range • Int Pred Cum = Interval Predicted Cumulative Count, from Interval 24, in Prediction Range • TF(t) Actual = Actual Time to Next Given Number of Failures in the Int Act Cum column • TF(t) Pred = Predicted Time to Next Given Number of Failures in the Int Act Cum column 18
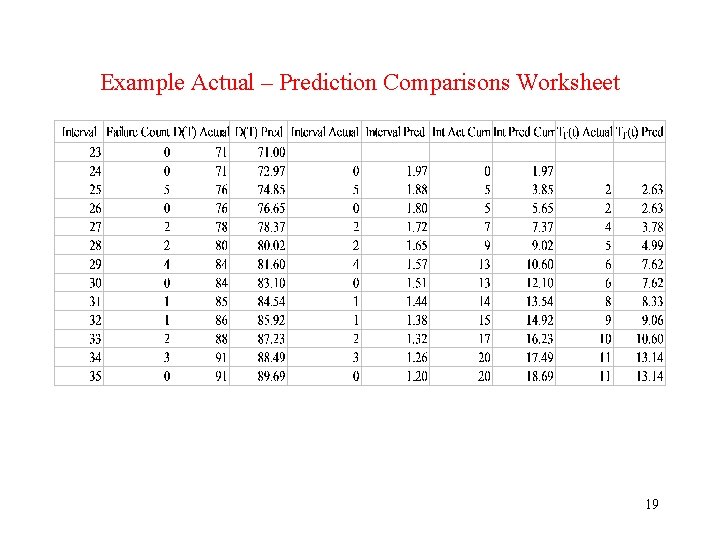
Example Actual – Prediction Comparisons Worksheet 19

Analysis of Comparison Worksheet # 1 • Project 2 – D(T) Actual is compared with D(T) Prediction. • Failure counts are accumulated from Interval 1 in the parameter estimation range, but are compared in the prediction range. – Interval Actual is compared with Interval Prediction. • Interval failure counts are compared in the prediction range. – Int Act Cum is compared with Int Pred Cum. • Interval failure counts are accumulated from Interval 24 in the prediction range and compared in the prediction range. 20

Analysis of Comparison Worksheet # 2 • Project 2 • Make plots in prediction range: – Actual and Predicted Cumulative Failures in Range 1, 35 Weeks. – Actual and Predicted Cumulative Failures in Range 24, 35 Weeks. – Validation of Failure Count Predictions. • Residuals: (Predicted – Actual) versus week. – Residuals do not show bias (i. e. , trend in either positive or negative direction). – Average Residual = -0. 55 failures indicates optimistic prediction on average. 21
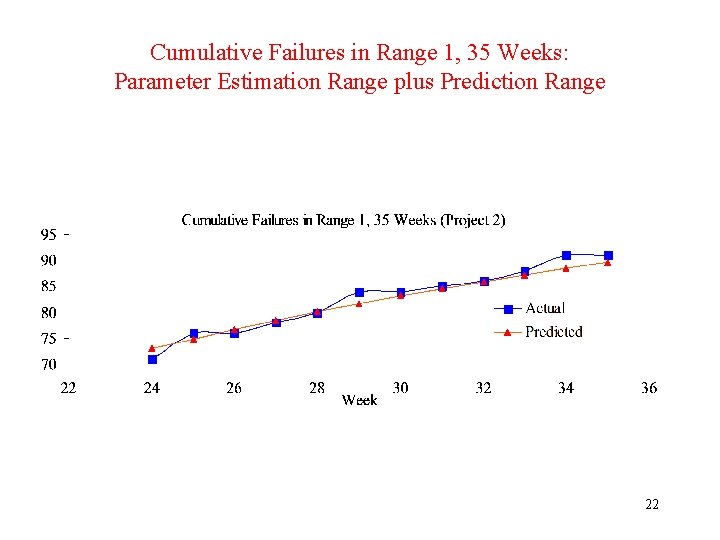
Cumulative Failures in Range 1, 35 Weeks: Parameter Estimation Range plus Prediction Range 22
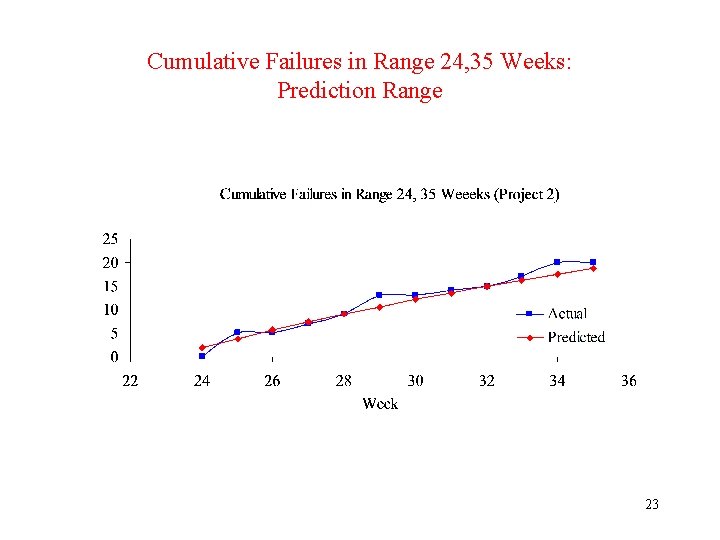
Cumulative Failures in Range 24, 35 Weeks: Prediction Range 23
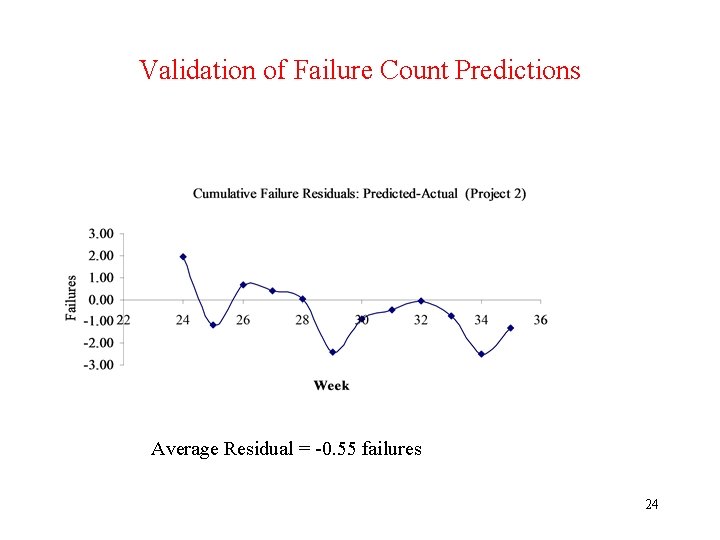
Validation of Failure Count Predictions Average Residual = -0. 55 failures 24

Analysis of Comparison Worksheet # 3 • Project 2 • Make plot in prediction range: – Actual and Predicted Time to Next Failures versus given number of failures. – Validation of Time to Failure Predictions. • Residuals: (Predicted – Actual) versus given number of failures. – Residuals show bias starting at 15 failures (week 32) as it becomes difficult to predict further out into the future. – Average Residual = 0. 87 weeks indicates optimistic prediction on average. 25
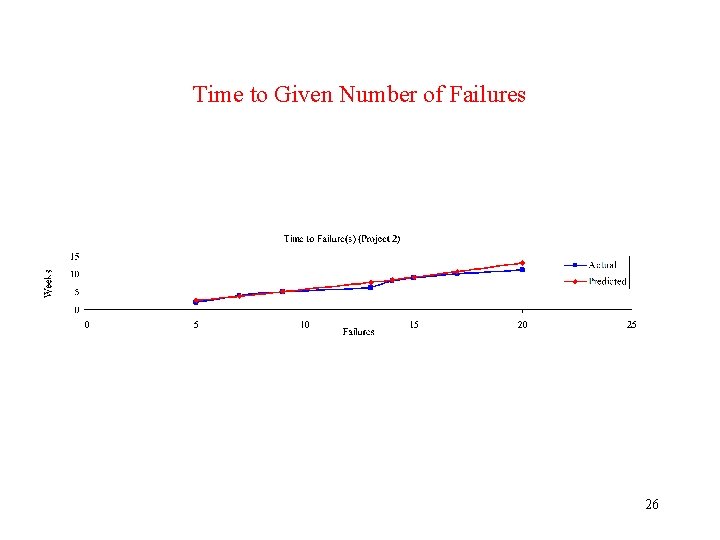
Time to Given Number of Failures 26
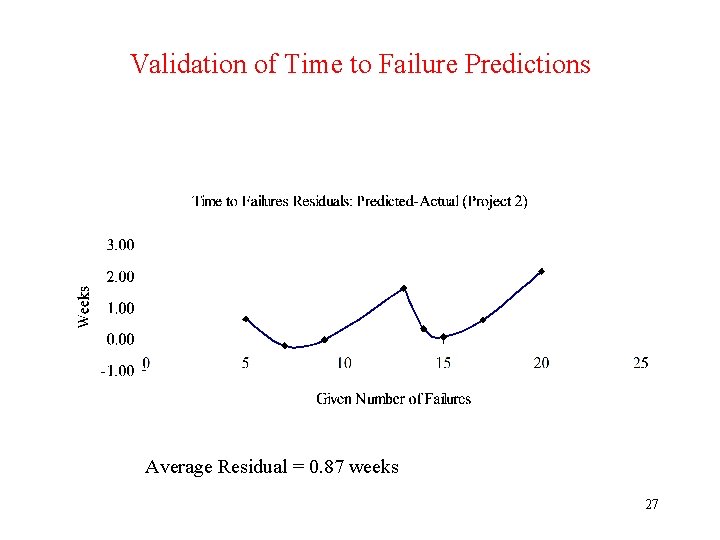
Validation of Time to Failure Predictions Average Residual = 0. 87 weeks 27

Conclusions • Spreadsheet technology can effectively support software reliability modeling and prediction. • Advantages relative to SRT are: – Easier transfer of technology to practitioners. – More user control of program’s operation. – Many built-in mathematical and statistical functions. • Disadvantages relative to SRT are: – Cell format is not conducive to mathematical modeling. – No built-in model evaluation criteria. • SRT and Excel can be combined to advantage: – SRT for reliability model parameter estimation. – Excel for reliability prediction. 28
![References • [1] Norman F. Schneidewind, "Reliability Modeling for Safety Critical Software", IEEE Transactions References • [1] Norman F. Schneidewind, "Reliability Modeling for Safety Critical Software", IEEE Transactions](http://slidetodoc.com/presentation_image_h2/607e17e4230bbd8c5a104f6405f5ea57/image-29.jpg)
References • [1] Norman F. Schneidewind, "Reliability Modeling for Safety Critical Software", IEEE Transactions on Reliability, Vol. 46, No. 1, March 1997, pp. 88 -98. • [2] Norman F. Schneidewind, "Software Reliability Model with Optimal Selection of Failure Data", IEEE Transactions on Software Engineering, Vol. 19, No. 11, November 1993, pp. 1095 -1104. • [3] Norman F. Schneidewind and T. W. Keller, "Application of Reliability Models to the Space Shuttle", IEEE Software, Vol. 9, No. 4, July 1992 pp. 28 -33. 29
- Slides: 29