Using Congruent Triangles Ch 4 Lesson 5 CPCTC


- Slides: 28

Using Congruent Triangles Ch 4 Lesson 5

CPCTC • Corresponding parts of congruent triangles are congruent (CPCTC): Once two triangles are proven to be congruent than all corresponding parts of the two triangles are congruent

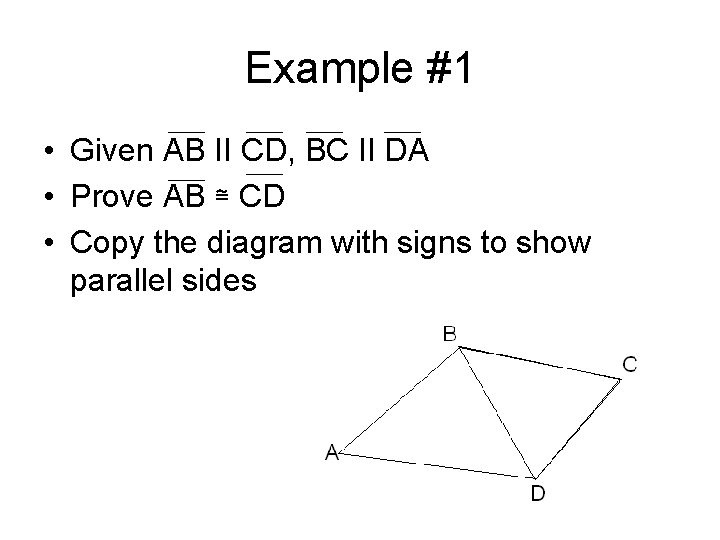
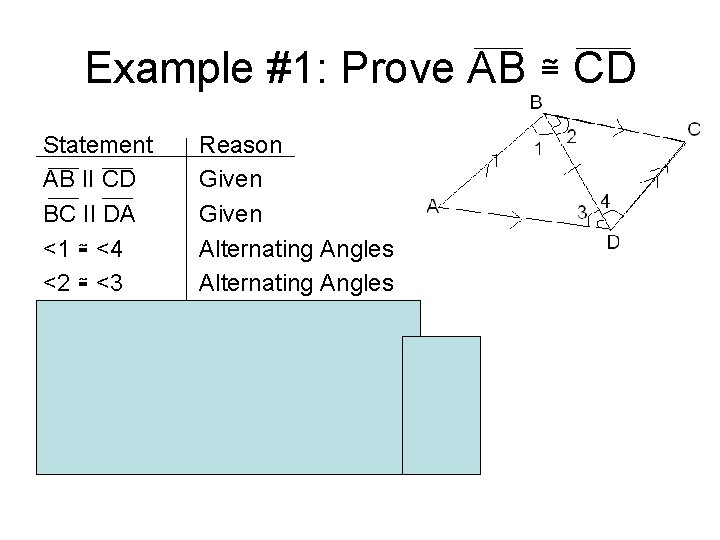
Example #1 • Given AB II CD, BC II DA • Prove AB ≅ CD • Copy the diagram with signs to show parallel sides

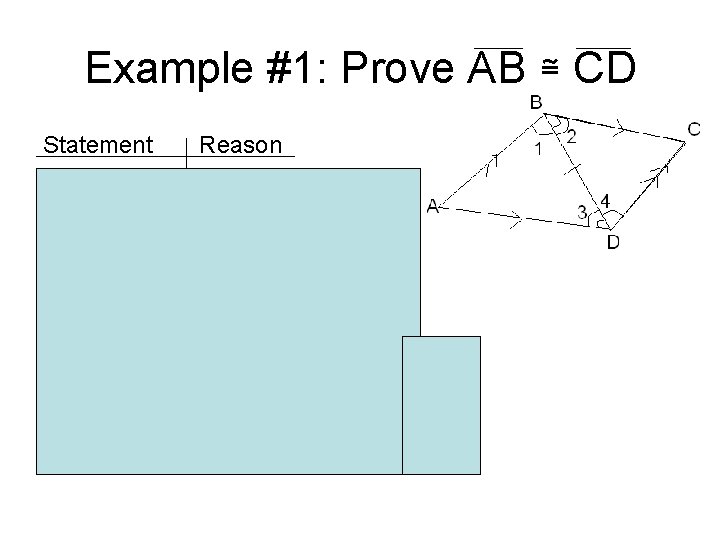
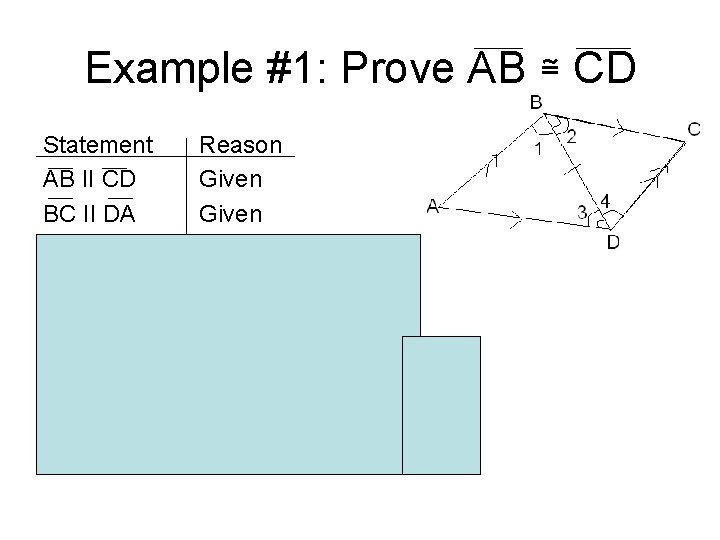
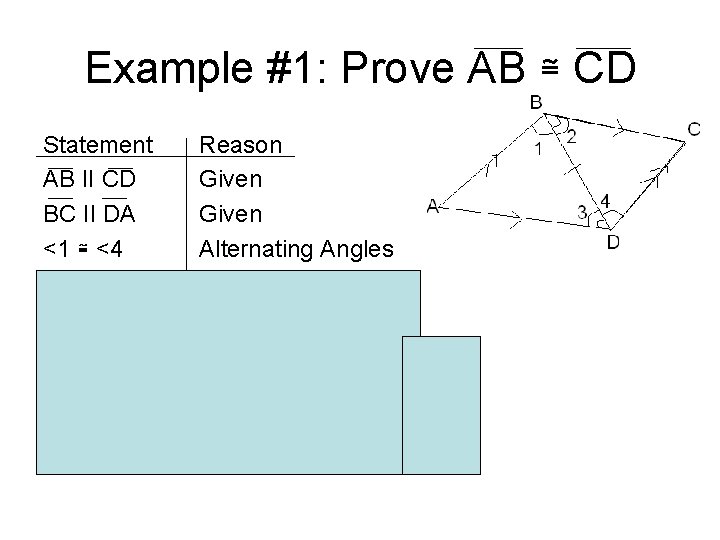
Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ABC ≅ BDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) Corresponding Sides of congruent triangles are congruent

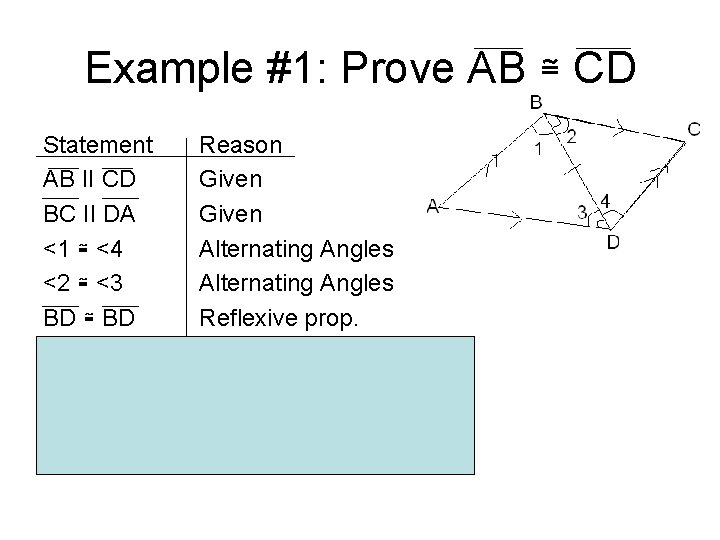
Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ABC ≅ BDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) Corresponding Sides of congruent triangles are congruent

Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ABC ≅ BDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) Corresponding Sides of congruent triangles are congruent

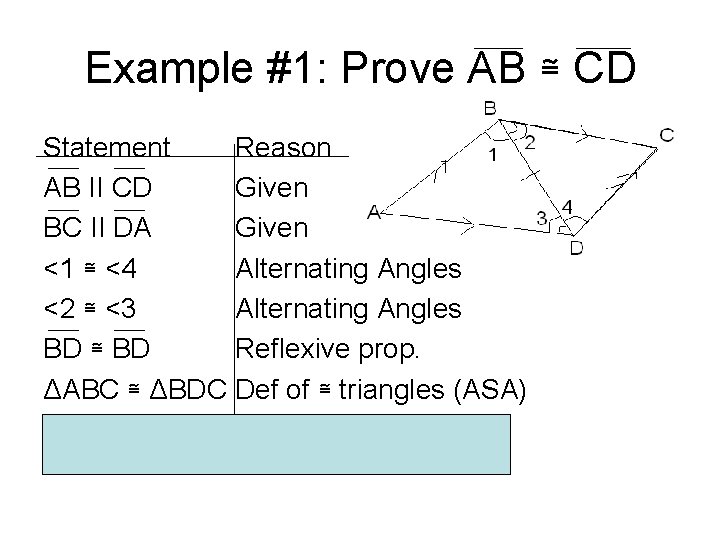
Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ABC ≅ BDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) Corresponding Sides of congruent triangles are congruent

Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ABC ≅ BDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) Corresponding Sides of congruent triangles are congruent

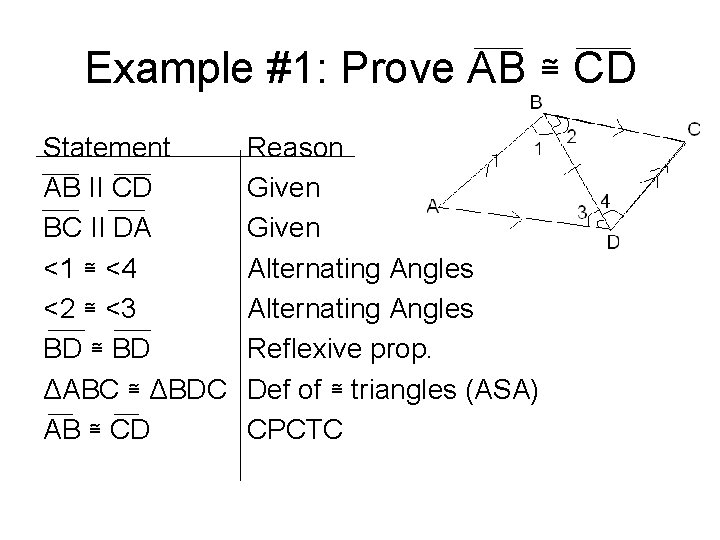
Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ΔABC ≅ ΔBDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) CPCTC

Example #1: Prove AB ≅ CD Statement AB II CD BC II DA <1 ≅ <4 <2 ≅ <3 BD ≅ BD ΔABC ≅ ΔBDC AB ≅ CD Reason Given Alternating Angles Reflexive prop. Def of ≅ triangles (ASA) CPCTC

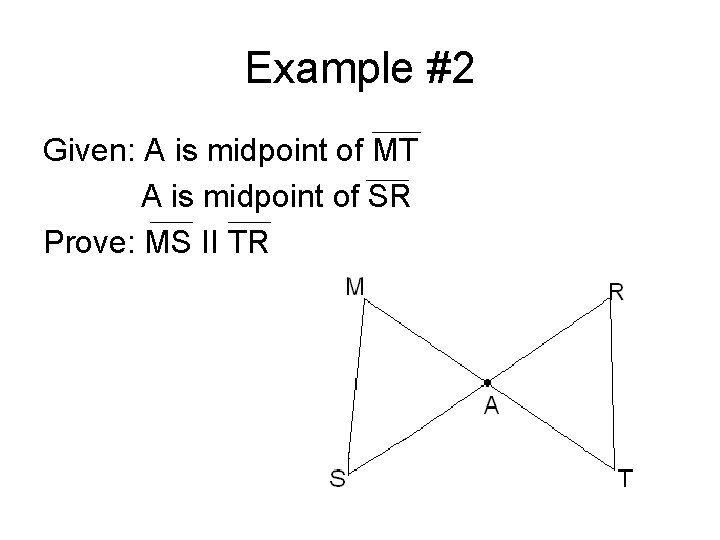
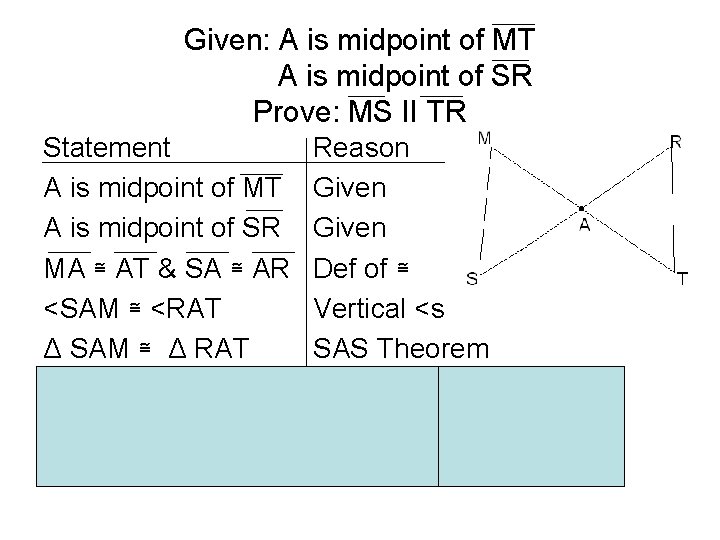
Example #2 Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR

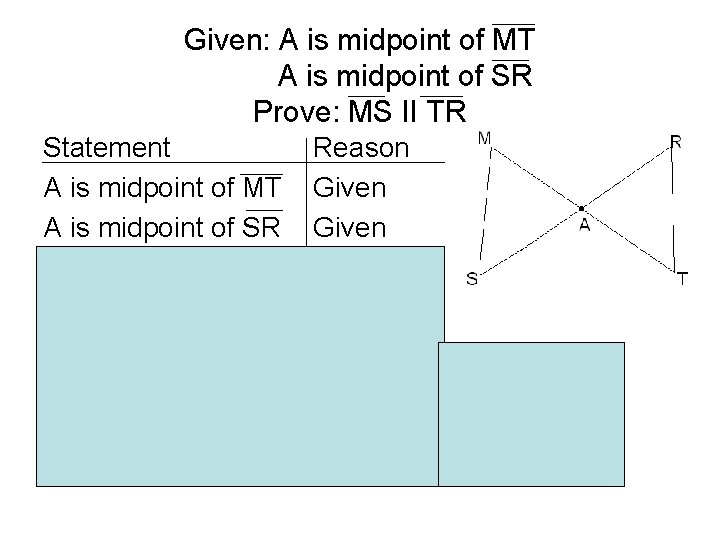
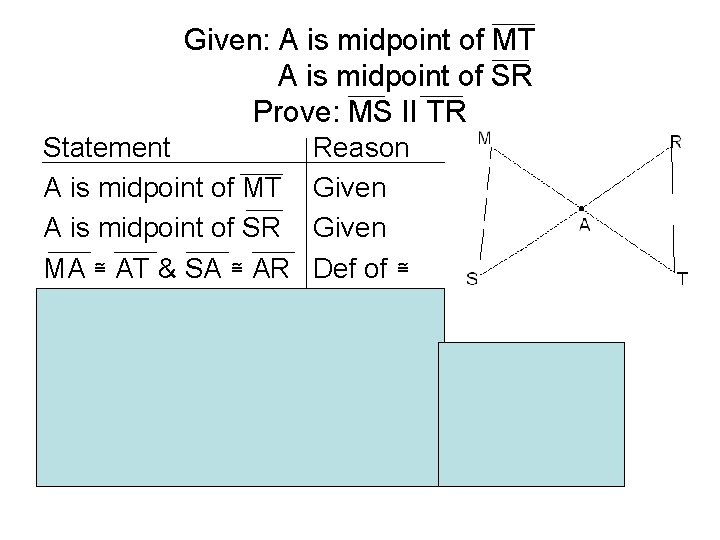
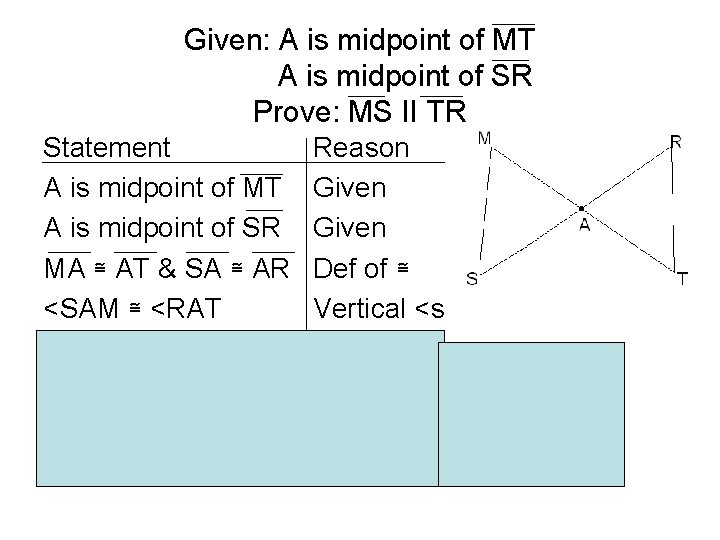
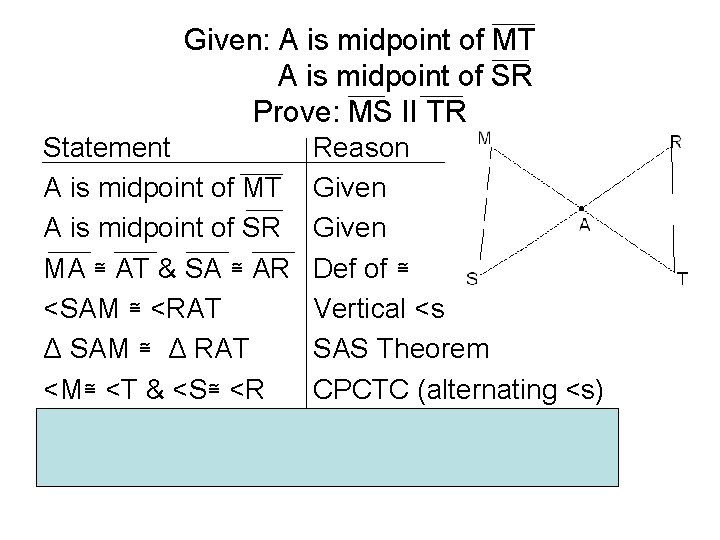
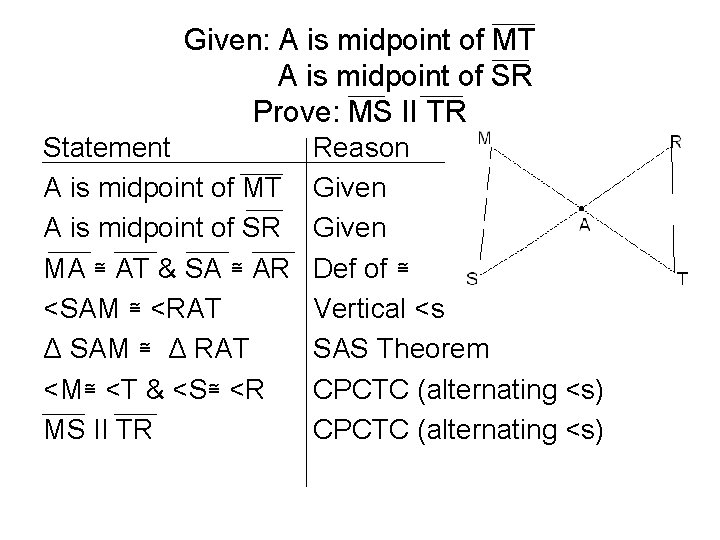
Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

Given: A is midpoint of MT A is midpoint of SR Prove: MS II TR Statement A is midpoint of MT A is midpoint of SR MA ≅ AT & SA ≅ AR <SAM ≅ <RAT Δ SAM ≅ Δ RAT <M≅ <T & <S≅ <R MS II TR Reason Given Def of ≅ Vertical <s SAS Theorem CPCTC (alternating <s)

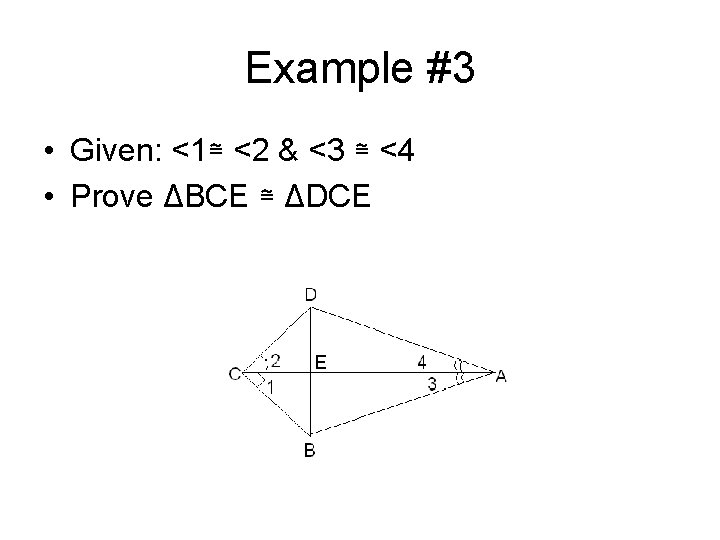
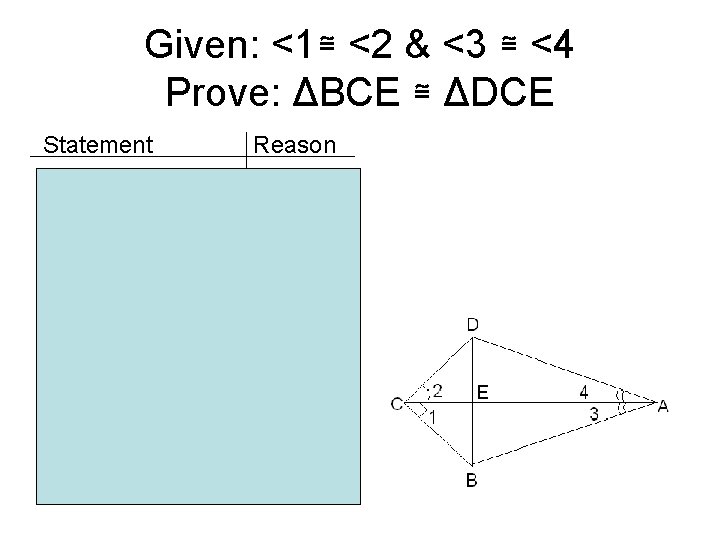
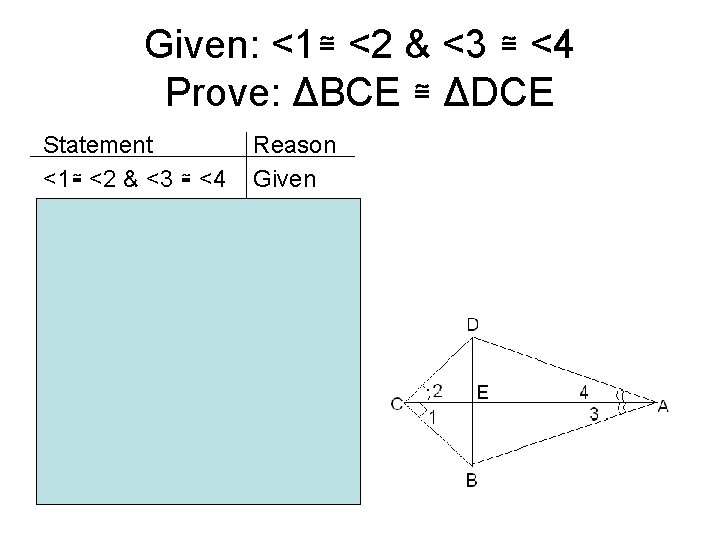
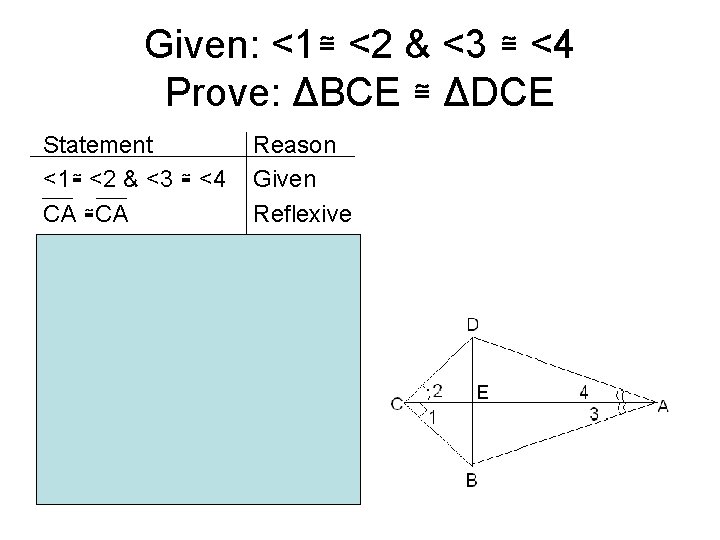
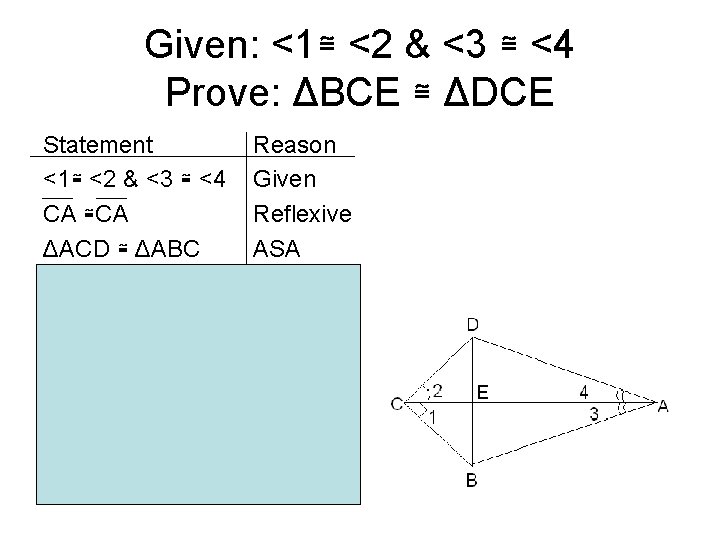
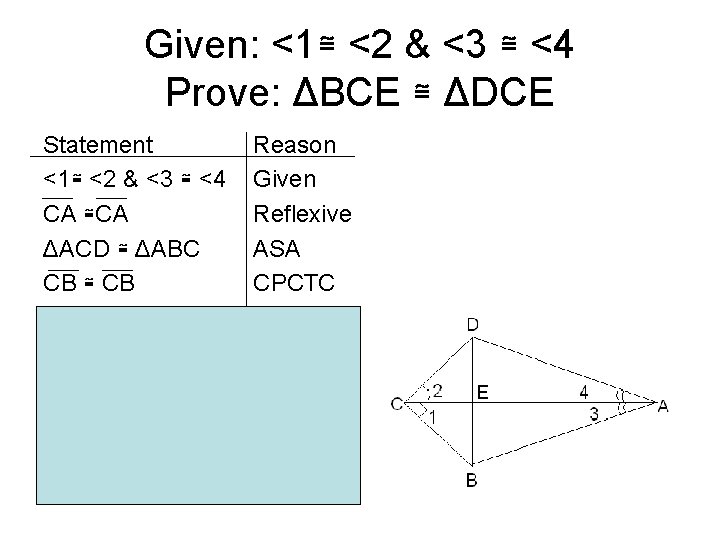
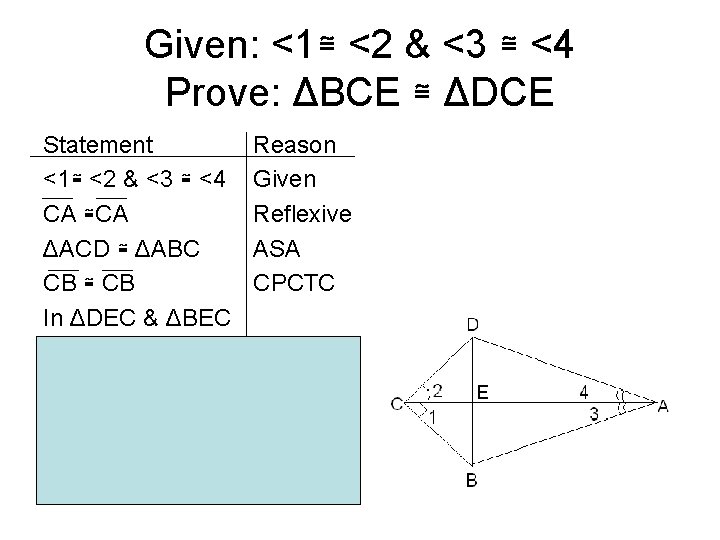
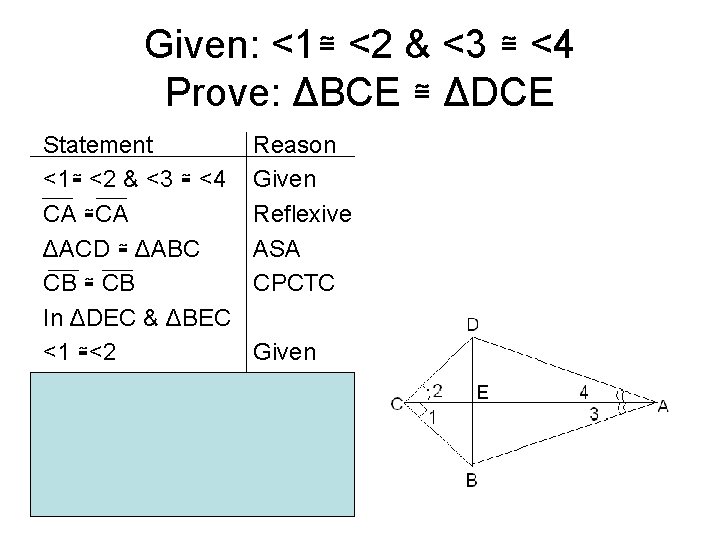
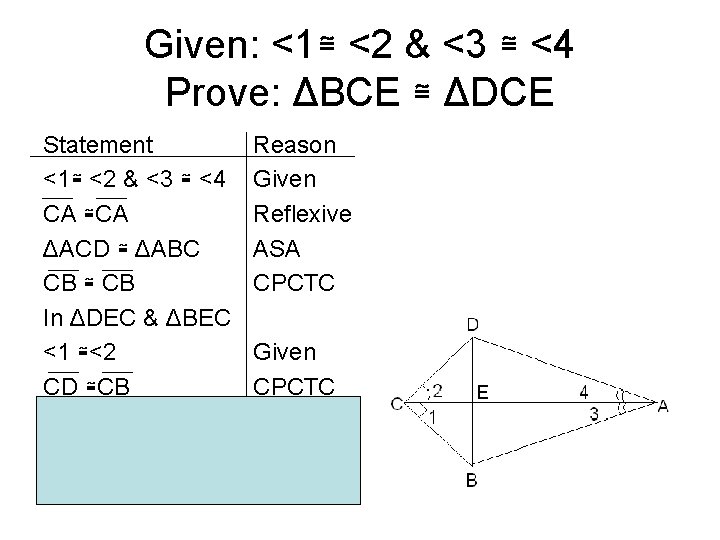
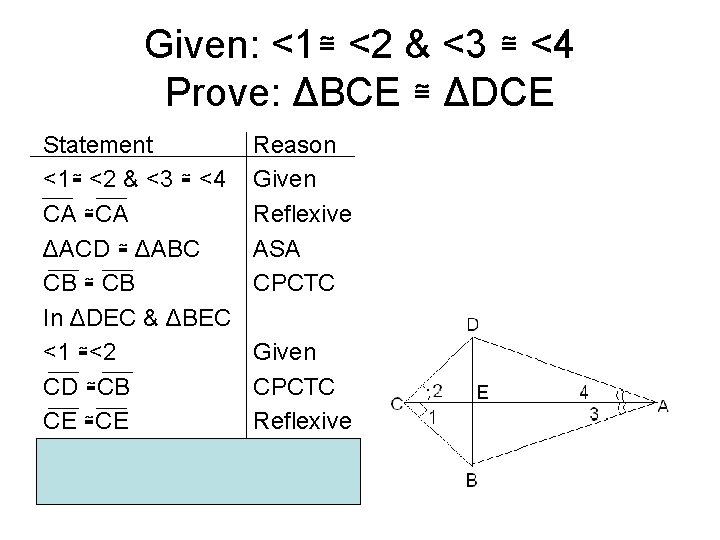
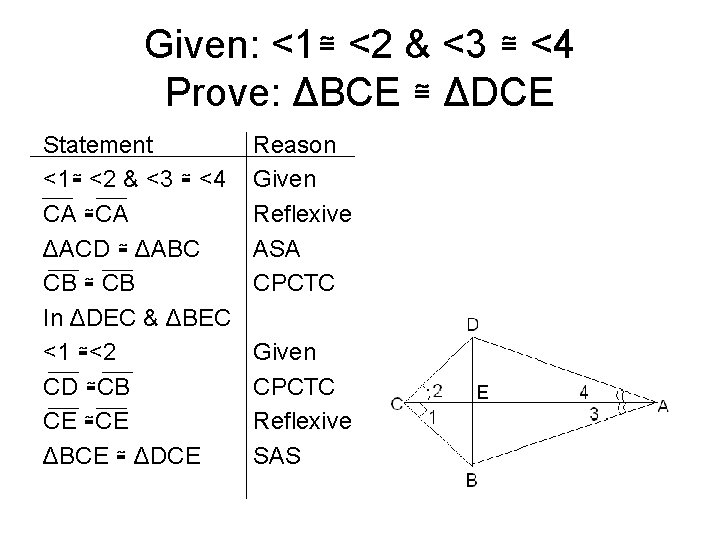
Example #3 • Given: <1≅ <2 & <3 ≅ <4 • Prove ΔBCE ≅ ΔDCE

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS

Given: <1≅ <2 & <3 ≅ <4 Prove: ΔBCE ≅ ΔDCE Statement <1≅ <2 & <3 ≅ <4 CA ≅CA ΔACD ≅ ΔABC CB ≅ CB In ΔDEC & ΔBEC <1 ≅<2 CD ≅CB CE ≅CE ΔBCE ≅ ΔDCE Reason Given Reflexive ASA CPCTC Given CPCTC Reflexive SAS