Using CGH for Testing Aspheric Surfaces Nasrin Ghanbari

Using CGH for Testing Aspheric Surfaces Nasrin Ghanbari OPTI 521

Introduction �Spherical wavefront from interferometer is incident on CGH �Reflected light will have an aspheric phase function �CGH cancels the aspheric phase �Emerging wavefront will be spherical and it goes back to interferometer Aspheric Mirror CGH

Design Process Design of CGH in Zemax Conversion to line pattern Fabrication Alignment CGH �Start with design and optimization of CGH in Zemax: �Single pass geometry �Phase function �Double pass geometry

Virtual Glass �Snell’s law: �If n 1 = 0 then sin θ 2 =0 �Therefore θ 2 =0 and the emerging ray is perpendicular to aspheric surface

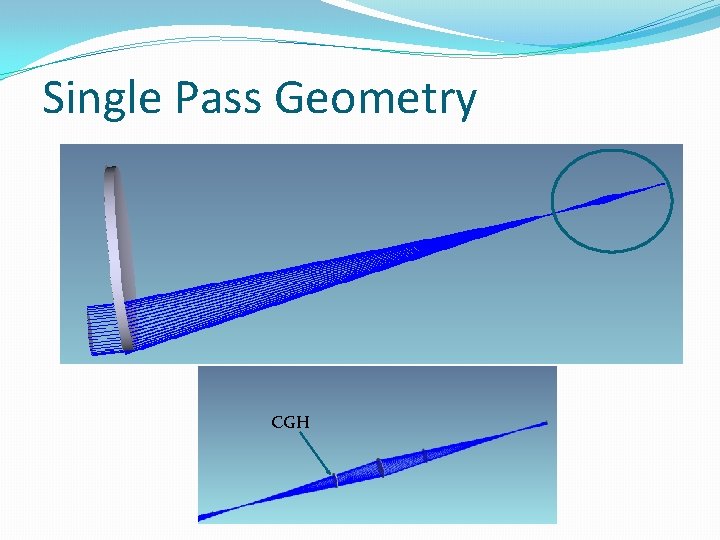
Single Pass Geometry CGH

Beam Footprint �Width of the spot size: �The number of waves of tilt needed to separate diffraction orders: [1] Dr. Jim Burge, “Computer Generated Holograms for Optical Testing”

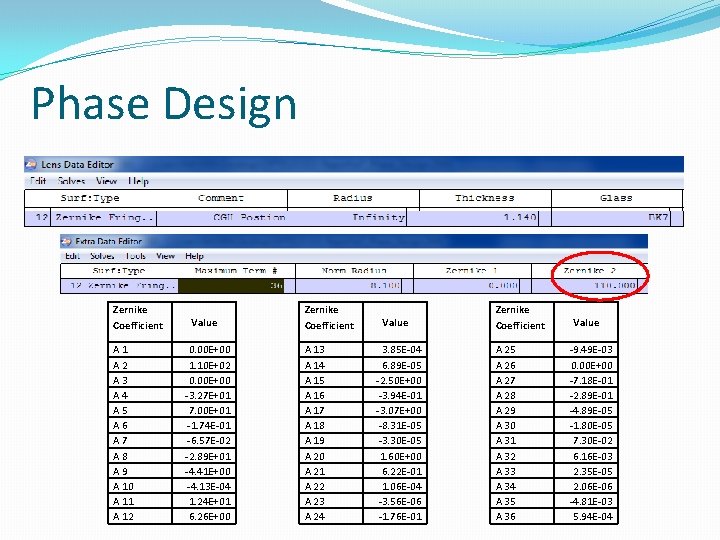
Phase Design Zernike Coefficient A 1 A 2 A 3 A 4 A 5 A 6 A 7 A 8 A 9 A 10 A 11 A 12 Value 0. 00 E+00 1. 10 E+02 0. 00 E+00 -3. 27 E+01 7. 00 E+01 -1. 74 E-01 -6. 57 E-02 -2. 89 E+01 -4. 41 E+00 -4. 13 E-04 1. 24 E+01 6. 26 E+00 Zernike Coefficient A 13 A 14 A 15 A 16 A 17 A 18 A 19 A 20 A 21 A 22 A 23 A 24 Value 3. 85 E-04 6. 89 E-05 -2. 50 E+00 -3. 94 E-01 -3. 07 E+00 -8. 31 E-05 -3. 30 E-05 1. 60 E+00 6. 22 E-01 1. 06 E-04 -3. 56 E-06 -1. 76 E-01 Zernike Coefficient A 25 A 26 A 27 A 28 A 29 A 30 A 31 A 32 A 33 A 34 A 35 A 36 Value -9. 49 E-03 0. 00 E+00 -7. 18 E-01 -2. 89 E-01 -4. 89 E-05 -1. 80 E-05 7. 30 E-02 6. 16 E-03 2. 35 E-05 2. 06 E-06 -4. 81 E-03 5. 94 E-04

Zernike Fringe Phase Ai Zi (ρ, φ) A 1 1 A 2 ρ cos(φ) A 3 ρ sin(φ) A 4 2 ρ2 - 1 A 5 ρ2 cos (2 φ) A 6 ρ2 sin(2 φ). . . �M is the diffraction order of the CGH �N is the number of Zernike terms; Zemax supports up to 37 �Zi (ρ, φ) is the ith term in the Zernike polynomial �Ai is the coefficient of that term in units of waves.

Double Pass Geometry �The double pass geometry models the physical setup. �Check the separation of various diffraction orders �Flip the sign of diffraction order for CGH and radius of curvature for the mirror

Diffraction Orders �Use multi-configuration editor in Zemax �The +1 diffraction order appears in red �To block other orders place an aperture at best focus.

Sources of Error �Pattern Distortion: error in the positioning of the fringe lines �Misalignment of CGH: alignment marks and cross hairs are placed around the main CGH [2] R. Zehnder, J. Burge and C. Zhao, “Use of computer generated holograms for alignment of complex null correctors”

2 D Line Pattern Phase Function Wavefront Profile [1] Spacing Chrome Segment Position on Substrate [1] Dr. Jim Burge, “Computer Generated Holograms for Optical Testing”

Physical Setup CGH *Photos taken at the Mirror Lab

Conclusion �Phase function of CGH can be optimized for a particular testing geometry. �The process is carried out in three steps �Tilt must be added to CGH to separate +1 order from the other diffraction orders. �Diffraction efficiency was not discussed; for an amplitude grating it is about 10% for the +1 order �For accurate placement of CGH in the testing setup, it is necessary to include the alignment CGH.

Thank You �Chunyu Zhao �Daewook Kim �Javier Del Hoyo �Todd Horne �Wenrui Cai �Won Hyun Park