Using Bitboards for Move Generation in Shogi Reijer

Using Bitboards for Move Generation in Shogi Reijer Grimbergen Department of Informatics Yamagata University 2006/11/11 GPW 2006 1

Outline Why this presentation? Basic bitboards Attack bitboards Other bitboards Experimental results Conclusions and future work 2006/11/11 GPW 2006 2

Why this presentation? Bitboards are not a new idea Have been used in chess for a long time Bitboards are not new in shogi Yamashita has explained how to use bitboards in shogi Bonanza uses bitboards Why then this presentation? Yamashita’s explanation is buried in his BBS There are some details that can be optimized I don’t agree with Yamashita’s conclusion No concise explanation about bitboards 2006/11/11 GPW 2006 3

Basic bitboards What are bitboards? Bitboards are a binary representation of knowledge for all squares on the board Presence of knowledge is represented by setting the bit for the square to 1 Absence of knowledge is represented by setting the bit for the square to 0 Chess programs use bitboards for expressing many different types of knowledge 2006/11/11 GPW 2006 4

Basic bitboards Bitboards in chess One bitboard can be represented with a 64 bit integer Yamashita’s representation Represent a bitboard with three integers Hoki’s optimization Represent a bitboard with an array of three integers typedef struct { unsigned int bb[3]; } BITBOARD; 2006/11/11 GPW 2006 5
![9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26 9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26](http://slidetodoc.com/presentation_image_h/802b8090b3e9162d6f61ee1147e77746/image-6.jpg)
9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 GPW 2006 a b c d e f g h i 6

Basic bitboards Logical operations on bitboards void And. BB(BITBOARD *to, *from 1, *from 2) { to→bb[0] = from 1→bb[0] & from 2→bb[0]; to→bb[1] = from 1→bb[1] & from 2→bb[1]; to→bb[2] = from 1→bb[2] & from 2→bb[2]; } Similar operations for OR, XOR and NOT Other basic operations on bitboards Clear. BB: setting all bits to 0 Set. BB: setting all bits to 1 Copy. BB: copying a bitboard 2006/11/11 GPW 2006 7
![Basic bitboards 9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] Basic bitboards 9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2]](http://slidetodoc.com/presentation_image_h/802b8090b3e9162d6f61ee1147e77746/image-8.jpg)
Basic bitboards 9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 GPW 2006 1 1 1 1 1 a 0 1 0 0 0 1 0 b 1 1 1 1 1 c 0 0 0 0 0 d 0 0 0 0 0 e 0 0 0 0 0 f 1 1 1 1 1 g 0 1 0 0 0 1 0 h 1 1 1 1 1 i 8

Basic bitboards Bitboards for position information Occupied: bitboard for the occupied squares Sente. Pieces: bitboard for the black pieces Gote. Pieces: bitboard for the white pieces Bitboards for each type of piece for black and white • Sente. Gold: has 1 s for the squares with black golds The bitboards with position information must be updated at every move 2006/11/11 GPW 2006 9

Attack bitboards Non-sliding pieces 81 bitboards for each piece Example: bitboard for black gold on 5 e 2006/11/11 9 8 7 6 5 4 3 2 1 0 0 0 0 0 a 0 0 0 0 0 b 0 0 0 0 0 c 0 0 0 1 1 1 0 0 0 d 0 0 0 1 0 0 0 e 0 0 1 0 0 f 0 0 0 0 0 g 0 0 0 0 0 h 0 0 0 0 0 i GPW 2006 10

Attack bitboards Horizontal attacks Pre-calculate bitboards for all possible blocking possibilities Example Block pattern of the rook on 7 h (square 66): 001010110 = 86 bb[2] = 00000110110000000 = 221184 Rank. Attacks[66][86]. bb[2] : = 221184 g 飛 香桂 2006/11/11 金 h 銀玉 金 桂香 GPW 2006 i 11
![Attack bitboards Problem BITBOARD Rank. Attacks[81][512] is a big piece of memory (497 Kb) Attack bitboards Problem BITBOARD Rank. Attacks[81][512] is a big piece of memory (497 Kb)](http://slidetodoc.com/presentation_image_h/802b8090b3e9162d6f61ee1147e77746/image-12.jpg)
Attack bitboards Problem BITBOARD Rank. Attacks[81][512] is a big piece of memory (497 Kb) Optimization (Hyatt) Edge squares do not change the piece attack BITBOARD Rank. Attacks[81][128] (124 Kb) g 歩飛 金 銀玉 香桂 2006/11/11 金 桂香 h i GPW 2006 12

Attack bitboards Vertical attacks For horizontal attacks the bits are in consecutive positions, so masking and shifting is enough For vertical attacks the bits are 9 positions apart Solution (Hyatt) Rotate the board 90 degrees Needs a new bitboard Occupied_rot 90 that has to be updated at every move Can be used for both rooks and lances in shogi 2006/11/11 GPW 2006 13
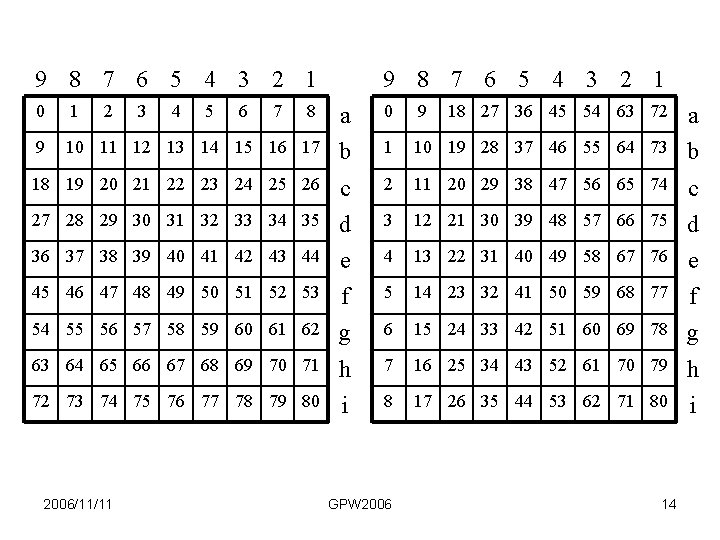
9 8 7 6 5 4 3 2 1 2 0 1 8 a 0 9 18 27 36 45 54 63 72 a 9 10 11 12 13 14 15 16 17 b 1 10 19 28 37 46 55 64 73 b 18 19 20 21 22 23 24 25 26 c 2 11 20 29 38 47 56 65 74 c 27 28 29 30 31 32 33 34 35 d 3 12 21 30 39 48 57 66 75 d 36 37 38 39 40 41 42 43 44 e 4 13 22 31 40 49 58 67 76 e 45 46 47 48 49 50 51 52 53 f 5 14 23 32 41 50 59 68 77 f 54 55 56 57 58 59 60 61 62 g 6 15 24 33 42 51 60 69 78 g 63 64 65 66 67 68 69 70 71 h 7 16 25 34 43 52 61 70 79 h 72 73 74 75 76 77 78 79 80 i 8 17 26 35 44 53 62 71 80 i 2006/11/11 3 4 5 6 7 9 8 7 6 5 4 3 2 1 GPW 2006 14
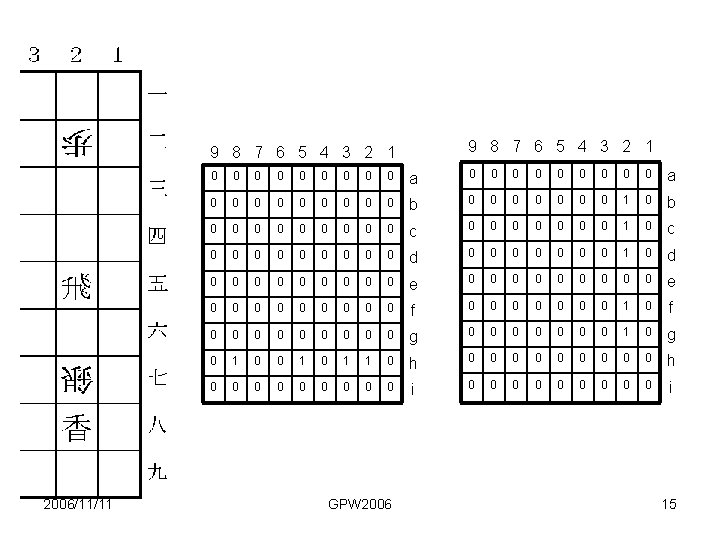
9 8 7 6 5 4 3 2 1 2006/11/11 0 0 0 0 0 a 0 0 0 0 0 b 0 0 0 0 1 0 b 0 0 0 0 0 c 0 0 0 0 1 0 c 0 0 0 0 0 d 0 0 0 0 1 0 d 0 0 0 0 0 e 0 0 0 0 0 f 0 0 0 0 1 0 f 0 0 0 0 0 g 0 0 0 0 1 0 g 0 1 0 1 1 0 h 0 0 0 0 0 i 0 0 0 0 0 i GPW 2006 15

Attack bitboards Diagonal attacks For bishops the bits along a diagonal are not adjacent Solution (Hyatt) Use rotations of 45 degrees clockwise and 45 degrees anti-clockwise Needs new bitboards Occupied_r 45 and Occupied_l 45 which must be updated at every move 2006/11/11 GPW 2006 16

0 9 8 18 1 27 10 2 19 36 7 28 11 6 3 20 12 13 5 54 6 14 46 14 55 30 47 22 39 7 56 8 73 34 38 65 75 32 49 17 66 2006/11/11 40 57 25 74 26 31 48 41 58 67 50 59 25 13 24 35 23 34 33 44 43 53 42 51 12 22 32 42 52 62 1 15 64 16 33 21 2 63 23 72 24 29 26 15 4 3 37 16 5 4 45 17 11 21 31 41 51 61 71 0 10 20 30 40 50 60 70 80 9 19 29 39 49 59 69 79 18 28 38 48 58 68 78 27 37 47 57 67 GPW 2006 17 77
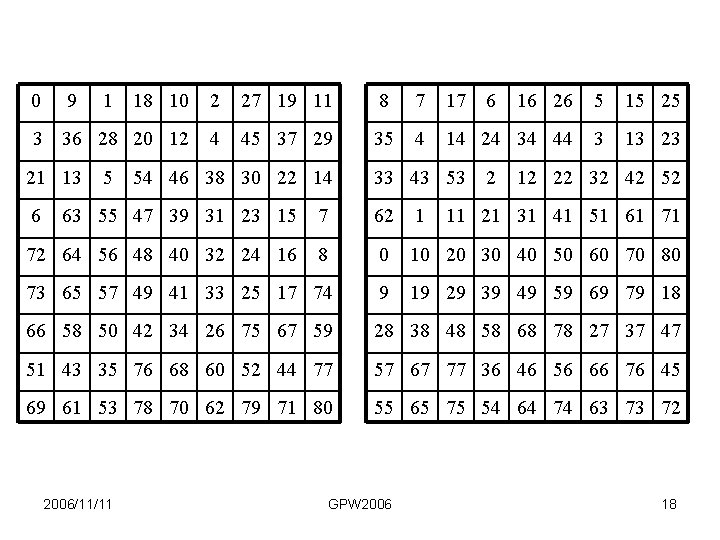
0 9 18 10 2 27 19 11 8 7 17 16 26 5 15 25 3 36 28 20 12 4 45 37 29 35 4 14 24 34 44 3 13 23 21 13 6 1 5 54 46 38 30 22 14 33 43 53 6 2 12 22 32 42 52 63 55 47 39 31 23 15 7 62 1 72 64 56 48 40 32 24 16 8 0 10 20 30 40 50 60 70 80 73 65 57 49 41 33 25 17 74 9 19 29 39 49 59 69 79 18 66 58 50 42 34 26 75 67 59 28 38 48 58 68 78 27 37 47 51 43 35 76 68 60 52 44 77 57 67 77 36 46 56 66 76 45 69 61 53 78 70 62 79 71 80 55 65 75 54 64 74 63 73 72 2006/11/11 GPW 2006 11 21 31 41 51 61 71 18
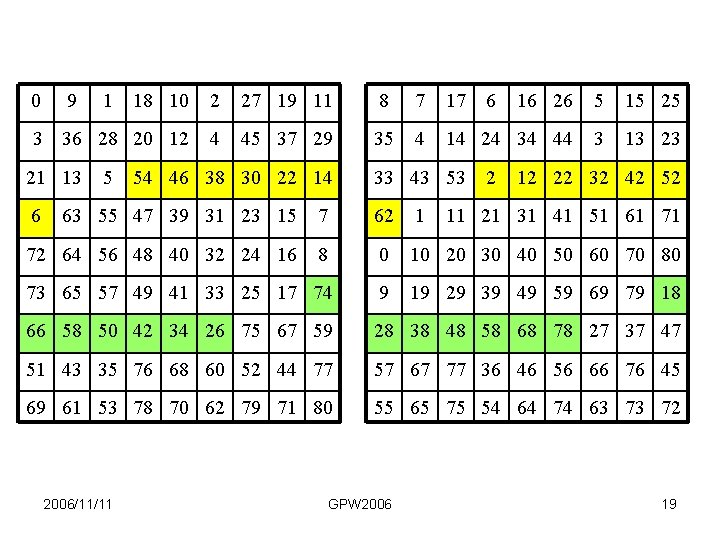
0 9 18 10 2 27 19 11 8 7 17 16 26 5 15 25 3 36 28 20 12 4 45 37 29 35 4 14 24 34 44 3 13 23 21 13 6 1 5 54 46 38 30 22 14 33 43 53 6 2 12 22 32 42 52 63 55 47 39 31 23 15 7 62 1 72 64 56 48 40 32 24 16 8 0 10 20 30 40 50 60 70 80 73 65 57 49 41 33 25 17 74 9 19 29 39 49 59 69 79 18 66 58 50 42 34 26 75 67 59 28 38 48 58 68 78 27 37 47 51 43 35 76 68 60 52 44 77 57 67 77 36 46 56 66 76 45 69 61 53 78 70 62 79 71 80 55 65 75 54 64 74 63 73 72 2006/11/11 GPW 2006 11 21 31 41 51 61 71 19

Other bitboards Piece promotions Use bitboards that have 1 s for the squares inside the black or white promotion zone Required promotion check Use bitboards to decide if a knight, lance or pawn must promote 2006/11/11 GPW 2006 20
![9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26 9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26](http://slidetodoc.com/presentation_image_h/802b8090b3e9162d6f61ee1147e77746/image-21.jpg)
9 8 7 6 5 4 3 2 1 bb[0] bb[1] bb[2] 2006/11/11 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 GPW 2006 a b c d e f g h i 21

Experimental results Comparing bitboards with attack tables Yamashita showed a 20% speed increase for a tsume shogi solver A different test Minimax search with move generation using bitboards and move generation using attack tables Test conditions Minimax search to depth 4 for 100 positions from two professional games Evaluation function: only material Version Time Attack tables 24810 s Bitboards 12709 s Using bitboards made move generation 48. 8% faster 2006/11/11 GPW 2006 22

Conclusions and Future work Conclusions Bitboards made move generation almost twice as fast Bitboards make a program more transparent Bitboards might be a good alternative to attack tables in shogi as well Future work Will bitboards slow down the evaluation function? The Static Exchange Evaluator and pin analysis can be implemented efficiently with bitboards • Faster than using attack tables? 2006/11/11 GPW 2006 23
- Slides: 23