Using Algebra Tiles to Solve Equations Combine Like

Using Algebra Tiles to Solve Equations, Combine Like Terms, and use the Distributive Property OBJECTIVE: TO UNDERSTAND THE DIFFERENT PARTS OF AN EQUATION, AND USE ALGEBRA TILES TO HELP US SOLVE PROBLEMS.

Important Vocabulary! • Equation – An equation is a mathematical statement that uses an equal sign to show that two expressions have the same value. • To solve an equation that contains a variable, find the value of the variable that makes the equation true. This value of the variable is called the solution of the equation. • Term – the parts of an expression that are added or subtracted. • Like Term – Two or more terms that have the same variable raised to the same power. • Coefficient – The number that is multiplied by a variable in an algebraic expression. • Constant – A value that does not change. • Equivalent Expression – Equivalent expressions have the same value for all values of the variables.

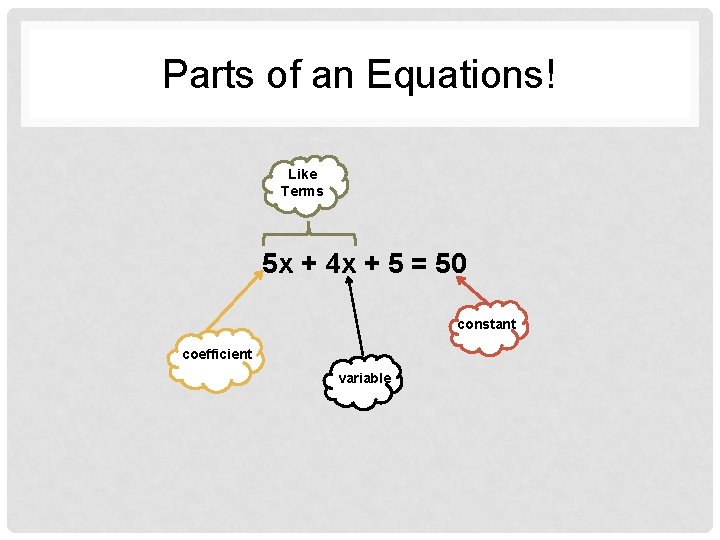
Parts of an Equations! Like Terms 5 x + 4 x + 5 = 50 constant coefficient variable

Your Turn… 6 y + 5 x + 2 y = 42 • Coefficients? • Variables? • Like Terms? • Constant?

Discovery • What do you think the different tiles stand for? Why?

Algebra Tiles What do these stand for? Why?

Let’s Try It • Represent the following equations on your tile mat. Compare your answer with a neighbor. Assist each other as needed. 5+x=2 5 – 5 x = -1 2 x – 5 = 9

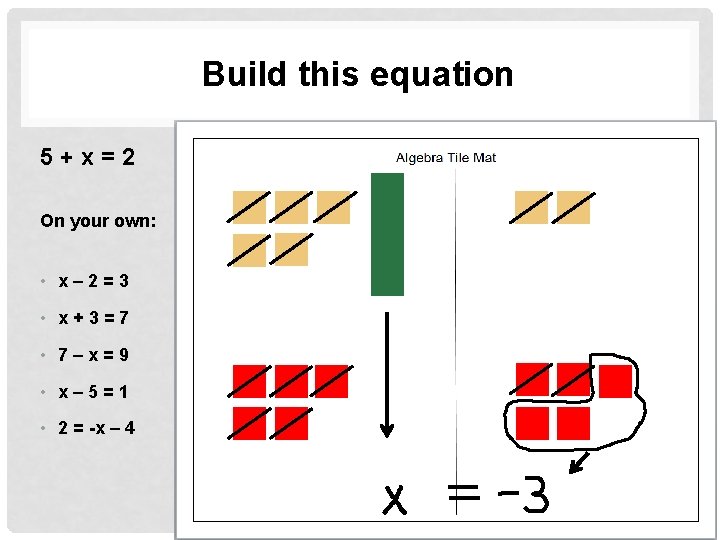
Build this equation 5+x=2 On your own: • x– 2=3 • x+3=7 • 7–x=9 • x– 5=1 • 2 = -x – 4

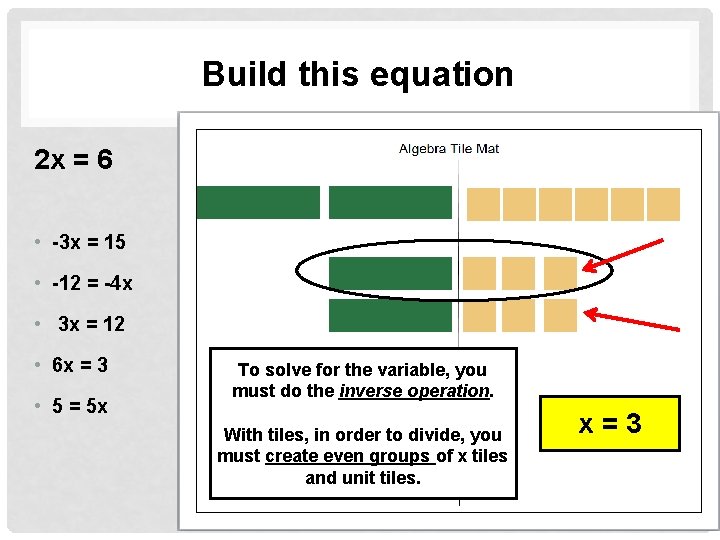
Build this equation 2 x = 6 • -3 x = 15 • -12 = -4 x • 3 x = 12 • 6 x = 3 • 5 = 5 x To solve for the variable, you must do the inverse operation. With tiles, in order to divide, you must create even groups of x tiles and unit tiles. x=3

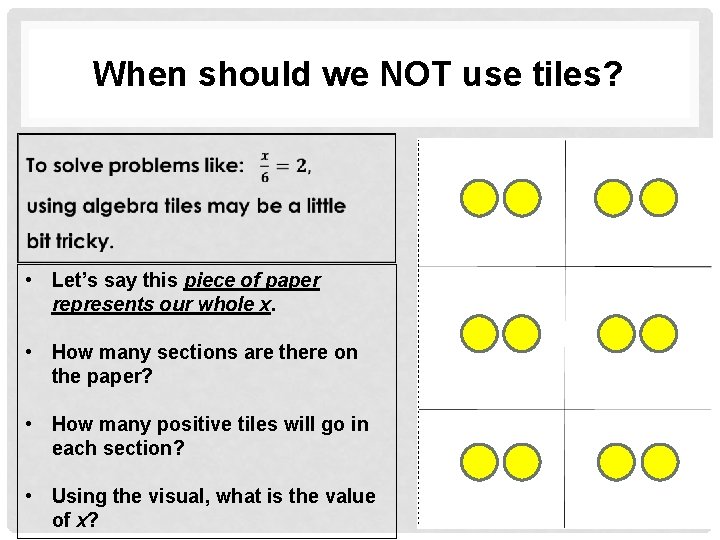
When should we NOT use tiles? • Let’s say this piece of paper represents our whole x. • How many sections are there on the paper? • How many positive tiles will go in each section? • Using the visual, what is the value of x?

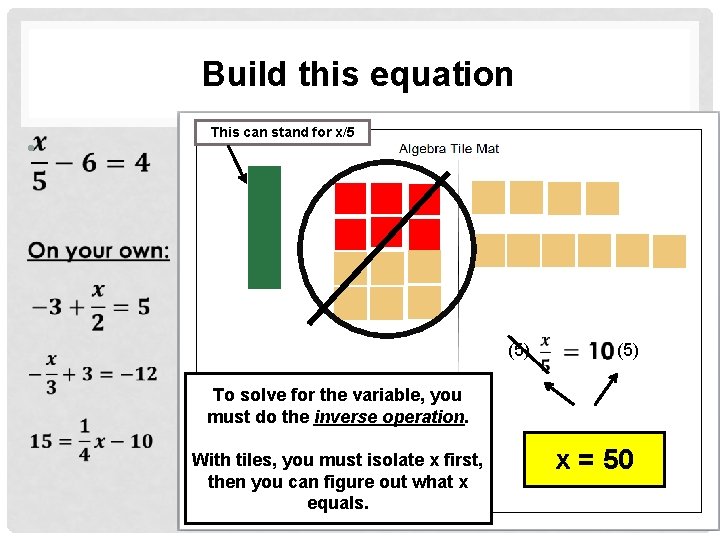
Build this equation • This can stand for x/5 (5) To solve for the variable, you must do the inverse operation. With tiles, you must isolate x first, then you can figure out what x equals. x = 50

Activity… Use your algebra tile mat and algebra tiles, to solve the following equations. 2 x – 3 = 9 5 – 5 x = -1 Zero pairs 3 x – 1 = 8 7 = 5 x + 2 2 x + 3 = 3 x 4 x – 2 = 3 x + 6 Make even groups with each x x=6

Summary! • How will algebra tiles be useful to you in solving equations and combining like terms?

Combining Like Terms What does this tile represent? x 2 -x 2 What does this tile represent? What do these tiles represent? x -x 1 -1

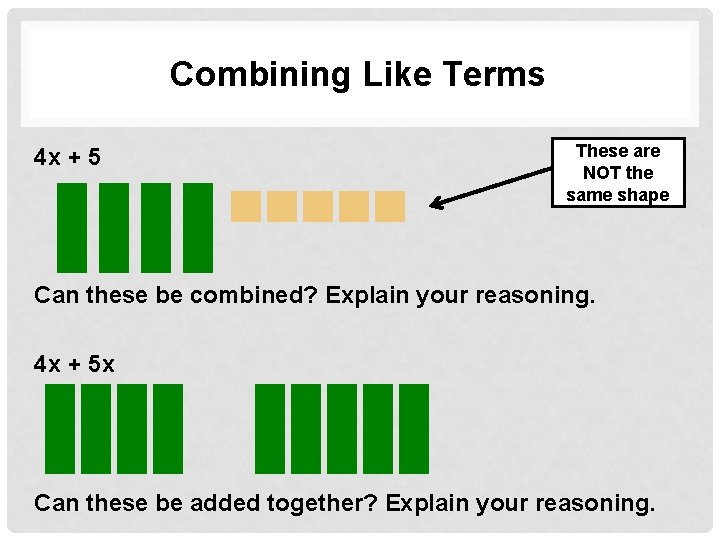
Combining Like Terms 4 x + 5 These are NOT the same shape Can these be combined? Explain your reasoning. 4 x + 5 x Can these be added together? Explain your reasoning.

Let’s Try It! Represent the following expressions on your tile mat. Compare your answer with a neighbor. Assist each other as needed. 3 x + 4 – 2 x 3 x + 5 2 x 2 – 6 x +2 x 2 – 2 x – 3 3 x 2 + 3 x – 5 x

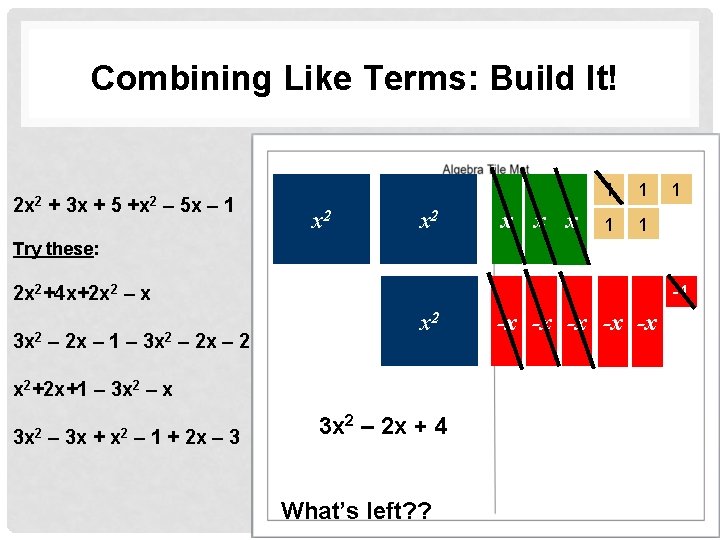
Combining Like Terms: Build It! 2 x 2 + 3 x + 5 +x 2 – 5 x – 1 x 2 x x x 1 1 1 Try these: -1 2 x 2+4 x+2 x 2 – x 3 x 2 – 2 x – 1 – 3 x 2 – 2 x – 2 x 2+2 x+1 – 3 x 2 – x 3 x 2 – 3 x + x 2 – 1 + 2 x – 3 3 x 2 – 2 x + 4 What’s left? ? -x -x -x

Summary • Write 2 – 3 sentences explaining how you use algebra tiles to combine like terms. Pretend you are teaching this concept to a 4 th grader.

Distributive Property • Using algebra tiles, we will use Distributive Property to help us combine like terms and solve equations. • Distributive Property - The property that states that if you multiply a sum by a number, you will get the same result if you multiply each addend by that number and then add the products.

How does it work? Represent the following expression using algebra tiles: 3 (x + 2) 3 groups of x plus 2 When we group our like tiles, what expression do we have? 3 (x + 2) = 3 x + 6

Let’s Practice! Simplify the following expressions: 2(x – 4) 2 groups of x – 4 On your own: (2 x + 1)4 6(-x – 2) + 3 = 2 x – 8 (3 – 2 x)3 + x After grouping like tiles, what do we have?

Distributive Property and Equations Use distributive property to solve the following equations! 2(x + 3) = 10 You try: (-x – 4)3 = 3 2 + 2(2 x – 3) = 8 4 = 3 x – (-x + 3)2 x=2 After making zero pairs, we are left with 2 x’s And 4 unit tiles. What does x equal?

Summary • Pair up with a partner. Each partner will make up a problem that uses the concepts learned in today’s lesson. Switch problems with your partner and solve.