Using A Multiscale Approach to Characterize Workload Dynamics

Using A Multiscale Approach to Characterize Workload Dynamics Tao Li Dept. of Electrical and Computer Engineering University of Florida taoli@ece. ufl. edu June 4, 2005 1

Motivation § Workload dynamics reveals the changing of workload behavior over time § Understanding workload dynamics is important § emerging workload characterization § long-run (servers, e-commerce) § interactive (user, OS, DLL…) § non-deterministic (multithreaded) § run-time tuning, optimization, monitoring § performance, power, reliability, security § microarchitecture trends § CMP, SMT 2

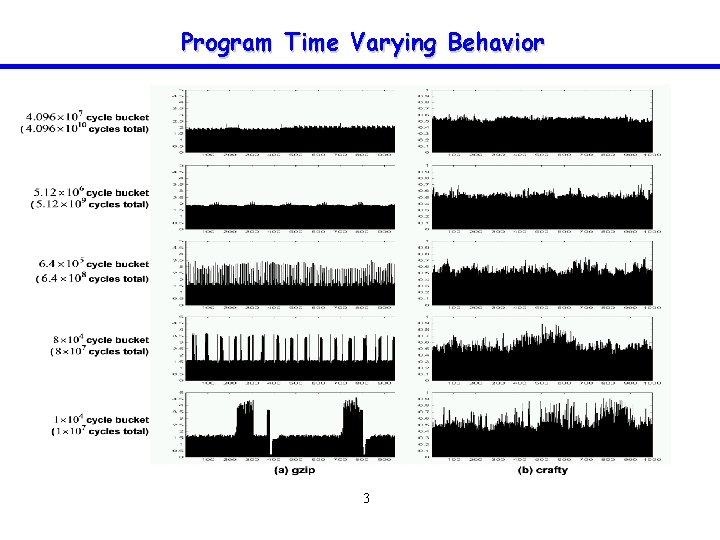
Program Time Varying Behavior 3

Multiscale Workload Characterization § Characterize workload behavior across different time scales § “zoom-in” and “zoom-out” features § Apply wavelet analysis to study program scaling behavior § compact and parsimonious models § Complement with other approaches (aggregate measurement, phase analysis) 4

Outline § Scaling models and wavelet analysis § Experimental setup § Results of SPEC 2 K integer benchmarks § On-line program scaling estimation § Conclusions 5

Scaling Models § Self-similarity: a dilated portion of the sample path of a process can not be statistically distinguished from the whole § H (Hurst parameter): the degree of self-similarity 6

Scaling Models (Contd. ) § Long-Range Dependence (LRD): the correlation function of a process behaves like a power-law of the time lag k is a positive constant and the Hurst parameter § LRD: correlations decay so slowly that they sum to infinity 7

Scaling Analysis Technique: Discrete Wavelet Transform § Consider a series time scale resolution at the finest level of We can coarsen this event series by averaging (with a slightly unusual normalization factor) over non-overlapping blocks of size two (Equ. 1) and generates a new time series X 1, which represents a coarser granularity picture of the original series X 0 8

Discrete Wavelet Transform § The difference between the two, known as details, is (Equ. 2) The original time series X 0 can be reconstructed from its coarser representation X 1 by simply adding in the details d 1 Repeat this process, we get 9

Discrete Wavelet Transform (Contd. ) § Discrete wavelet coefficients: the collection of details § Discrete Wavelet Transform (DWT) iteratively uses Equ. 1 and Equ. 2 to calculate all § DWT divides data into a low-pass approximation and a high-pass detail at any level of resolution § The coefficients of wavelet decomposition can be used to study the scale dependent properties of the data 10

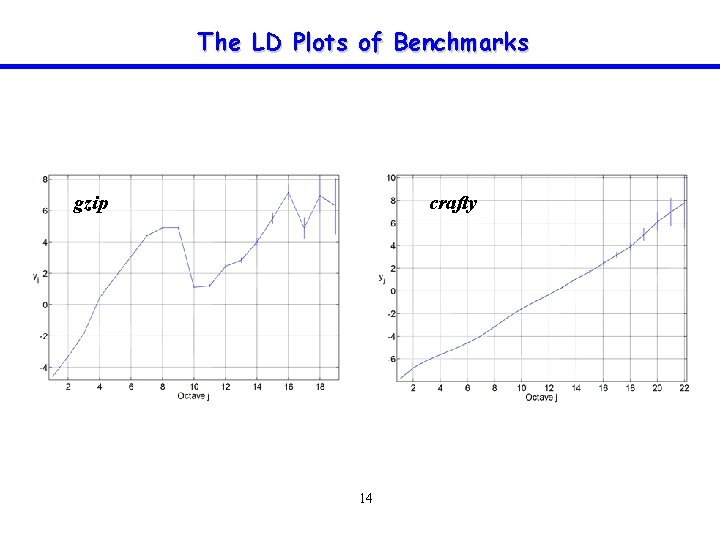
Energy Function and Log-scale Diagram § Given a time series and its discrete wavelet coefficients the average energy at resolution level is then defined as: § The log-scale diagram (LD) is the plot of Ej as a function of resolution level 2 j on a scale, i. e. § The LD plot allows the detection of scaling through observation of strict alignment (linear trend) within some octave range 11

Experimental Setup § Simplescalar 3. 0 Sim-outorder simulator 12

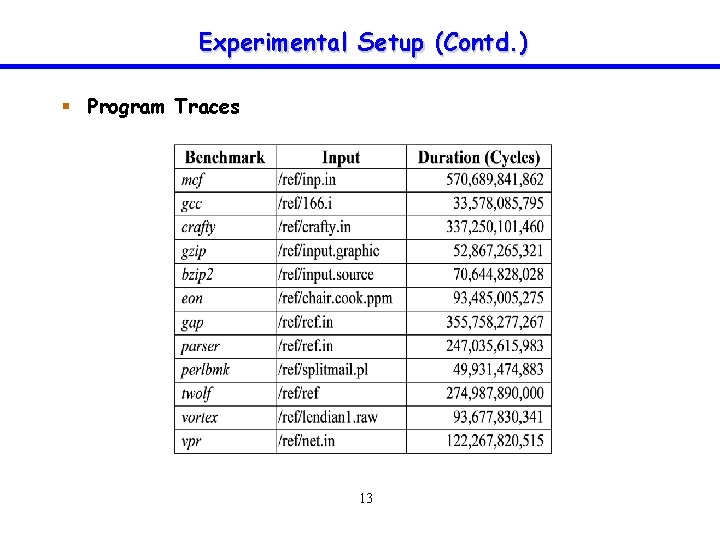
Experimental Setup (Contd. ) § Program Traces 13

The LD Plots of Benchmarks gzip crafty 14

On-line Program Scaling Estimation § Pyramid algorithm for DWT computation 15

On-line Program Scaling Estimation (Contd. ) § High-pass and low pass filters 16

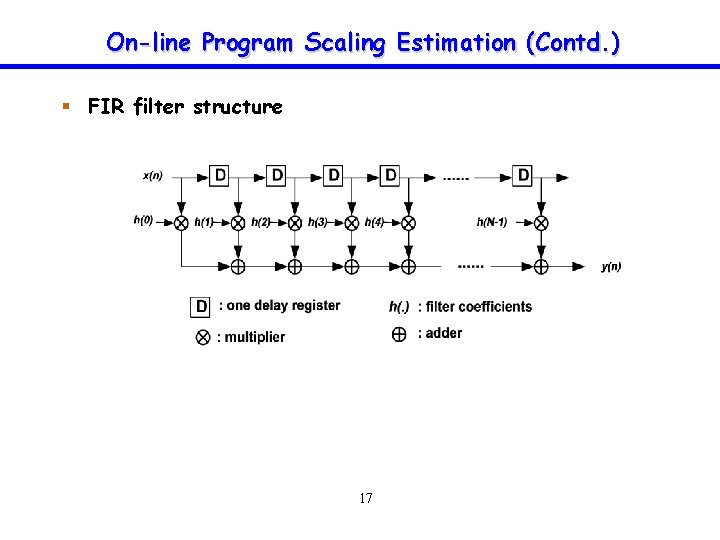
On-line Program Scaling Estimation (Contd. ) § FIR filter structure 17

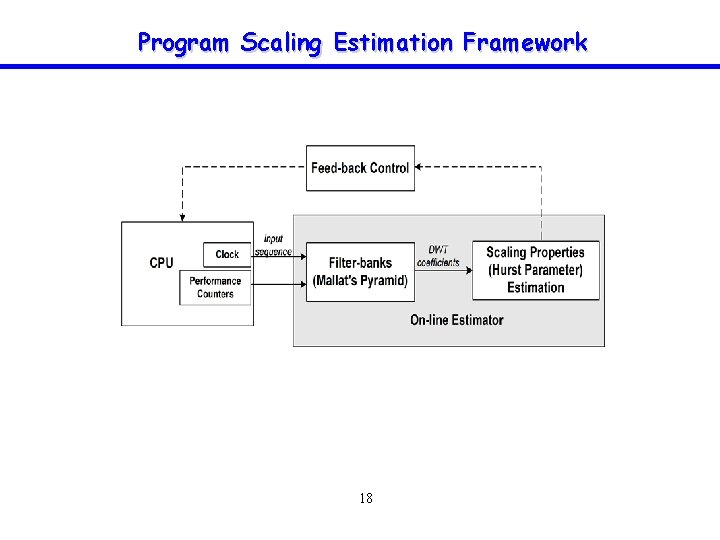
Program Scaling Estimation Framework 18

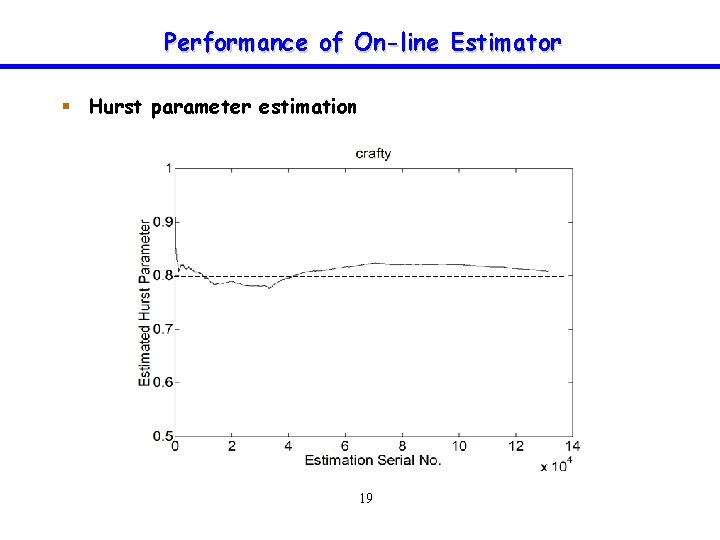
Performance of On-line Estimator § Hurst parameter estimation 19

Conclusions § As software execution cycles become larger, its changing nature can span across a wide range of time scales § Various scaling properties can be used as a useful tool for unraveling the program dynamics over different time periods 20