Use trace algebra to formalize the YAPI model

Use trace algebra to formalize the YAPI model EE 290 N Spring 2002 Alessandro Pinto Mentors: Roberto Passerone Jerry Burch

Outline v References v Introduction to YAPI v Implication of select v Introduction to Trace Algebra v Traces to model YAPI v Buffer model v Conservative Approximation v Example v Conclusion

References v K. A. Vissers et. al. “YAPI: Application Modeling for Signal Processing System”, DAC 00 v J. Burch, R. Passerone, ASV “Overcoming Heterophobia: Modeling Concurrency in Heterogeneous Systems” v J. Burch, R. Passerone, ASV “Modeling Techniques in Design-by-Refinement Methodologies” v E. A. Lee, T. M. Parks “Dataflow Process Networks” v G. Kahn, “The Semantics of a Simple Language for Parallel Programming” v G. Kahn, D. B. Mac. Queen, “Corutines and Networks of Parallel Processes”

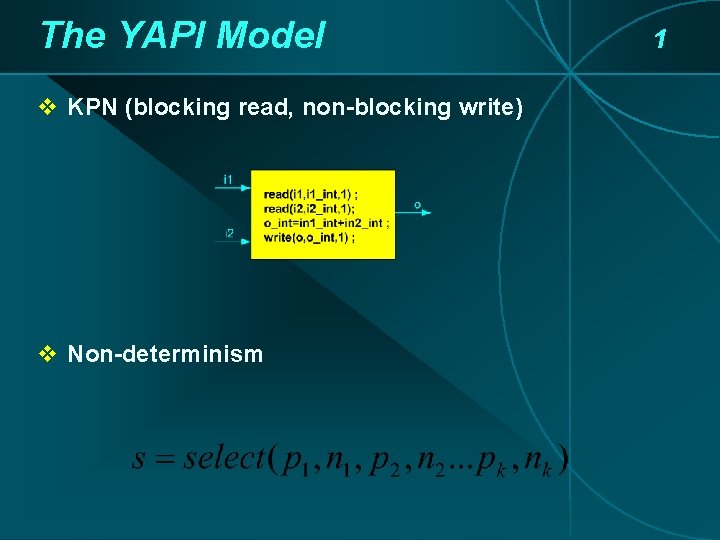
The YAPI Model v KPN (blocking read, non-blocking write) v Non-determinism 1

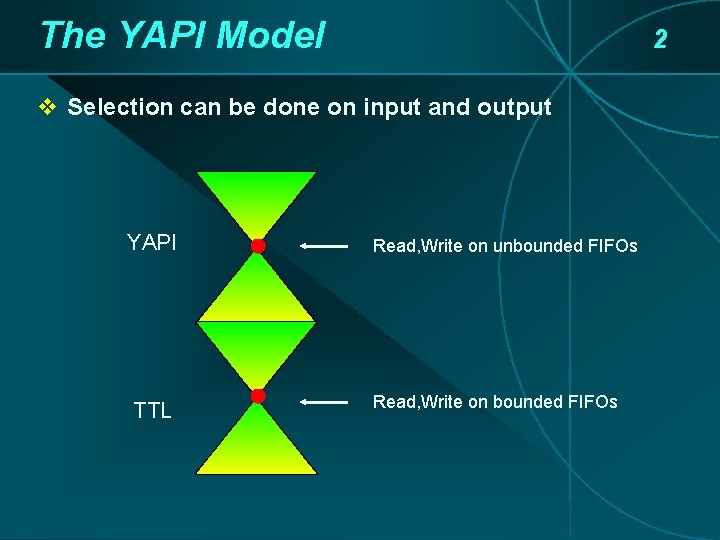
The YAPI Model 2 v Selection can be done on input and output YAPI TTL Read, Write on unbounded FIFOs Read, Write on bounded FIFOs

Implication of select v continuity monotonicity determinacy i 1=[1], i 2=[ ] i 1=[1, 1], i 2=[2] F(i 1, i 2) = [1] F(i 1, i 2) = [2, 1] i=[1] F(i) = ([1], [ ]) i=[1, 3] F(i) = ([1], [3]), ([3], [1]), ([1, 3], [ ]) …

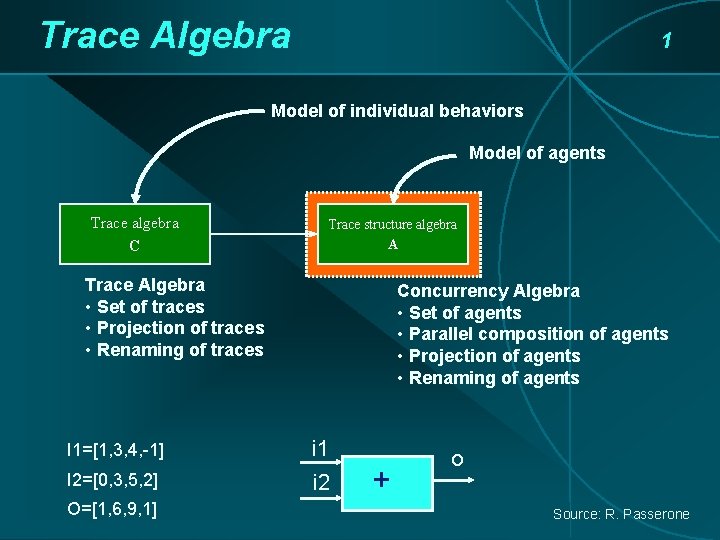
Trace Algebra 1 Model of individual behaviors Model of agents Trace algebra C Trace structure algebra A Trace Algebra • Set of traces • Projection of traces • Renaming of traces Concurrency Algebra • Set of agents • Parallel composition of agents • Projection of agents • Renaming of agents I 1=[1, 3, 4, -1] i 1 I 2=[0, 3, 5, 2] i 2 O=[1, 6, 9, 1] + o Source: R. Passerone

Trace Algebra 2 v Alphabet v Set of traces over alphabet A v Renaming y = rename(r) (x) where x is a trace and r is a renaming function v Projection B A y = proj(B)(x) where x is a trace and v Trace structure and P B(A) T=( , P) where is the signature v A set of axioms must be verified !!!!!!!

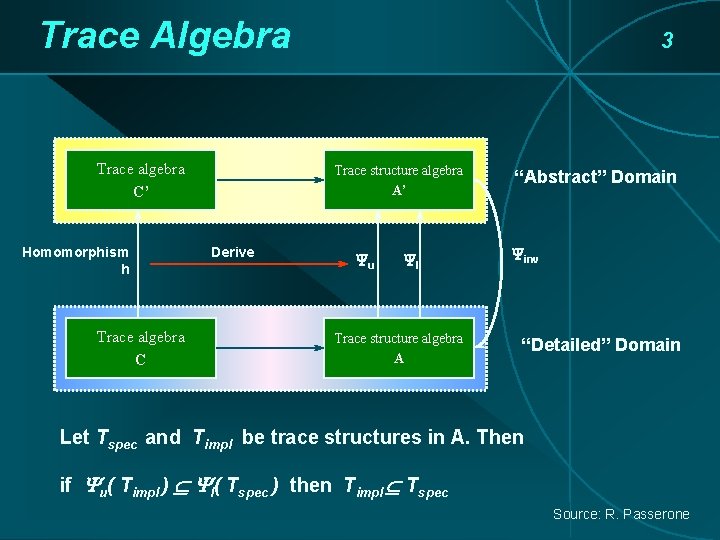
Trace Algebra Trace algebra C’ Homomorphism h Trace algebra C 3 Trace structure algebra A’ Derive Yu Yl Trace structure algebra A “Abstract” Domain Yinv “Detailed” Domain Let Tspec and Timpl be trace structures in A. Then if Yu( Timpl ) Yl( Tspec ) then Timpl Tspec Source: R. Passerone

Implication of select: Trace Algebra View v Monotonicity is captured by projection u proj(I)(x) ⊑ proj(I)(y) proj(O)(x) ⊑ proj(O)(y) v For the previous example two traces belongs to the same process:

First step: Set of Traces v Which set of traces should we choose? u Streams u Synchronous u DE

Streams 1 v No timing information v KPN can be expressed on the same set of traces u Continuity is a constraint on the trace structures v In this sense YAPI processes can form more trace structures then KPN YAPI KPN

Streams v Operation on traces u Renaming u Projection v Operation on trace structures 2

A more detailed domain v We want to capture two important things u Relative arrival time u Bounded FIFOs v Synchronous Domain 1

A more detailed domain v Renaming v Projection Two possible traces 2

Buffers v Buffers are modeled as processes v The strict version of a sequence a is v We indicate with ak the sequence up to instant k v Definition of a buffer u Trace structure TB=((I, O), P)

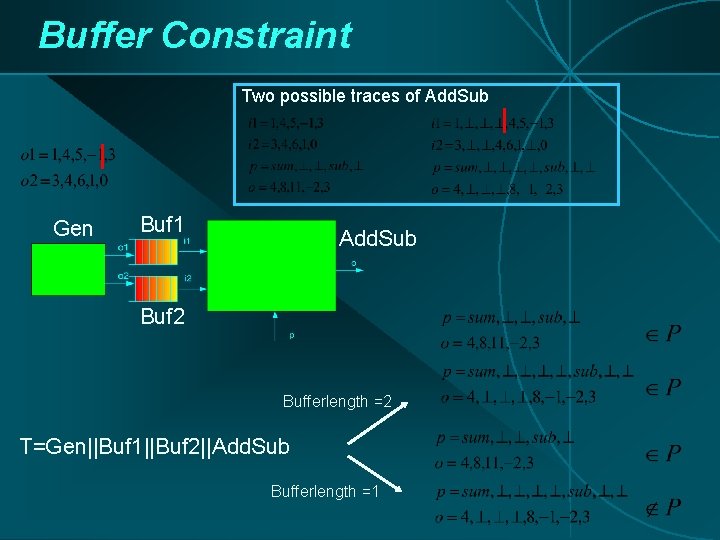
Buffer Constraint Two possible traces of Add. Sub Gen Buf 1 Add. Sub Buf 2 Bufferlength =2 T=Gen||Buf 1||Buf 2||Add. Sub Bufferlength =1

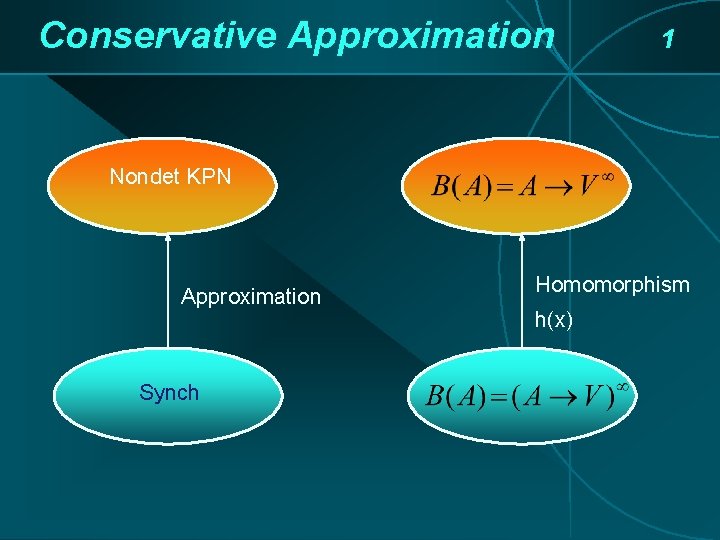
Conservative Approximation 1 Nondet KPN Approximation Synch Homomorphism h(x)

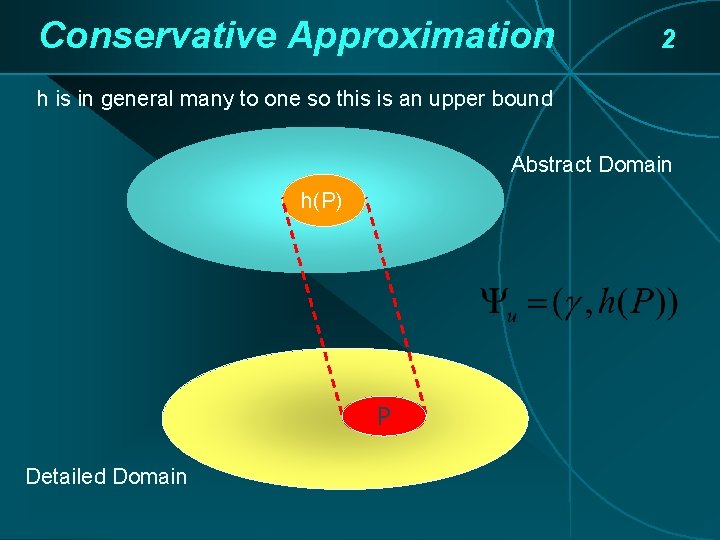
Conservative Approximation 2 h is in general many to one so this is an upper bound Abstract Domain h(P) P Detailed Domain

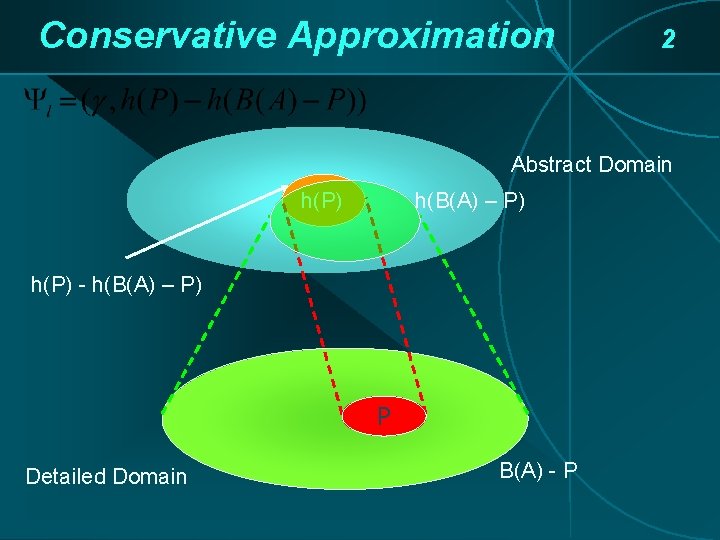
Conservative Approximation 2 Abstract Domain h(P) h(B(A) – P) h(P) - h(B(A) – P) P Detailed Domain B(A) - P

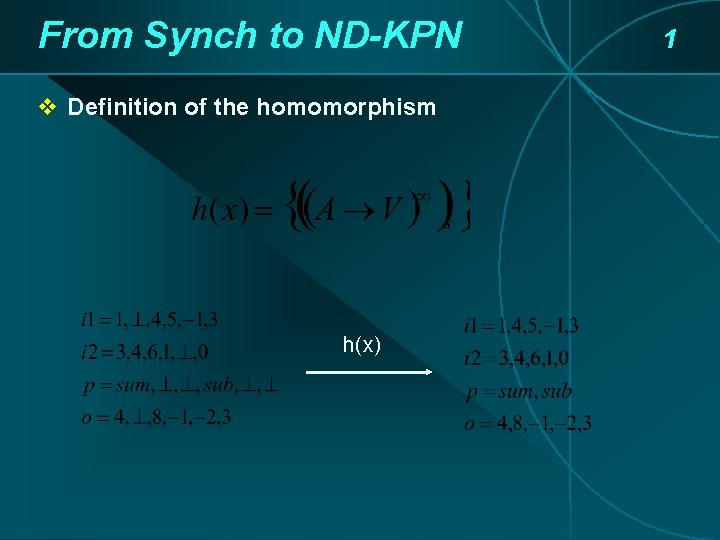
From Synch to ND-KPN v Definition of the homomorphism h(x) 1

From Synch to ND-KPN v v Let’s consider a process: u If p is true add the inputs, if p is false subtract them h(x) 2

Applications of the Approximation v Verification Problem v Design Problem

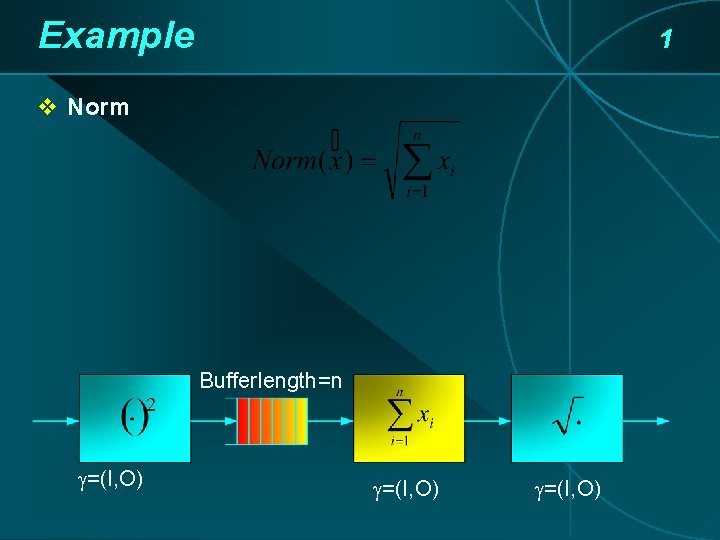
Example 1 v Norm Bufferlength=n =(I, O)

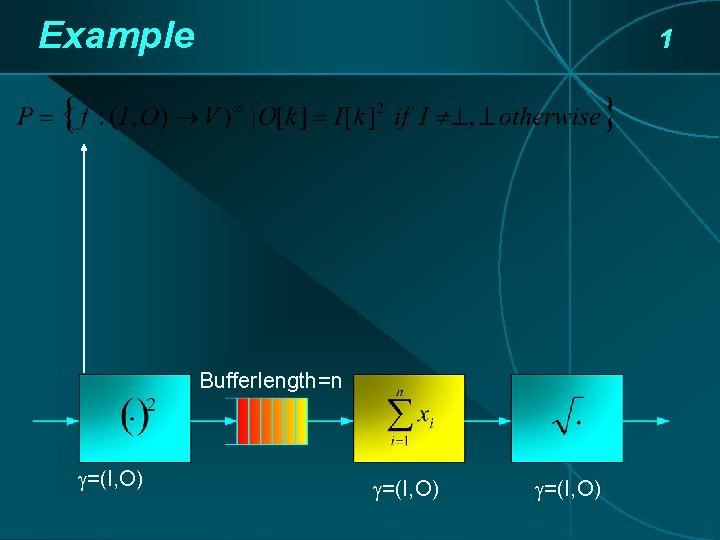
Example 1 Bufferlength=n =(I, O)

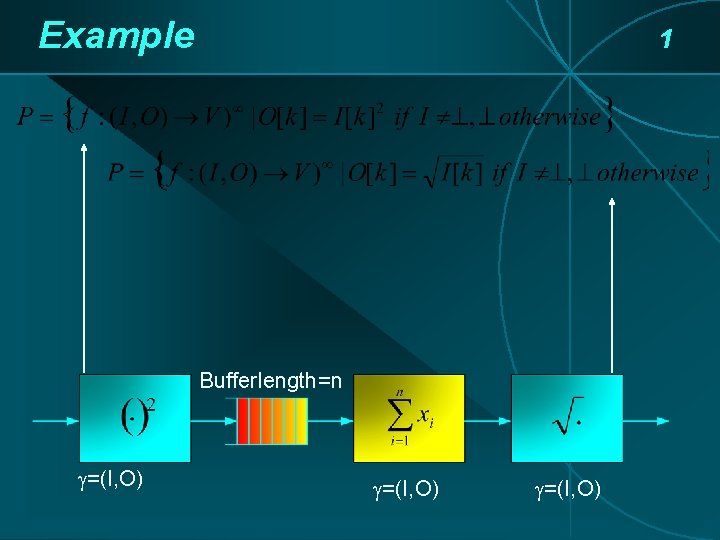
Example 1 Bufferlength=n =(I, O)

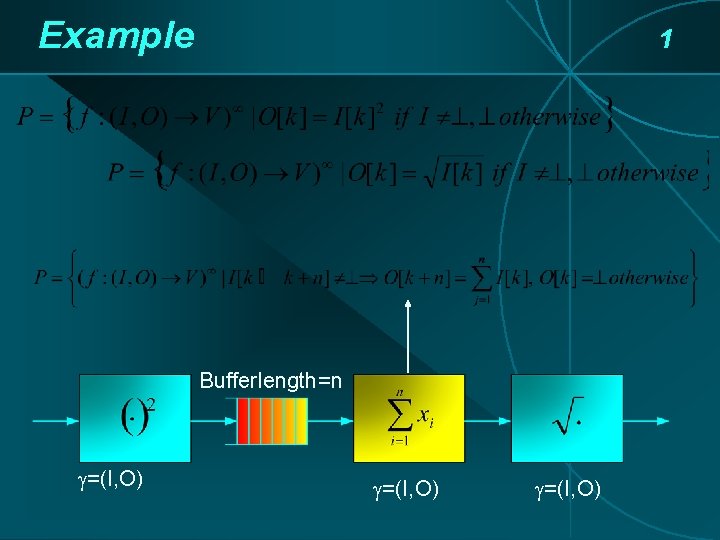
Example 1 Bufferlength=n =(I, O)

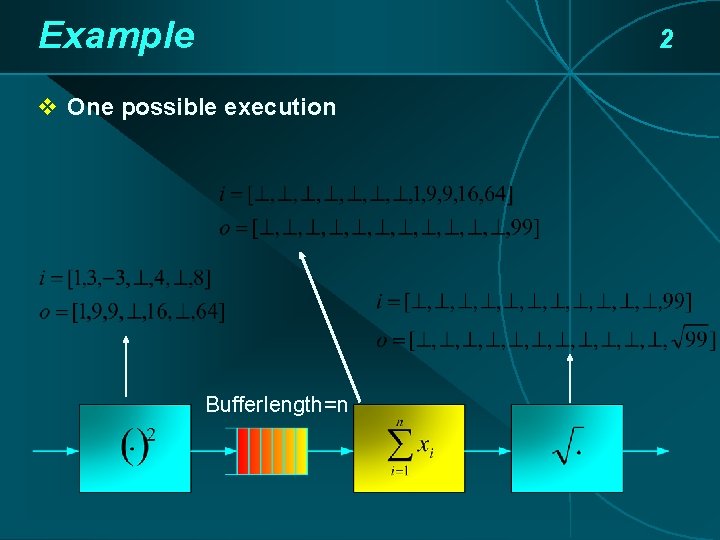
Example 2 v One possible execution Bufferlength=n

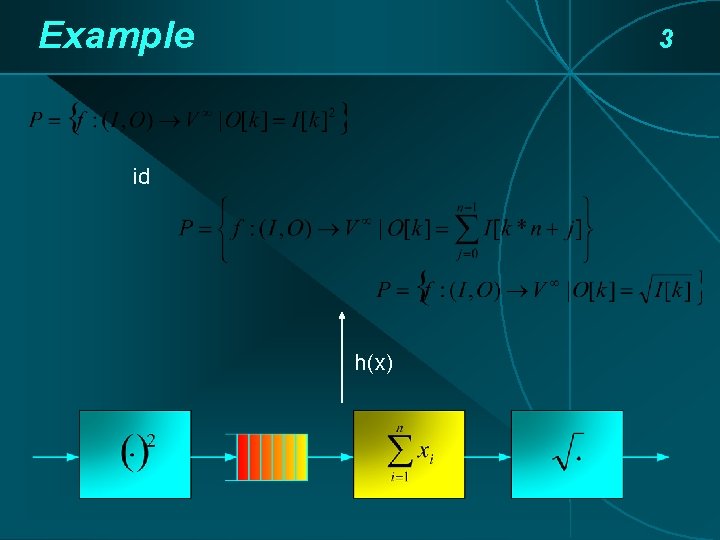
Example 3 id h(x)

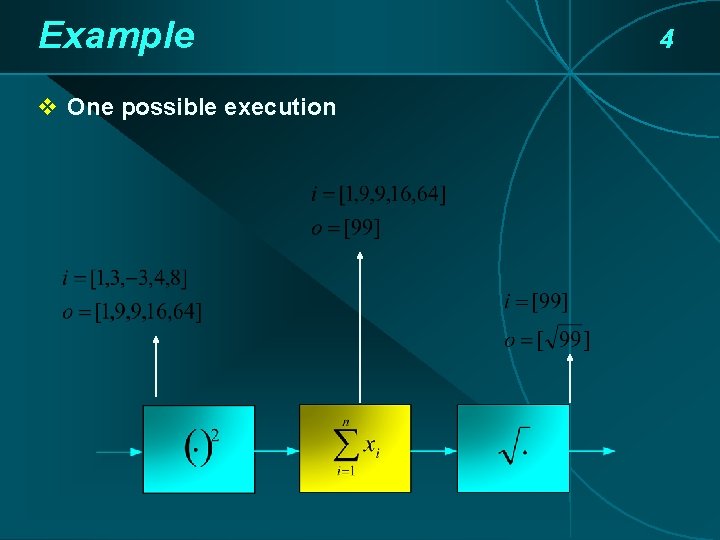
Example v One possible execution 4

Example v Design problem 4

Conclusion v The YAPI model was a good motivation for this project v Trace algebra has been applied to describe the denotational semantics of the model at different level of abstraction v A Conservative approximation between Synchronous model and ND-KPN allows abstraction from one model to another for verification and design