Use the SSS Postulate to test for triangle

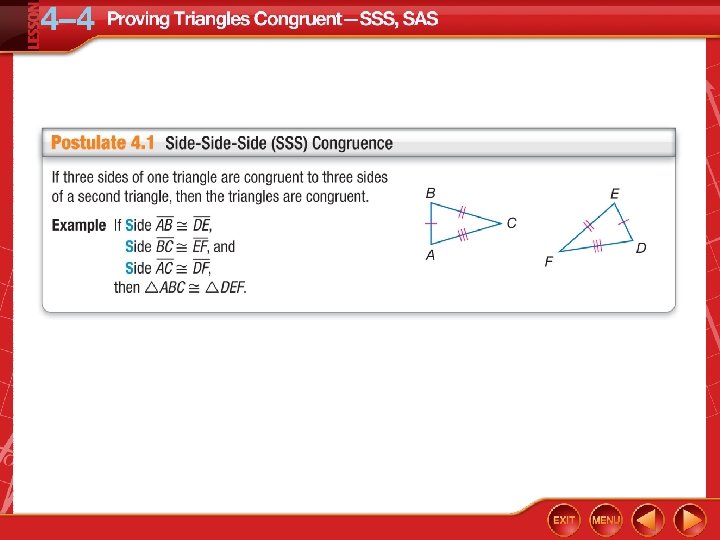
• Use the SSS Postulate to test for triangle congruence. • Use the SAS Postulate to test for triangle congruence.

Content Standards G. CO. 10 Prove theorems about triangles. G. SRT. 5 Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. Mathematical Practices 3 Construct viable arguments and critique the reasoning of others. 1 Make sense of problems and persevere in solving them.

• included angle

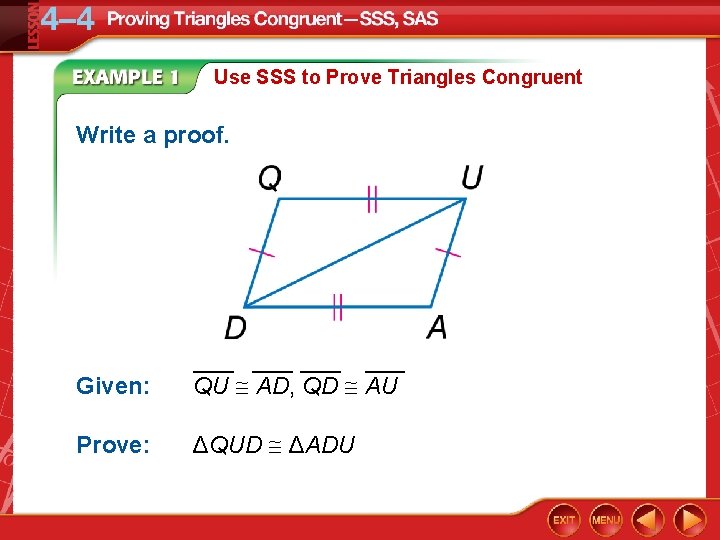
Use SSS to Prove Triangles Congruent Write a proof. Given: ___ ___ QU AD, QD AU Prove: ΔQUD ΔADU

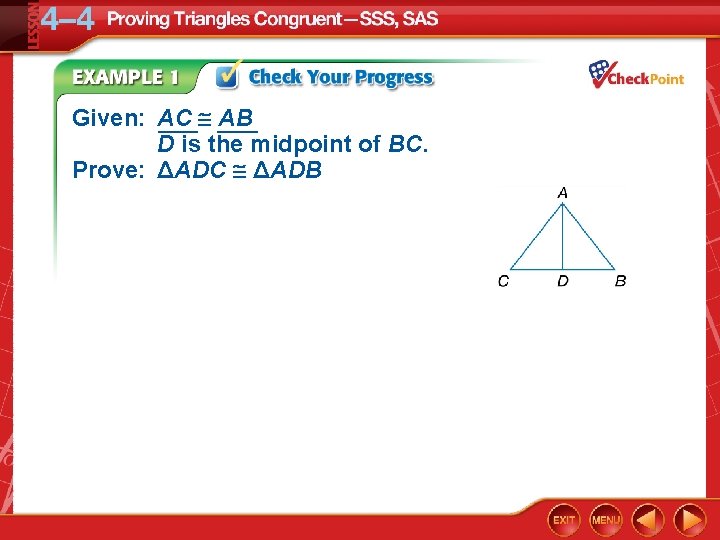
Given: AC AB ___ D is the midpoint of BC. Prove: ΔADC ΔADB

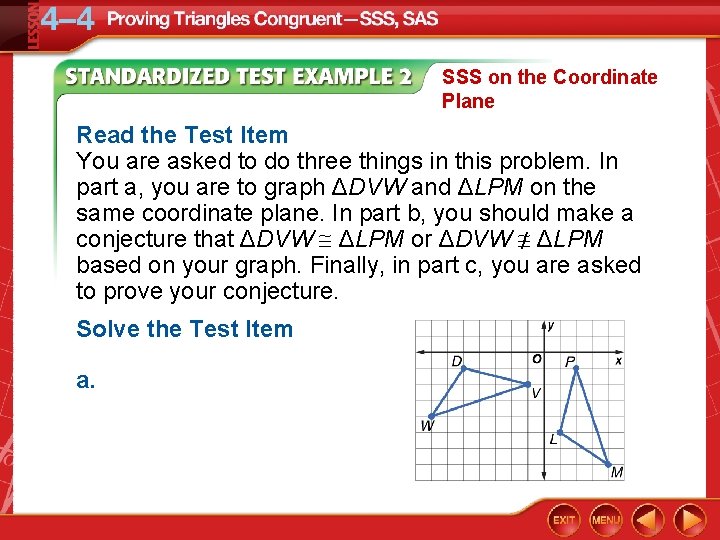
SSS on the Coordinate Plane EXTENDED RESPONSE Triangle DVW has vertices D(– 5, – 1), V(– 1, – 2), and W(– 7, – 4). Triangle LPM has vertices L(1, – 5), P(2, – 1), and M(4, – 7). a. Graph both triangles on the same coordinate plane. b. Use your graph to make a conjecture as to whether the triangles are congruent. Explain your reasoning. c. Write a logical argument that uses coordinate geometry to support the conjecture you made in part b.

SSS on the Coordinate Plane Read the Test Item You are asked to do three things in this problem. In part a, you are to graph ΔDVW and ΔLPM on the same coordinate plane. In part b, you should make a conjecture that ΔDVW ΔLPM or ΔDVW / ΔLPM based on your graph. Finally, in part c, you are asked to prove your conjecture. Solve the Test Item a.

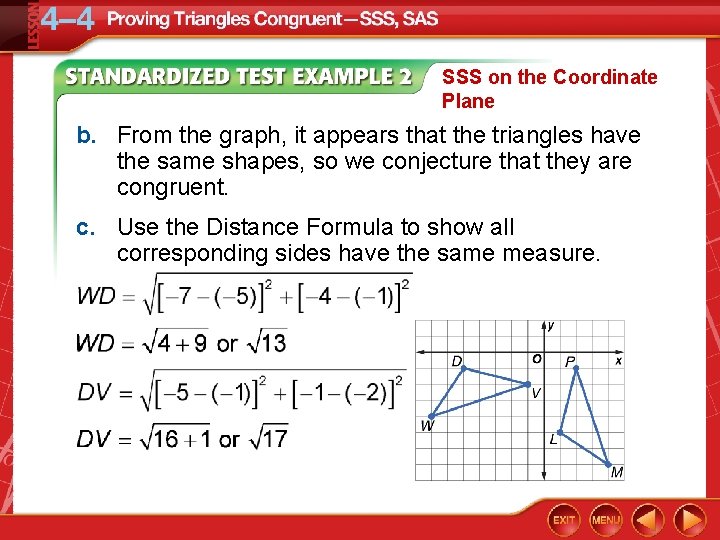
SSS on the Coordinate Plane b. From the graph, it appears that the triangles have the same shapes, so we conjecture that they are congruent. c. Use the Distance Formula to show all corresponding sides have the same measure.

SSS on the Coordinate Plane

SSS on the Coordinate Plane Answer: WD = ML, DV = LP, and VW = PM. By definition of congruent segments, all corresponding segments are congruent. Therefore, ΔDVW ΔLPM by SSS.

Determine whether ΔABC ΔDEF for A(– 5, 5), B(0, 3), C(– 4, 1), D(6, – 3), E(1, – 1), and F(5, 1).

Use SAS to Prove Triangles are Congruent ENTOMOLOGY The wings of one type of moth form two triangles. Write a two-column proof to prove that ΔFEG ΔHIG if EI FH, and G is the midpoint of both EI and FH.

Use SAS to Prove Triangles are Congruent Given: EI FH; G is the midpoint of both EI and FH. Prove: ΔFEG ΔHIG Proof: Statements Reasons

Write a proof to prove that ΔABG ΔCGB if ABG CGB and AB CG. Choose the best reason to fill in the blank. Proof: Statements Reasons

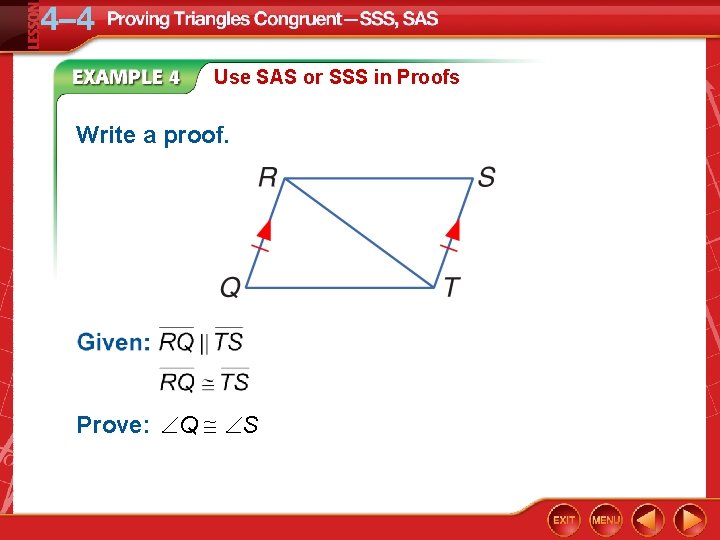
Use SAS or SSS in Proofs Write a proof. Prove: Q S

Homework Page 269 (5, 6, 9, 12, 13)