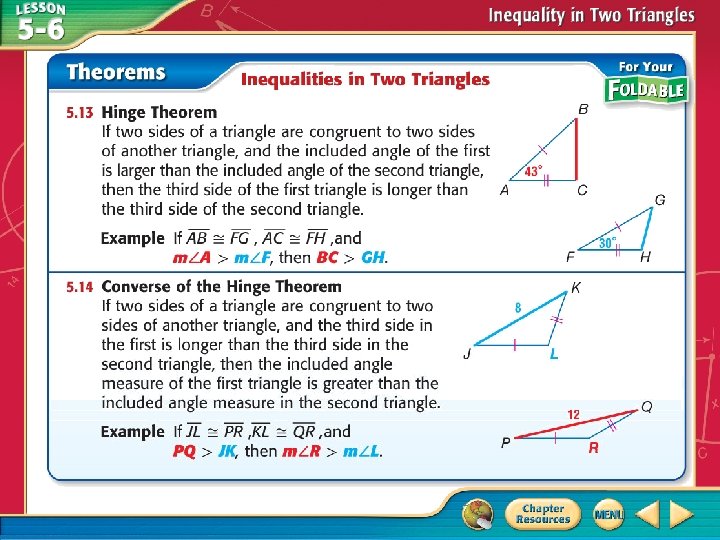
Use the Hinge Theorem and Its Converse A

Use the Hinge Theorem and Its Converse A. Compare the measures AD and BD. In ΔACD and ΔBCD, AC BC, CD CD, and ACD > BCD. Answer: By the Hinge Theorem, m ACD > m BCD, so AD > DB.

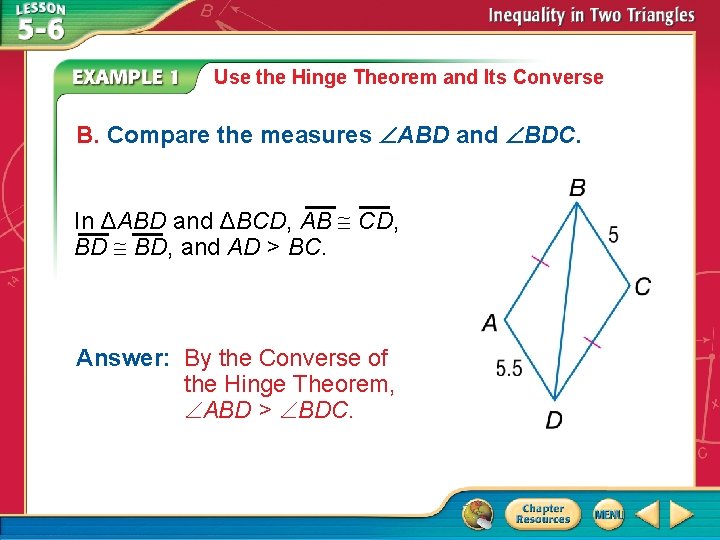
Use the Hinge Theorem and Its Converse B. Compare the measures ABD and BDC. In ΔABD and ΔBCD, AB CD, BD BD, and AD > BC. Answer: By the Converse of the Hinge Theorem, ABD > BDC.

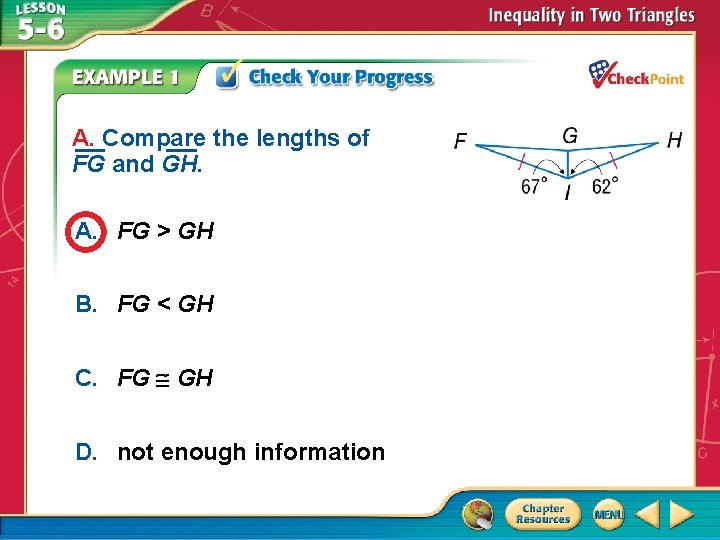
A. Compare the lengths of FG and GH. A. FG > GH B. FG < GH C. FG GH D. not enough information A. B. C. D. A B C D

B. Compare JKM and KML. A. m JKM > m KML B. m JKM < m KML C. m JKM = m KML D. not enough information A. B. C. D. A B C D

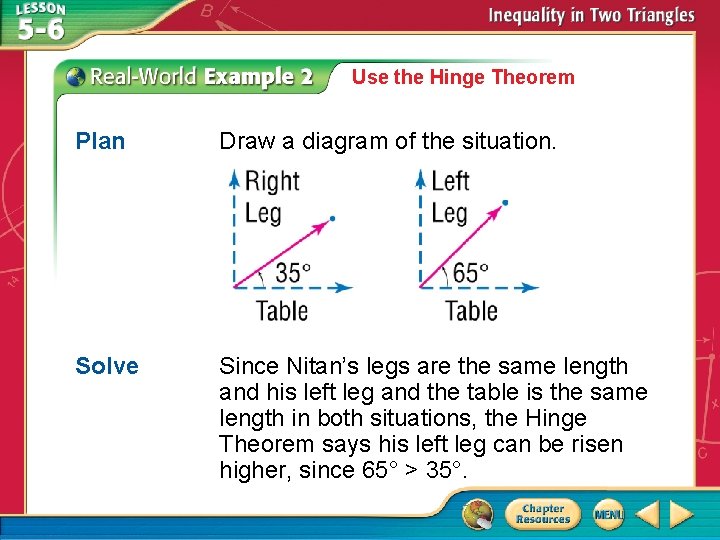
Use the Hinge Theorem HEALTH Doctors use a straight-leg-raising test to determine the amount of pain felt in a person’s back. The patient lies flat on the examining table, and the doctor raises each leg until the patient experiences pain in the back area. Nitan can tolerate the doctor raising his right leg 35° and his left leg 65° from the table. Which leg can Nitan raise higher above the table? Understand Using the angles given in the problem, you need to determine which leg can be risen higher above the table.

Use the Hinge Theorem Plan Draw a diagram of the situation. Solve Since Nitan’s legs are the same length and his left leg and the table is the same length in both situations, the Hinge Theorem says his left leg can be risen higher, since 65° > 35°.

Use the Hinge Theorem Answer: Nitan can raise his left leg higher above the table. Check Nitan’s left leg is pointed 30° more towards the ceiling, so it should be higher that his right leg.

Meena and Rita are both flying kites in a field near their houses. Both are using strings that are 10 meters long. Meena’s kite string is at an angle of 75° with the ground. Rita’s kite string is at an angle of 65° with the ground. If they are both standing at the same elevation, which kite is higher in the air? A. Meena’s kite B. Rita’s kite A. A B. B

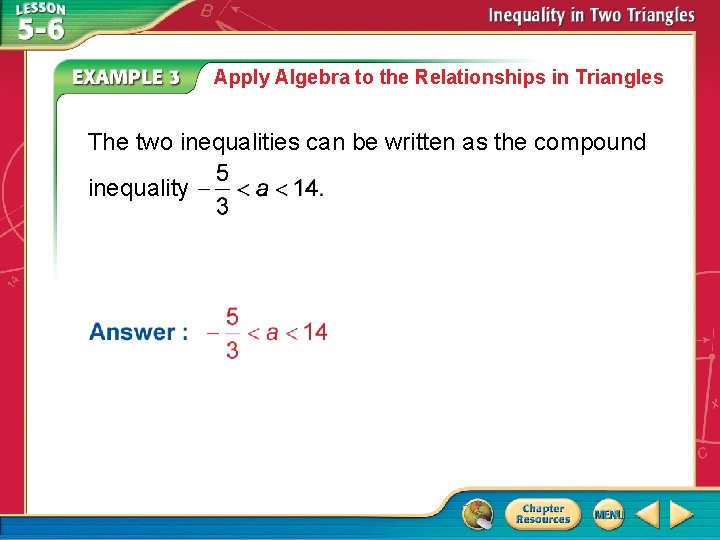
Apply Algebra to the Relationships in Triangles ALGEBRA Find the range of possible values for a. From the diagram we know that

Apply Algebra to the Relationships in Triangles Converse of the Hinge Theorem Substitution Subtract 15 from each side. Divide each side by 9. Recall that the measure of any angle is always greater than 0. Subtract 15 from each side. Divide each side by 9.

Apply Algebra to the Relationships in Triangles The two inequalities can be written as the compound inequality

Find the range of possible values of n. __ A. 6 < n < 12 1 7 B. C. n > 6 D. 6 < n < 18. 3 A. B. C. D. A B C D

Which reason correctly completes the following proof? Given: Prove: AC > DC

Statements Reasons 1. Given 2. Reflexive Property 3. m ABC > m ABD + m DBC 3. Given 4. m ABC > m DBC 4. Definition of Inequality 5. AC > DC 5. ?

A. Substitution B. Isosceles Triangle Theorem C. Hinge Theorem D. none of the above A. B. C. D. A B C D

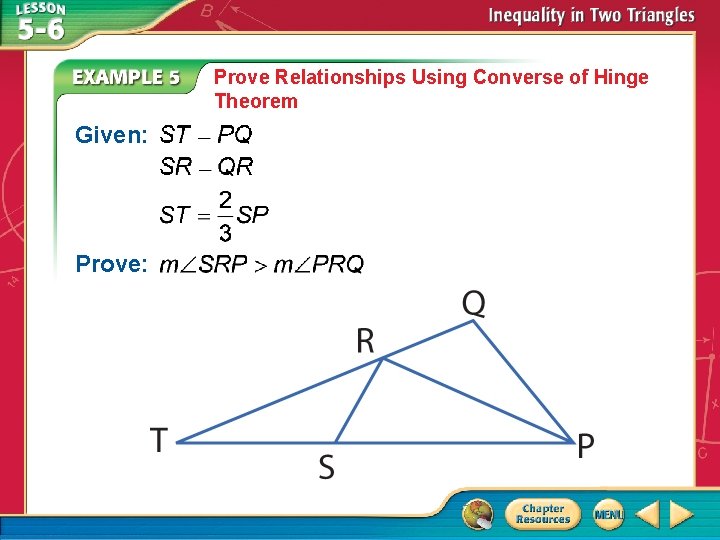
Prove Relationships Using Converse of Hinge Theorem Given: Prove:

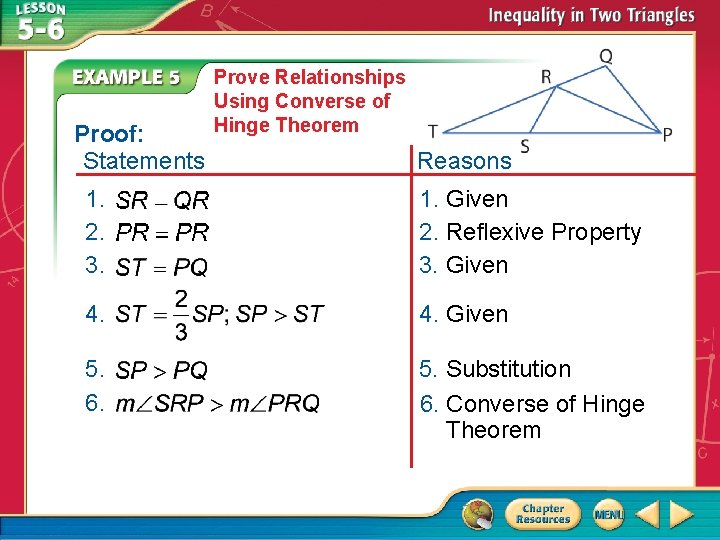
Proof: Statements Prove Relationships Using Converse of Hinge Theorem Reasons 1. 2. 3. 1. Given 2. Reflexive Property 3. Given 4. Given 5. 6. 5. Substitution 6. Converse of Hinge Theorem

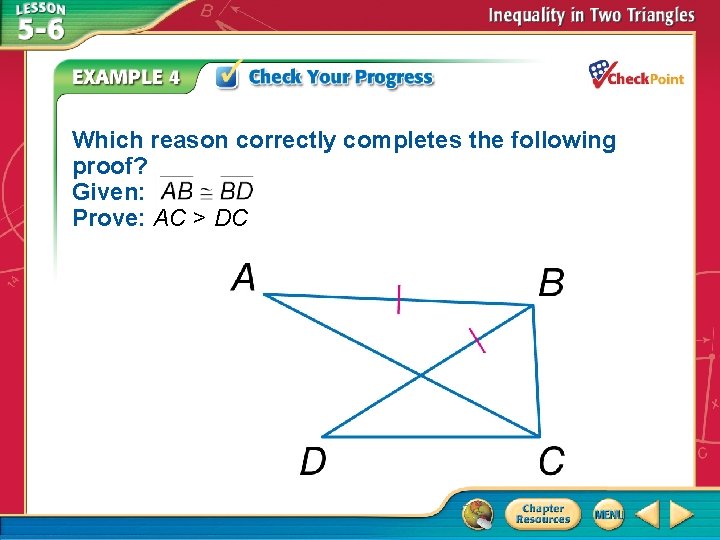
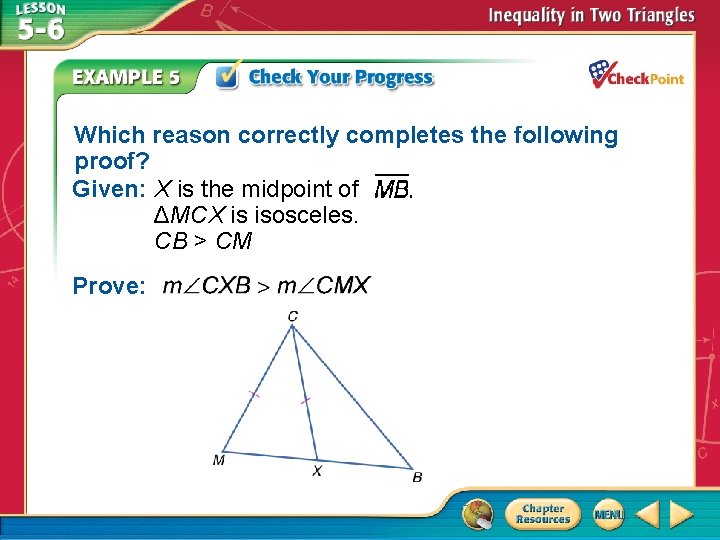
Which reason correctly completes the following proof? Given: X is the midpoint of ΔMCX is isosceles. CB > CM Prove:

Statements 1. X is the midpoint of MB; ΔMCX is isosceles 2. 3. 4. CB > CM 5. m CXB > m CXM 6. 7. 8. m CXB > m CMX Reasons 1. Given 2. Definition of midpoint 3. Reflexive Property 4. Given 5. ? 6. Definition of isosceles triangle 7. Isosceles Triangle Theorem 8. Substitution

A. Converse of Hinge Theorem B. Definition of Inequality C. Substitution D. none of the above A. B. C. D. A B C D