Use of a commercial laser tracker for optical

Use of a commercial laser tracker for optical alignment James H. Burge, Peng Su, Chunyu Zhao, Tom Zobrist College of Optical Sciences Steward Observatory University of Arizona

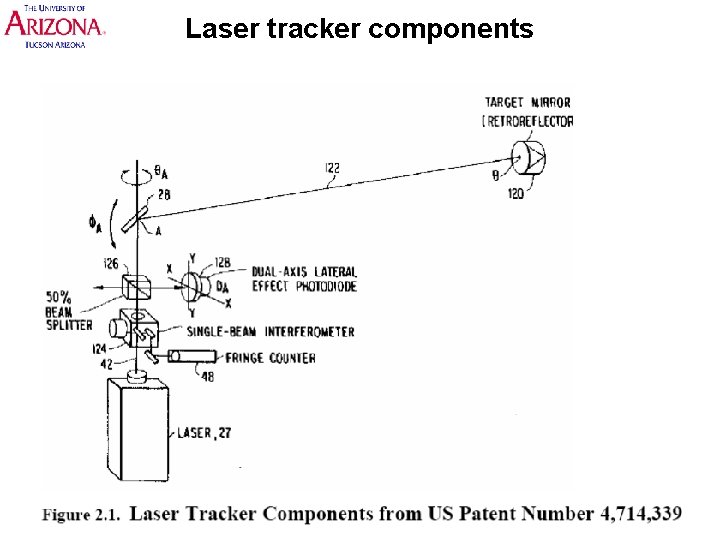
What is a Laser Tracker? Laser Tracker: Optical coordinate measuring machine • Projects a laser beam. Use two-axis gimbals to track the reflection from a corner cube • Measure 3 -space position: – Two pointing angles – Radial distance • ADM (Absolute Distance Measurement) • DMI (Distance measuring interferometer) • SMR – Sphere Mounted Retroreflector (Faro) • Software converts from spherical coordinates

Laser tracker components

Three manufacturers of Laser Trackers • Leica Geosystems (Switzerland) • FARO (USA) • API (USA) 34” 21” 14”

Laser tracker accuracy Assume advertised performance (all values are 2 s) Define z as line of sight direction for tracker Uncertainty in position using ADM is Radial: Lateral x Lz a q z For other directions, use vector projection (Out of plane, Dy, behaves the same as Dx. )

Calibration of laser tracker • Distance Measuring Interferometer gives < 0. 1 µm/m accuracy – Typically limited by air temperature (1°C gives 1 µm/m error. ) • Tracker repeatability is typically < 1 µm/m for all dimensions • The tracker can be calibrated for specific measurements using the DMI. – Radial : use DMI mode, moving the tracker ball – Lateral : use a second tracker in DMI mode • So it is possible to get micron level accuracy – – Need thermal control Control of geometry Careful calibration Average out noise

Special advantages of the laser tracker • • Can achieve micron accuracy (so can CMM) Portable Measure over very large distances Can use optical tricks – Measure through fold mirrors – Measure through windows – Measure angles

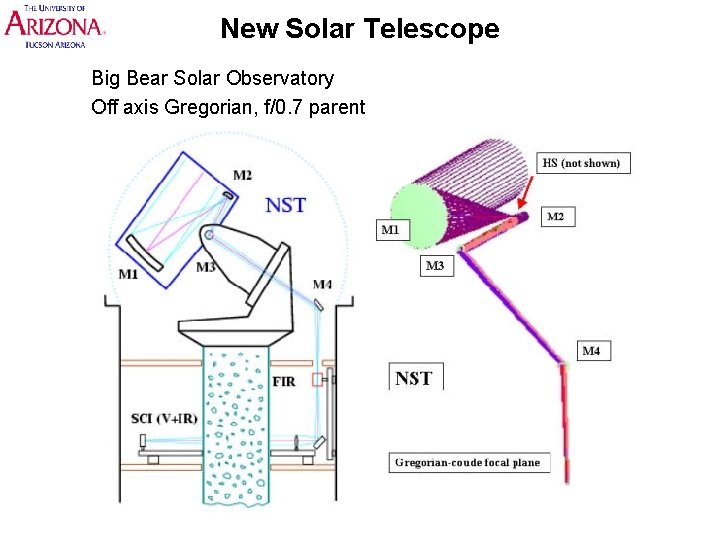
New Solar Telescope Big Bear Solar Observatory Off axis Gregorian, f/0. 7 parent

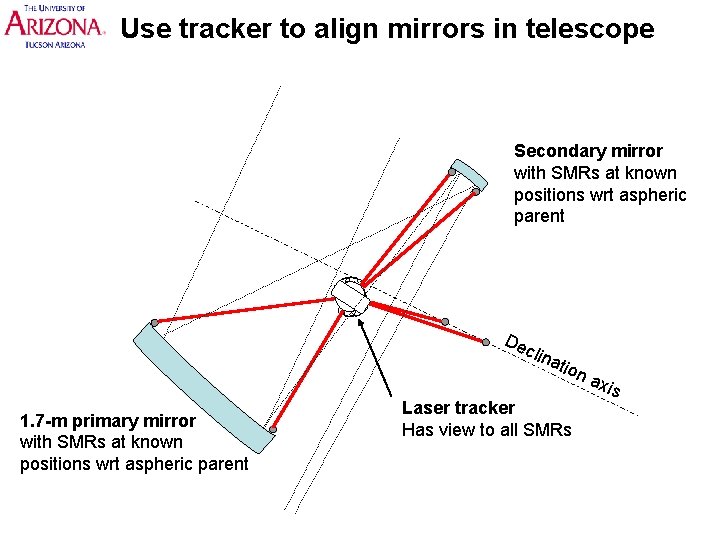
Use tracker to align mirrors in telescope Secondary mirror with SMRs at known positions wrt aspheric parent De clin 1. 7 -m primary mirror with SMRs at known positions wrt aspheric parent atio Laser tracker Has view to all SMRs na xis

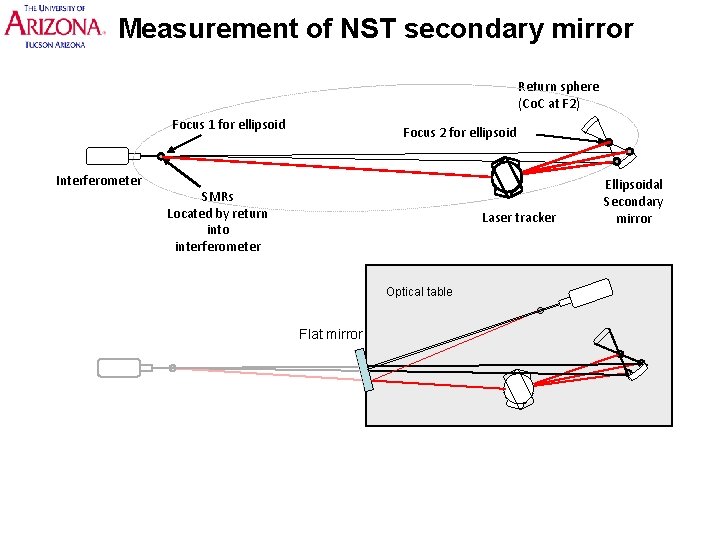
Measurement of NST secondary mirror Return sphere (Co. C at F 2) Focus 1 for ellipsoid Interferometer Focus 2 for ellipsoid SMRs Located by return into interferometer Laser tracker Optical table Flat mirror Ellipsoidal Secondary mirror

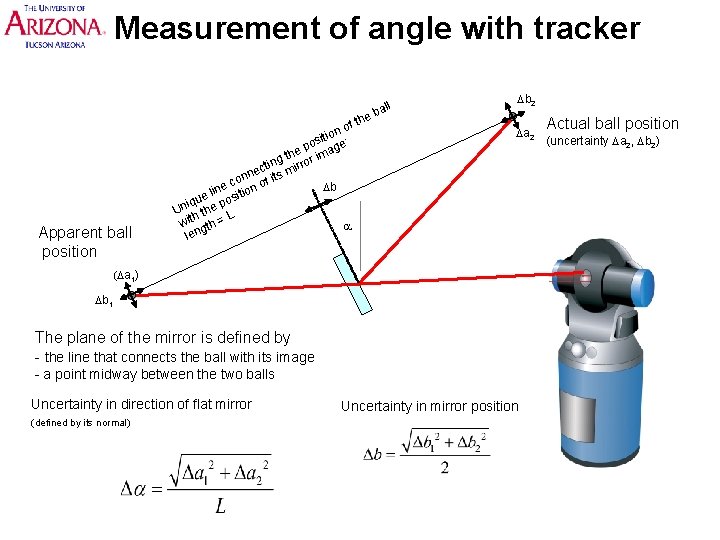
Measurement of angle with tracker he Apparent ball position of t n o iti pos age: e g th rror im n i t ec ts mi n n co n of i Db e n i l tio i e s u iq po Un the L h wit gth = a len l bal Db 2 Da 2 (Da 1) Db 1 The plane of the mirror is defined by - the line that connects the ball with its image - a point midway between the two balls Uncertainty in direction of flat mirror (defined by its normal) Uncertainty in mirror position Actual ball position (uncertainty Da 2, Db 2)

Test of tracker through fold mirrors • Use high quality 12” flat mirror. Compare SMR measurements (actual and apparent). Calculate mirror normal • Measure mirror surface directly by touching the mirror with the SMRs • The two methods agree to within the 1 arcsec stability of the mirror

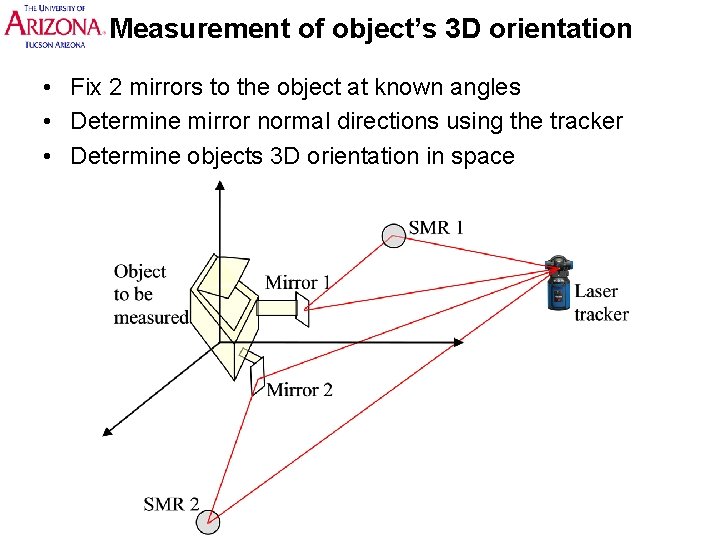
Measurement of object’s 3 D orientation • Fix 2 mirrors to the object at known angles • Determine mirror normal directions using the tracker • Determine objects 3 D orientation in space

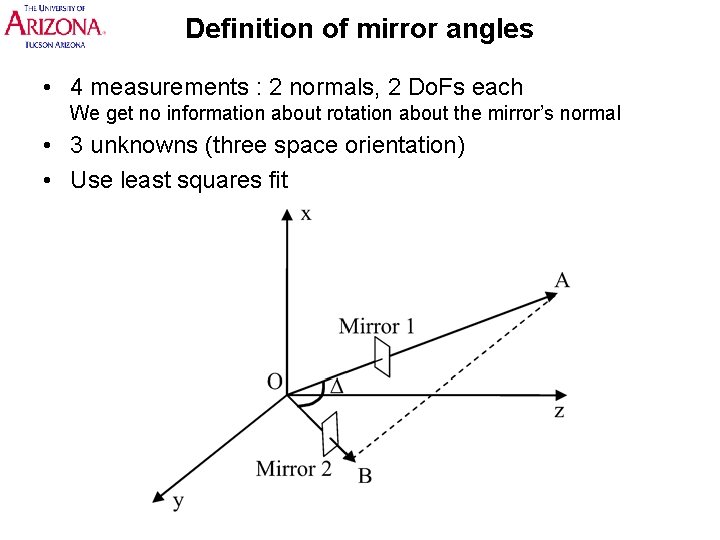
Definition of mirror angles • 4 measurements : 2 normals, 2 Do. Fs each We get no information about rotation about the mirror’s normal • 3 unknowns (three space orientation) • Use least squares fit

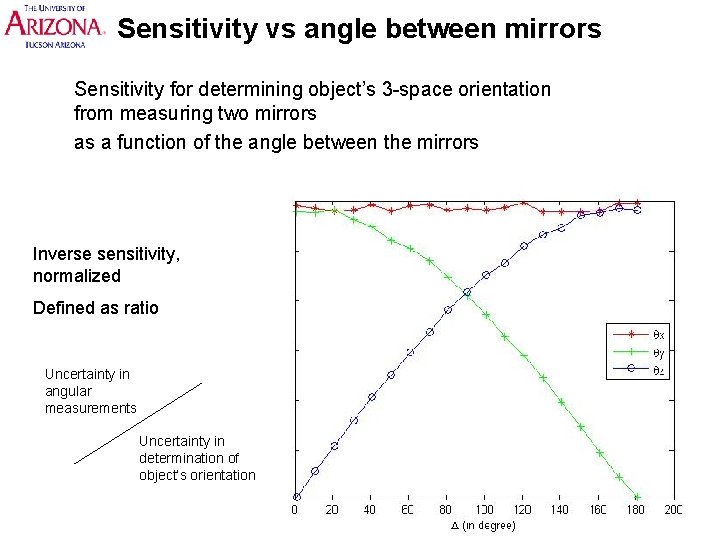
Sensitivity vs angle between mirrors Sensitivity for determining object’s 3 -space orientation from measuring two mirrors as a function of the angle between the mirrors Inverse sensitivity, normalized Defined as ratio Uncertainty in angular measurements Uncertainty in determination of object’s orientation

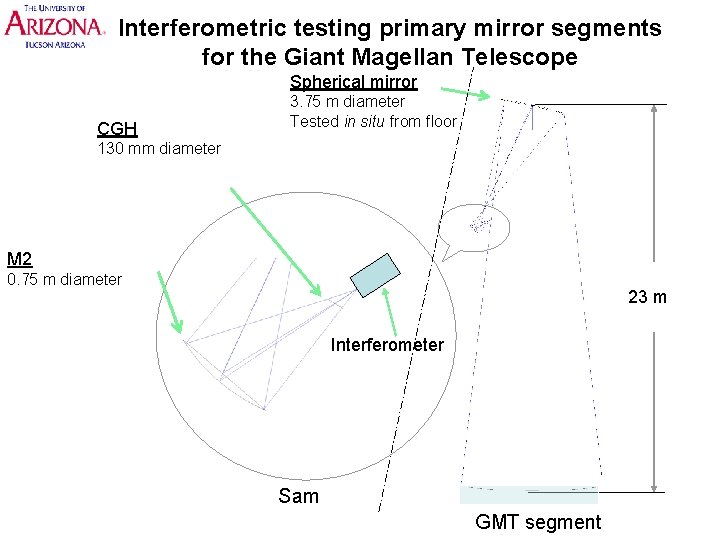
Interferometric testing primary mirror segments for the Giant Magellan Telescope Spherical mirror CGH 3. 75 m diameter Tested in situ from floor 130 mm diameter M 2 0. 75 m diameter 23 m Interferometer Sam GMT segment

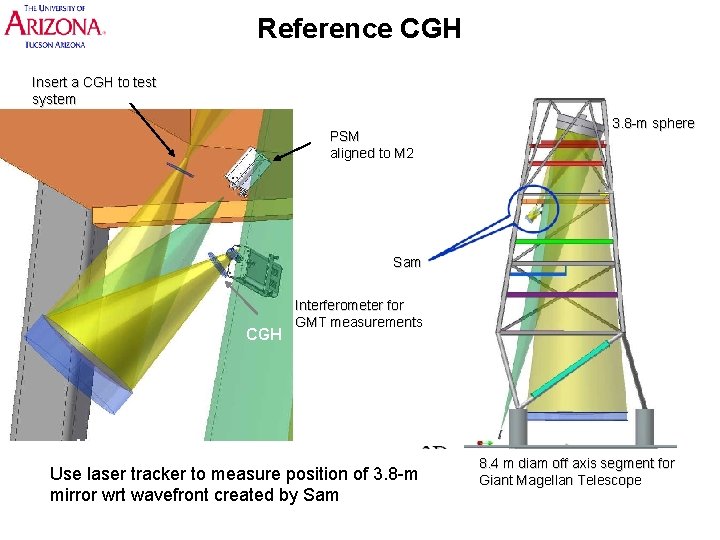
Reference CGH Insert a CGH to test system PSM aligned to M 2 3. 8 -m sphere Sam CGH Interferometer for GMT measurements M 2 Use laser tracker to measure position of 3. 8 -m mirror wrt wavefront created by Sam 8. 4 m diam off axis segment for Giant Magellan Telescope

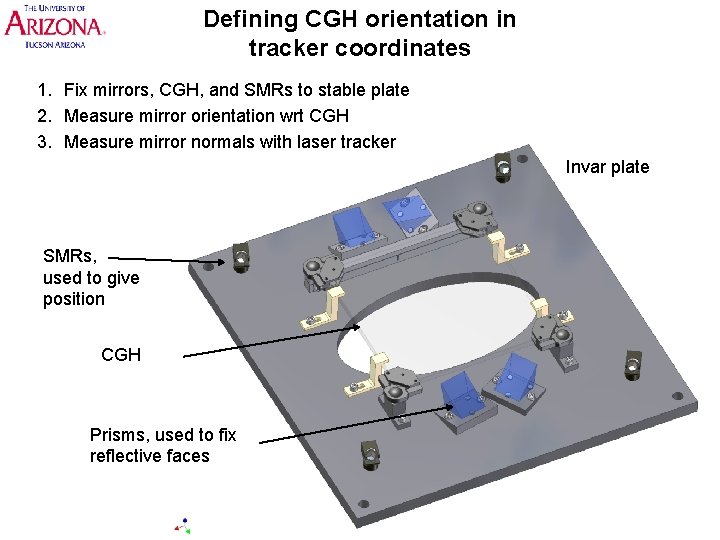
Defining CGH orientation in tracker coordinates 1. Fix mirrors, CGH, and SMRs to stable plate 2. Measure mirror orientation wrt CGH 3. Measure mirror normals with laser tracker Invar plate SMRs, used to give position CGH Prisms, used to fix reflective faces

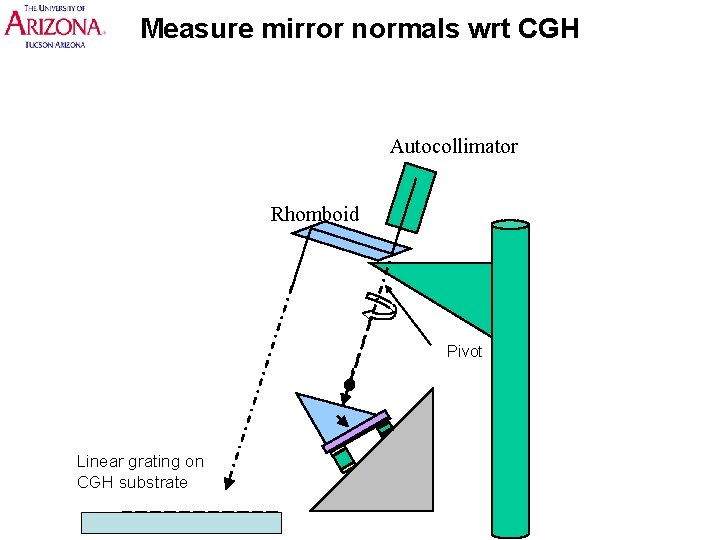
Measure mirror normals wrt CGH Autocollimator Rhomboid Pivot Linear grating on CGH substrate

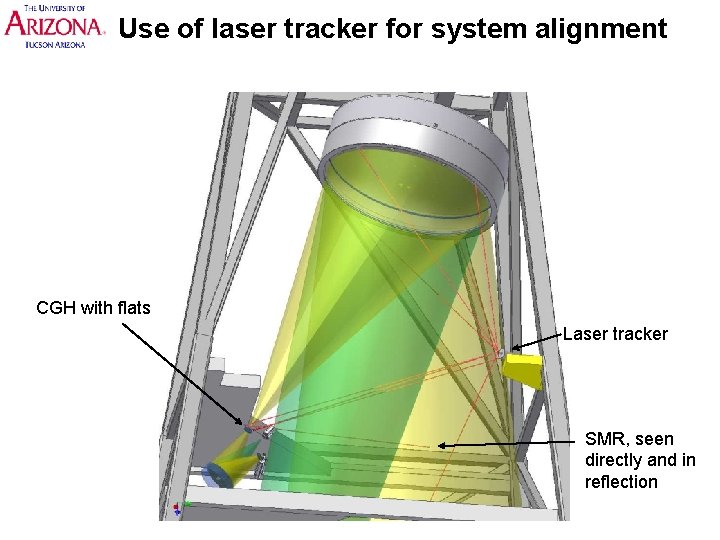
Use of laser tracker for system alignment CGH with flats Laser tracker SMR, seen directly and in reflection

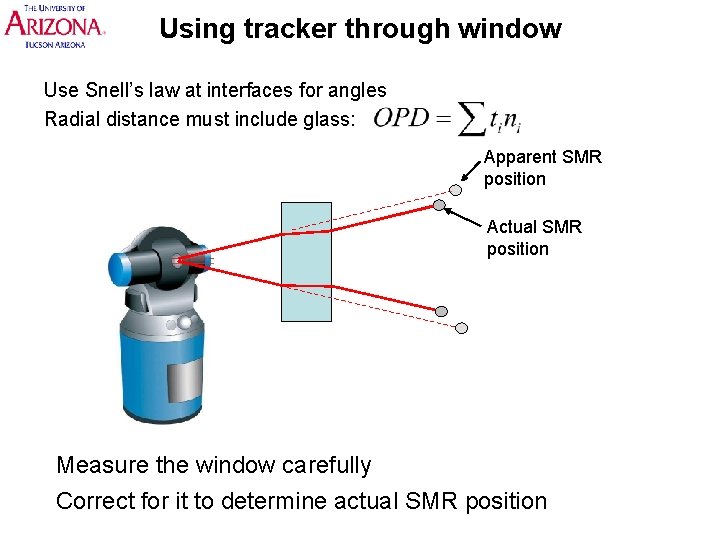
Using tracker through window Use Snell’s law at interfaces for angles Radial distance must include glass: Apparent SMR position Actual SMR position Measure the window carefully Correct for it to determine actual SMR position

Test of tracker looking through window • An SMR was measured directly at ~1 m • 1 cm thick window was inserted between the tracker and the SMR • The apparent SMR position was measured with the tracker • This was corrected for the refraction of the window • These tests showed agreement to 20 ppm, which is consistent with the noise levels of this test

Conclusion • The laser tracker is great for general purpose metrology • It has some special capabilities that make it especially useful for optical alignment – – Follows the light through fold mirrors Can be calibrated to very high accuracy Can be used for measuring angle as well as position Can be used to measure through a window