Unsymmetrical fault UNSYMMETRICAL CHAPTER 6 FAULTS EET 308

Unsymmetrical fault UNSYMMETRICAL CHAPTER 6 FAULTS EET 308 – POWER SYSTEM ANALYSIS MUHD HAFIZI IDRIS

UNDERSTAND THIS : - SINGLE LINE TO GROUND FAULT - LINE TO LINE FAULT - DOUBLE LINE TO GROUND FAULT Ability to analyze fault current in UNSYMMETRICAL Fault

SEQUENCE NETWORKS OF A LOADED GENERATOR Synchronous generator with neutral grounded through Impedance Zn. The generator is supplying three phase balanced load. The generator generates balanced three phase internal voltages represented by Ea, Eb and Ec.

Writing the terminal voltages; Substituting In = Ia + Ib + Ic and writing in matrix; In compact form;

Transform into their symmetrical components; Multiplying by A-1; EQUATION 1 Where;

Then we get; Since the generated emf is balanced, there is only positive sequence internal voltage; Substituting E 012 and Z 012 into EQUATION 1; IMPORTANT EQUATIONS! Where;

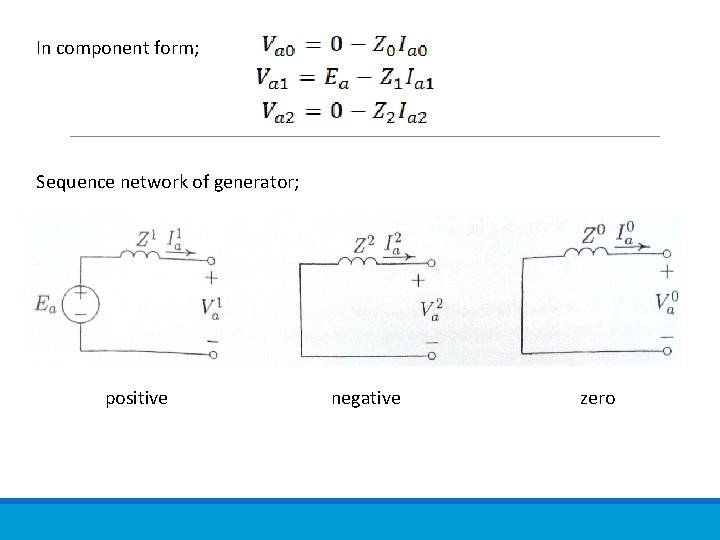
In component form; Sequence network of generator; positive negative zero

CONT. Important observations; ◦ The three sequences are independent. ◦ Only the positive sequence network has a voltage source. ◦ There is no voltage source in negative and zero sequence networks. ◦ The neutral of the system is the reference for the positive and negative sequence networks, but ground is the reference for the zero sequence network. The zero sequence current only can flow when there is connection between phase to ground to the neutral of the system.

TYPES OF UNSYMMETRICAL FAULTS q. Single Line To Ground Fault q. Line to Line Fault q. Double Line to Ground Fault A fault can have fault impedance value, Zf or zero fault impedance (bolted fault)

SINGLE LINE TO GROUND FAULT Assume generator on no load. Symmetrical components of currents. We get:

From; We get; Where ; Next;

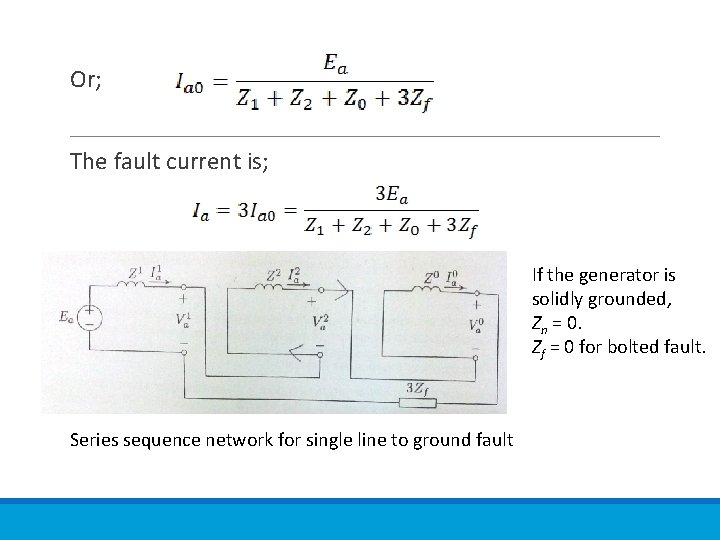
Or; The fault current is; If the generator is solidly grounded, Zn = 0. Zf = 0 for bolted fault. Series sequence network for single line to ground fault

LINE TO LINE FAULT Assume generator initially no load. Symmetrical components of currents; We get; EQUATION 2 And also;

EQUATION 3 Substituting only for Va 1 and Va 2 and noting Ia 2 = - Ia 1 for matrix below; We get;

Next, from EQUATION 3; From EQUATION 2; Thus;

The phase currents are; The fault current is;

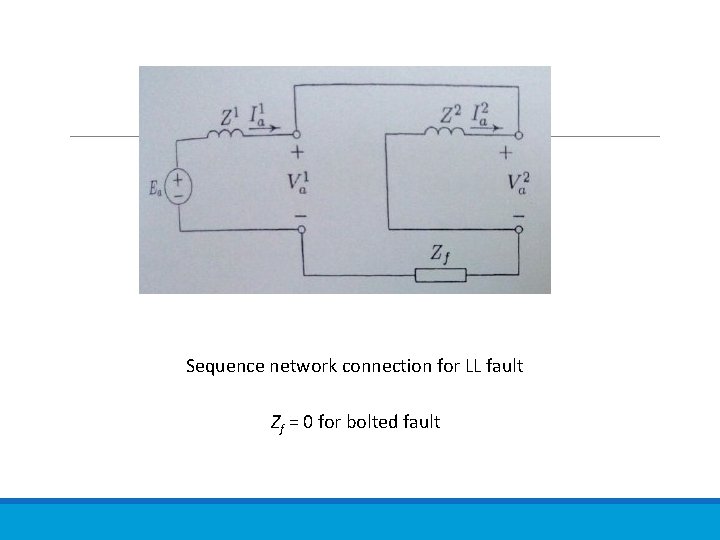
Sequence network connection for LL fault Zf = 0 for bolted fault

EXAMPLE 1

EXAMPLE 2

DOUBLE LINE TO GROUND FAULT Fault in this case is assumed to occur on phases b and c through an impedance Zf to the ground. Generator assumed initially on no-load.

The boundary conditions at fault point: EQUATION 4 EQUATION 5 The phase voltages Vb and Vc: EQUATION 6 Since Vb = Vc, we note that: EQUATION 7

Substituting for the symmetrical components of currents in EQUATION 4: EQUATION 8 From EQUATION 5: Substituting into EQUATION 8: Substituting for Vb using EQUATION 6 by equating Va 1 = Va 2 : EQUATION 9

From the symmetrical components of voltage for generator; Substituting the symmetrical components of voltage into EQUATION 9, we get; From symmetrical components of voltage;

Substituting Ia 0 and Ia 2 into EQUATION 5 and solving for Ia 1, we get; To get the phase current; The fault current;

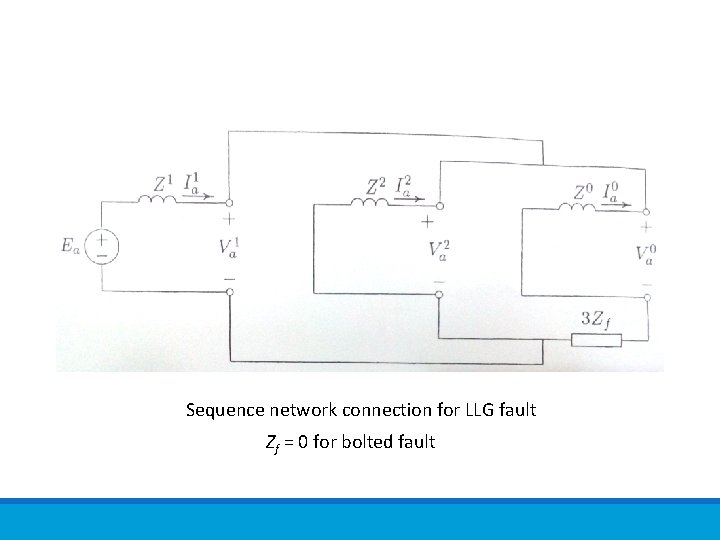
Sequence network connection for LLG fault Zf = 0 for bolted fault

UNBALANCED FAULT ANALYSIS USING BUS IMPEDANCE MATRIX

INTRO. When the network is balanced, the symmetrical components impedances are diagonal, so it is possible to calculate Zbus separately for zero, positive and negative sequence networks. For a fault at bus k, the diagonal element in the k axis of the bus impedance matrix Zbus is the Thevenin impedance to the point of fault. For unbalanced faults, the impedance matrix for each sequence network is obtained separately. The sequence impedance Z 0 kk, Z 1 kk and Z 2 kk are connected together as we already discussed in previous slides for different types of unsymmetrical faults. Here, the subscript a is left out and the symmetrical components are understood to refer to phase a.

SLG FAULT USING Zbus SLG fault requires that positive, negative and zero sequence networks for phase a be placed in series in order to compute the zero sequence fault current as discussed previously. Thus for a SLG fault at bus k, the symmetrical components of fault current are; Where Z 1 kk , Z 2 kk and Z 0 kk are the diagonal elements in the k axis of the corresponding symmetrical sequence bus impedance matrix and Vk(0) is the prefault voltage at bus k. The fault phase current is;

LL FAULT USING Zbus As we already discussed previously, for LL fault, the positive and negative sequence networks are placed in opposition. The symmetrical components of fault currents are; The fault phase current then is obtained using;

DLG FAULT USING Zbus As we already discussed previously, for DLG fault, the positive sequence network is placed in series with the parallel combination of the negative and zero sequence networks. The symmetrical components of faults current are; The phase currents are obtained from; The fault current is;

BUS VOLTAGES AND LINE CURRENTS DURING FAULTS To get the symmetrical components of the ith bus voltages during fault, we use back the sequence components of the terminal voltages of the generator that we already discussed previously. So, we have; Where; Prefault phase voltage at bus i The phase voltages during fault are;

The symmetrical components of current in line i to j given by; Where z 0 ij, z 1 ij and z 2 ij are the zero, positive and negative sequence components of the actual line impedance between bus i and j. The phase fault currents in line i to j during fault are;