Unsupervised Forward Selection A data reduction algorithm for

Unsupervised Forward Selection A data reduction algorithm for use with very large data sets David Whitley†, Martyn Ford† and David Livingstone†‡ †Centre for Molecular Design, University of Portsmouth †‡Chem. Quest

Outline • • • Variable selection issues Pre-processing strategy Dealing with multicollinearity Unsupervised forward selection Model selection strategy Applications

Variable Selection Issues • Relevance – statistically significant correlation with response – non-small variance • Redundancy – linear dependence – some variables have no unique information • Multicollinearity – near linear dependence – some variables have little unique information

Pre-processing Strategy • Identify variables with a significant correlation with the response • Remove variables with small variance • Remove variables with no unique information • Identify a set of variables on which to construct a model

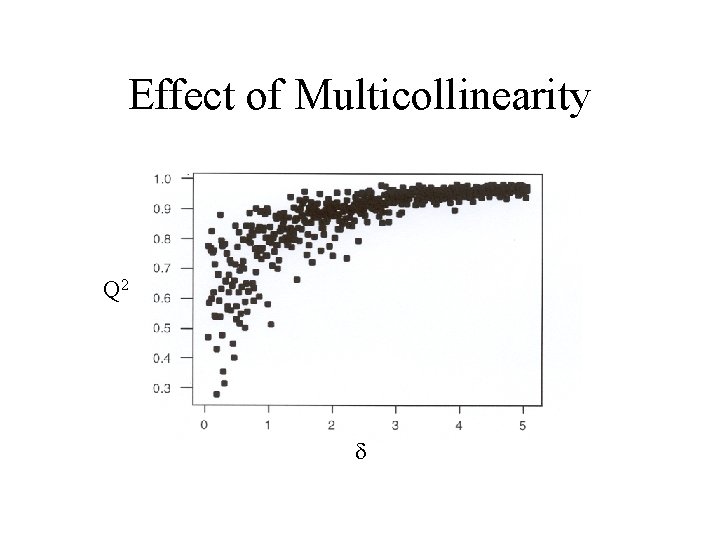
Effect of Multicollinearity Build regression models of the form where and x 1 - x 4 , y, zi and ei are random N(0, 1) Increasing reduces the collinearity between x 5 and x 1

Effect of Multicollinearity Q 2

Dealing with Multicollinearity • Examine pair-wise correlations between variables, and remove one from each pair with high correlation • Corchop (Livingstone & Rahr, 1989) aims to remove the smallest number of variables while breaking the largest number of pair-wise collinearities

Unsupervised Forward Selection 1 Select the first two variables with the smallest pairwise correlation coefficient 2 Reject variables whose pair-wise correlation coefficient with the selected columns exceeds rsqmax 3 Select the next variable to have the smallest squared multiple correlation coefficient with those previously selected 4 Reject variables with squared multiple correlation coefficients greater than rsqmax 5 Repeat 3 - 4 until all variables are selected or rejected

Continuum Regression • A regression procedure with the generalized criterion function • Varying the continuous parameter 0 1. 5 adjusts the balance between the covariance of the response with the descriptors and the variance of the descriptors, so that – = 0 is equivalent to ordinary least squares – = 0. 5 is equivalent to partial least squares – = 1. 0 is equivalent to principal components regression

Model Selection Strategy • For = 0. 0, 0. 1, …, 1. 5 build a CR model for the set of variables selected by UFS with rsqmax = 0. 1, 0. 2, …, 0. 99 • Select the model with rsqmax and maximizing Q 2 (leave-one-out cross-validated R 2) – Apply n-fold cross-validation to check predictive ability – Apply a randomization test (1000 permutations of the response scores) to guard against chance correlation

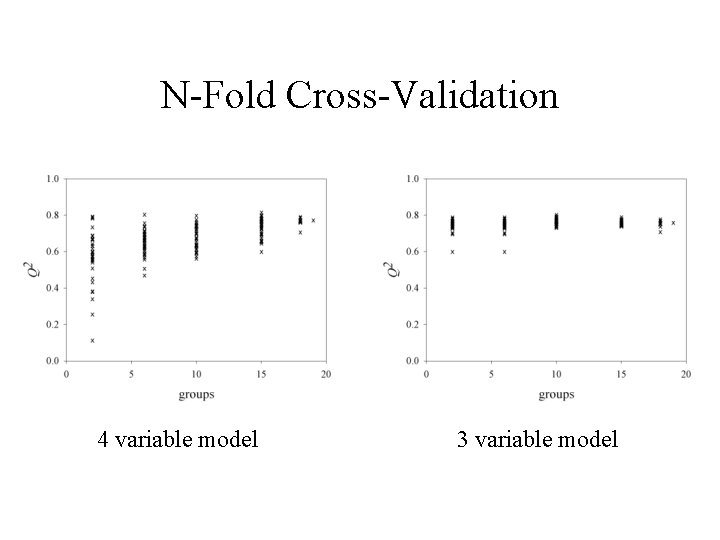
Pyrethroid Data Set • 70 physicochemical descriptors to predict killing activity (KA) of 19 pyrethroid insecticides • Only 6 descriptors are correlated with KA at the 5% level • Optimal models – 4 -variable, 2 -component model with R 2 = 0. 775, Q 2 = 0. 773 obtained when rsqmax = 0. 7, = 1. 2 – 3 -variable, 1 -component model with R 2 = 0. 81, Q 2 = 0. 76 obtained when rsqmax = 0. 6, = 0. 2

Optimal Model I • Standard errors are bootstrap estimates based on 5000 bootstraps • Randomization test tail probabilities below 0. 0003 for fit and 0. 0071 for prediction

Optimal Model II • Standard errors are bootstrap estimates based on 5000 bootstraps • Randomization test tail probabilities below 0. 0001 for fit and 0. 0052 for prediction

N-Fold Cross-Validation 4 variable model 3 variable model

Feature Recognition • Important explanatory variables may not be selected for inclusion in the model – force some variables in, then continue UFS algorithm • The component loadings for the original variables can be examined to identify variables highly correlated with the components in the model

Loadings for the 1 -component pyrethroid model with tail probability < 0. 01

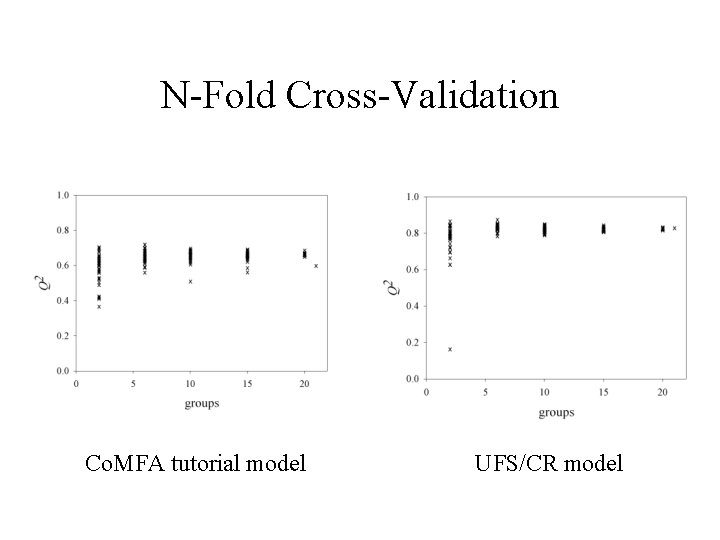
Steroid Data Set • 21 steroid compounds from SYBYL Co. MFA tutorial to model binding affinity to human TBG • Initial data set has 1248 variables with values below 30 kcal/mol • Removed 858 variables not significantly correlated with response (5% level) • Removed 367 variables with variance below 1. 0 kcal/mol • Leaving 23 variables to be processed by UFS/CR

Optimal models • UFS/CR produces a 3 -variable, 1 -component model with R 2 = 0. 85, Q 2 = 0. 83 at rsqmax = 0. 3, = 0. 3 • Co. MFA tutorial produces a 5 -component model with R 2 = 0. 98, Q 2 = 0. 6

N-Fold Cross-Validation Co. MFA tutorial model UFS/CR model

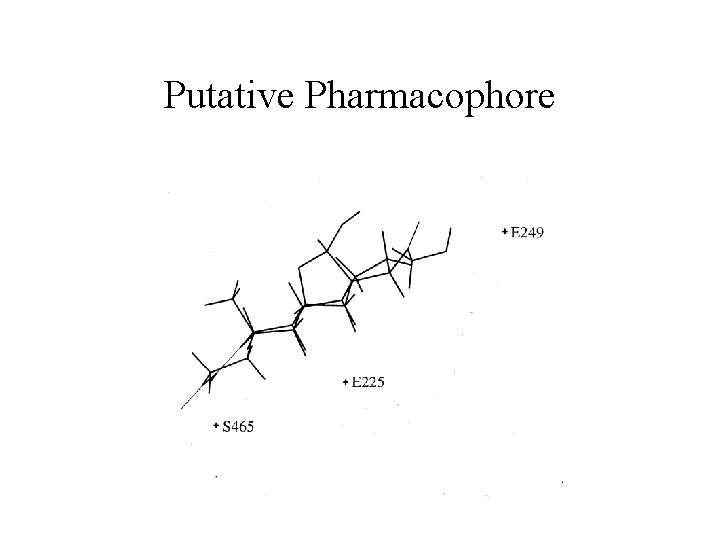
Putative Pharmacophore

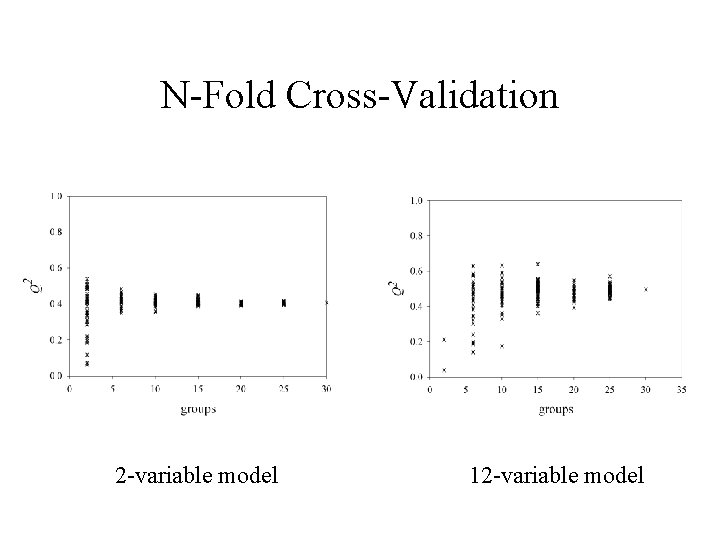
Selwood Data Set • 53 descriptors to predict biological activity of 31 antifilarial antimycin analogues • 12 descriptors are correlated with the response variable at the 5% level • Optimal models – 2 -variable, 1 -component model with R 2 = 0. 42, Q 2 = 0. 41 obtained when rsqmax = 0. 1, = 1. 0 – 12 -variable, 1 -component model with R 2 = 0. 85, Q 2 = 0. 5 obtained when rsqmax = 0. 99, = 0. 0 (omitting compound M 6)

N-Fold Cross-Validation 2 -variable model 12 -variable model

Summary • Multicollinearity is a potential cause of poor predictive power in regression. • The UFS algorithm eliminates redundancy and reduces multicollinearity, thus improving the chances of obtaining robust, low-dimensional regression models. • Chance correlation can be addressed by eliminating variables that are uncorrelated with the response.

Summary • UFS can be used to adjust the balance between reducing multicollinearity and including relevant information. • Case studies show that leave-one-out crossvalidation should be supplemented by n-fold cross -validation, in order to obtain accurate and precise estimates of predictive ability (Q 2).

Acknowledgements BBSRC Cooperation with Industry Project: Improved Mathematical Methods for Drug Design • • Astra Zeneca Glaxo. Smith. Kline MSI Unilever

Reference D. C. Whitley, M. G. Ford and D. J. Livingstone Unsupervised forward selection: a method for eliminating redundant variables. J. Chem. Inf. Comp. Sci. , 2000, 40, 1160 -1168. UFS software available from: http: //www. cmd. port. ac. uk CR is a component of Paragon (available summer 2001)