Unsaturated Flow Governing Equations Richards Equation 1 Richards

1. Richards Eq: General Form (A) Apply mass conservation principle to REV Mass Inflow

1. Richards Eq: General Form • Mass outflow rate through face EFGH is •

1. Richards Eq: General Form • Similarly, net inflow rate thru face DCGH is

1. Richards Eq: General Form • The total net inflow rate through all faces

1. Richards Eq: General Form • Equating net inflow rate and time rate of

1. Richards Eq: General Form • If ρw varies neither spatially nor temporally, (1)

1. Richards Eq: General Form (B) Apply Darcy’s law to Eq 2 = (3)

1. Richards Eq: General Form • Substituting the above equations into Eq 3 leads

1. Richards Eq: General Form $ Eq 4 is the 3 -d Richards equation—the

2. Simplified Cases (A) If Lz (gravity gradient) negligible compared to the strong matric

2. Simplified Cases (B) 2 -d horizontal flow: (4) becomes (6) For 1 -d

2. Simplified Cases (C) Vertical flow: if lateral flow elements negligible, (4) becomes Rewrite

2. Simplified Cases • Use chain rule of differentiation on term • Define as

2. Simplified Cases • Substitute the equations into Richards’ Eq, we have

2. Simplified Cases • Define as soil water diffusivity, we have Richards’ Eq in

2. Simplified Cases • Now, use the chain rule of differentiation to the relationship

2. Simplified Cases • Generally, if flow is neither vertical nor horizontal, we have

2. Simplified Cases • Consider sink/source terms (e. g. plant uptake), we have (13)

Slides: 27

Download presentation

Unsaturated Flow Governing Equations —Richards’ Equation

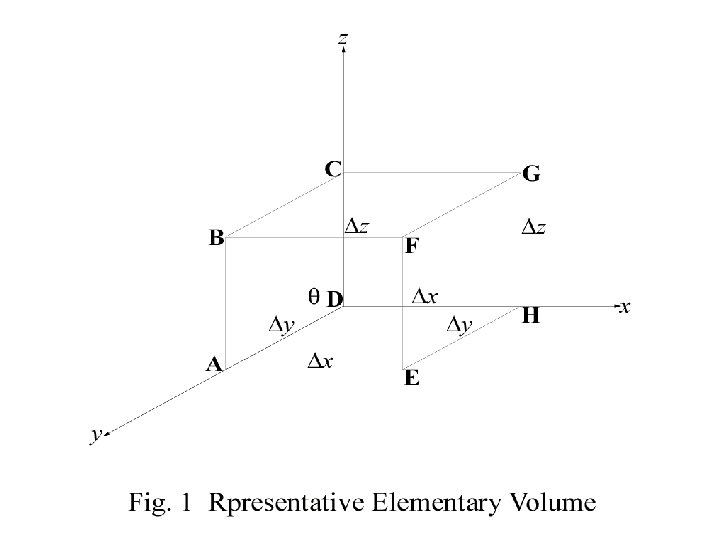
1. Richards Eq: General Form (A) Apply mass conservation principle to REV Mass Inflow Rate − Mass Outflow Rate = Change in Mass Storage with Time For a REV with volume mass inflow rate through face ABCD is

1. Richards Eq: General Form • Mass outflow rate through face EFGH is • The net inflow rate is thus

1. Richards Eq: General Form • Similarly, net inflow rate thru face DCGH is • and net inflow rate thru face ADHE is

1. Richards Eq: General Form • The total net inflow rate through all faces is then • The change in mass storage is θ: volumetric water content [L 3 L− 3]

1. Richards Eq: General Form • Equating net inflow rate and time rate of change in mass storage, and dividing both sides by leads to = (1) • In fact, (1) can be obtained directly from

1. Richards Eq: General Form • If ρw varies neither spatially nor temporally, (1) becomes = (2)

1. Richards Eq: General Form (B) Apply Darcy’s law to Eq 2 = (3) (physics or Lecture 12 notes) is metric potential, h is total potential

1. Richards Eq: General Form • Substituting the above equations into Eq 3 leads to = (4)

1. Richards Eq: General Form $ Eq 4 is the 3 -d Richards equation—the basic theoretical framework for unsaturated flow in a homogeneous, isotropic porous medium $ Eq 4 is not applicable to macropore flows $ Eq 4 (Darcy’s law for unsaturated flow) does not address hysteresis effects $ Both K and ψ are a function of θ, making Richards equation non-linear and hard to solve

2. Simplified Cases (A) If Lz (gravity gradient) negligible compared to the strong matric potential L, (4) becomes (5)

2. Simplified Cases (B) 2 -d horizontal flow: (4) becomes (6) For 1 -d horizontal flow (6) becomes (7)

2. Simplified Cases (C) Vertical flow: if lateral flow elements negligible, (4) becomes Rewrite it as (8)

2. Simplified Cases • Use chain rule of differentiation on term • Define as water capacity, we have (9)

2. Simplified Cases • Substitute the equations into Richards’ Eq, we have

2. Simplified Cases • Define as soil water diffusivity, we have Richards’ Eq in water content form (10)

2. Simplified Cases • Now, use the chain rule of differentiation to the relationship of water content and water potential • We obtain Richards’ Eq in water potential form (11)

2. Simplified Cases • Generally, if flow is neither vertical nor horizontal, we have (12) • Where is the angle between flow direction and vertical axis; =90 o, horizontal flow, Eq 6; =0 o, vertical flow, Eq 8

2. Simplified Cases • Consider sink/source terms (e. g. plant uptake), we have (13) • Where S is the sink/source term (e. g. used to represent plant uptake in HYDRUS 1 D/2 D)