University of Science and Technology Faculty of Computer
















































- Slides: 68

University of Science and Technology Faculty of Computer Science and Information Technology Computer Science –Department 4 th- Year Computer Graphics Chapter(2) Mathematics For Computer Graphics

Overview • Coordinates Systems – Types (2 D , 3 D) , transforms from one to another. • Points, Vectors – Representations , operations, examples • Linear Algebra , Matrices – definitions, operations, solution of linear equations , examples. – Using matrices in geometric transformations. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 2

n. D Space: n (typically) n : number of dimensions Examples: • 1 D space: time, along a line or curve • 2 D space: plane, sphere • 3 D space: the world we live in • 4 D space: 3 D + time Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 3

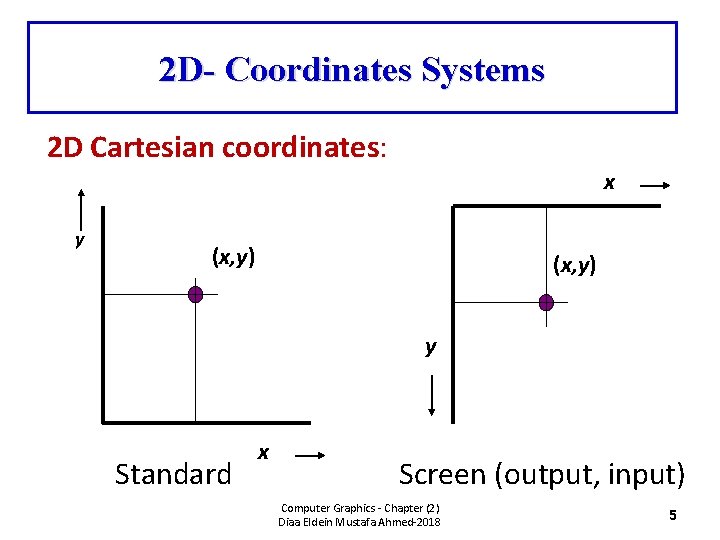
2 D- Coordinates Systems • In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 4

2 D- Coordinates Systems 2 D Cartesian coordinates: x y (x, y) y Standard x Screen (output, input) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 5

2 D- Coordinates Systems Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 6

2 D- Coordinates Systems 2 D-Polar Coordinates y (x, y) r x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 7

2 D-Coordinates Systems Transforms from Polar to Cartesian y (x, y) 4 60 x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 8

2 D- Coordinates Systems Transforms from Cartesian to Polar y (3, 4) r x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 9

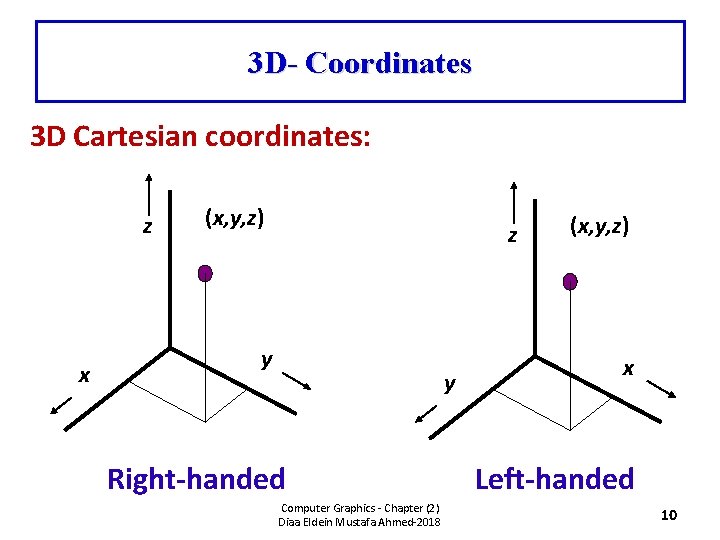
3 D- Coordinates 3 D Cartesian coordinates: z x (x, y, z) z y y Right-handed Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 (x, y, z) x Left-handed 10

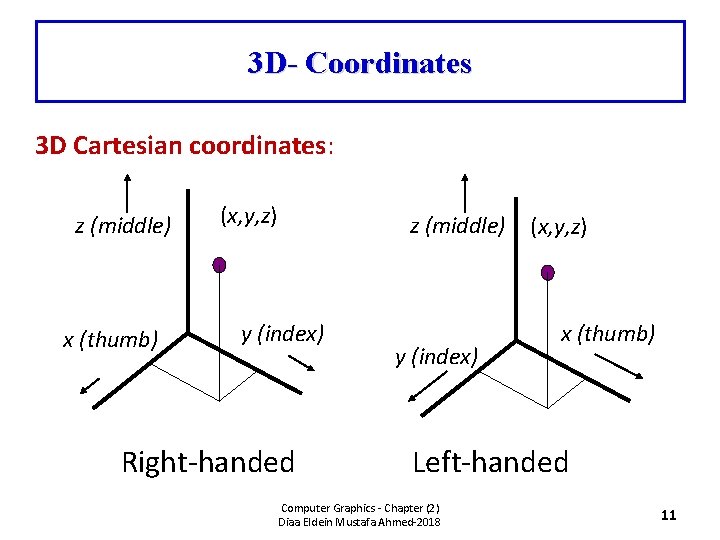
3 D- Coordinates 3 D Cartesian coordinates: z (middle) x (thumb) (x, y, z) z (middle) y (index) Right-handed y (index) (x, y, z) x (thumb) Left-handed Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 11

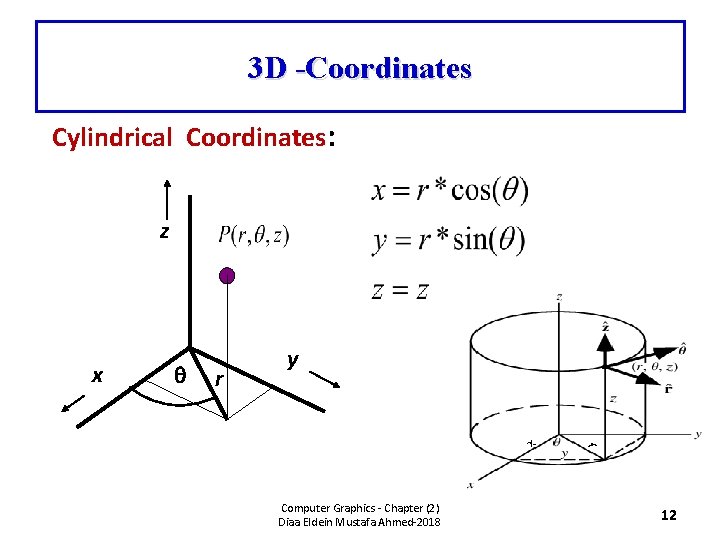
3 D -Coordinates Cylindrical Coordinates: z x r y Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 12

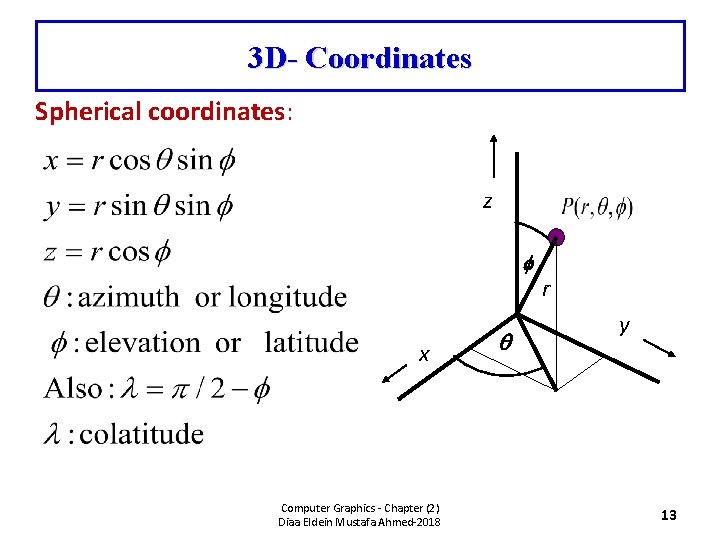
3 D- Coordinates Spherical coordinates: z f x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 r y 13

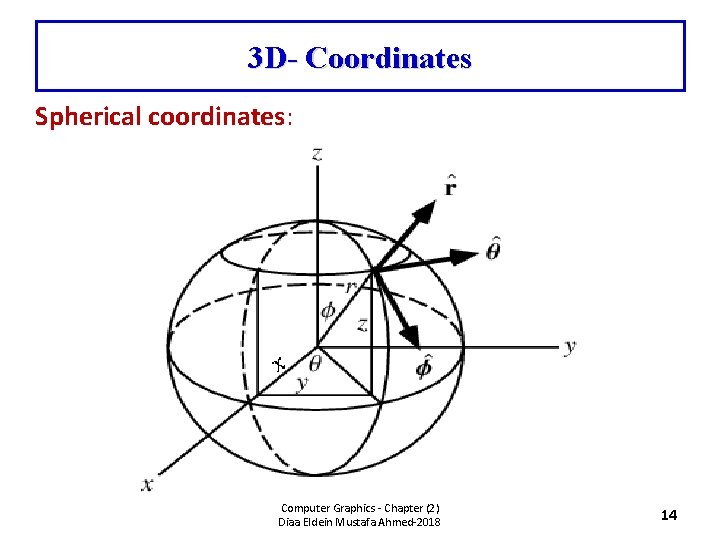
3 D- Coordinates Spherical coordinates: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 14

Points • • Point: position in n. D space. Notation: P (H&B), also P, p, p en p (x, y), (x 1, x 2) , (Px, Py) in 2 D- Cartesian (x, y, z), also (x 1 , x 2 , x 3), (Px , Py , Pz), in 3 D-Cartesian P(r, ) in 2 D-Polar P (r, , z) in 3 D- Cylindrical ( r, , ) in 3 D- Spherical Reference in Graphic Systems : point represented by pixel with : (1) Integer position (x, y), relative to the position of the screen-coordinate origin and (2) Color x: get. Pixel (x, y, color); Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 15

Vectors • Vector: – “arrow” – multiple interpretations (displacement, velocity, force, …) – has a magnitude and direction – has no position • Notation: V (H&B), also V, v, v en v • (Vx, Vy, Vz) (H&B), also (x, y, z), (x 1, x 2, x 3) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 16

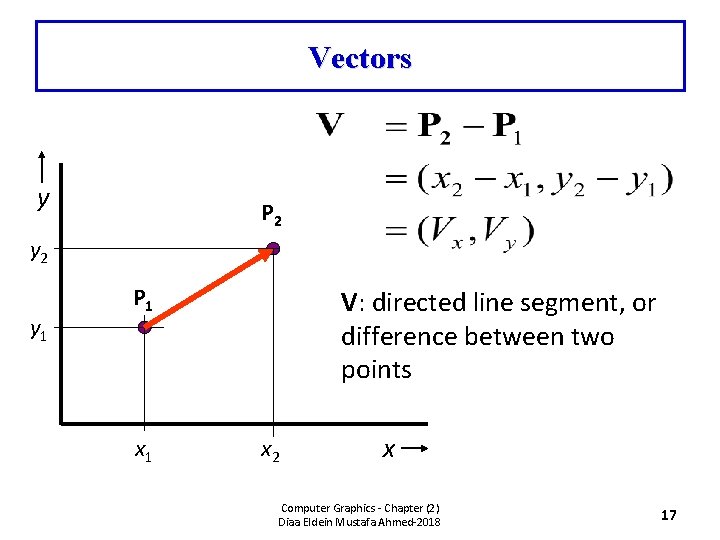
Vectors y P 2 y 1 P 1 x 1 V: directed line segment, or difference between two points x 2 x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 17

Vectors Length of a vector: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 18

Vectors Direction of a vector: Direction angles. z g b Unit vector V : y x a Magnitude info is removed, direction is kept. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 19

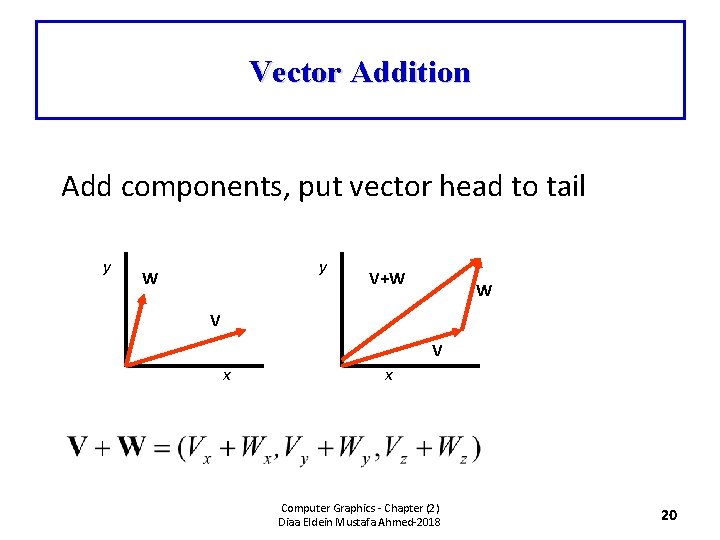
Vector Addition Add components, put vector head to tail y y W V+W W V V x x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 20

Scalar Multiplication of Vector Multiplication components with scalar s y y 2 V V x x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 21

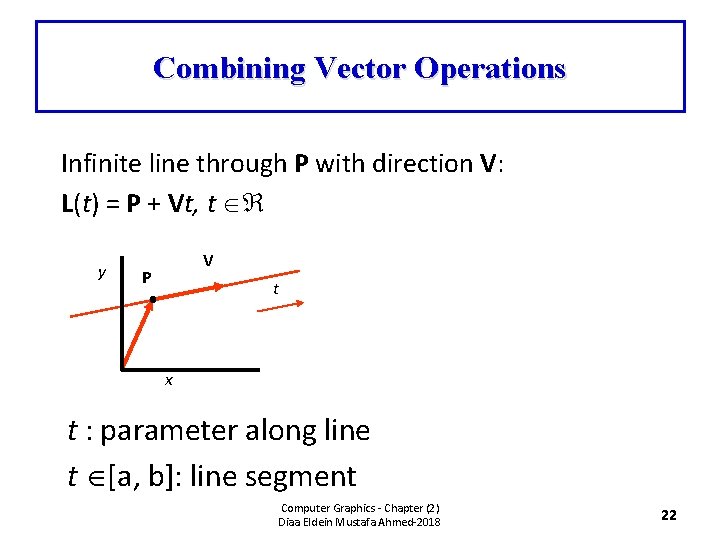
Combining Vector Operations Infinite line through P with direction V: L(t) = P + Vt, t y V P t x t : parameter along line t [a, b]: line segment Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 22

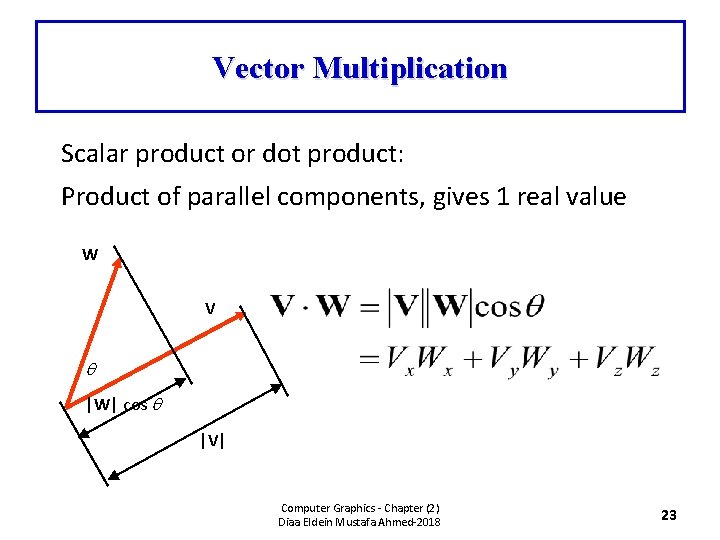
Vector Multiplication Scalar product or dot product: Product of parallel components, gives 1 real value W V |W| cos |V| Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 23

Vector Multiplication Scalar product: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 24

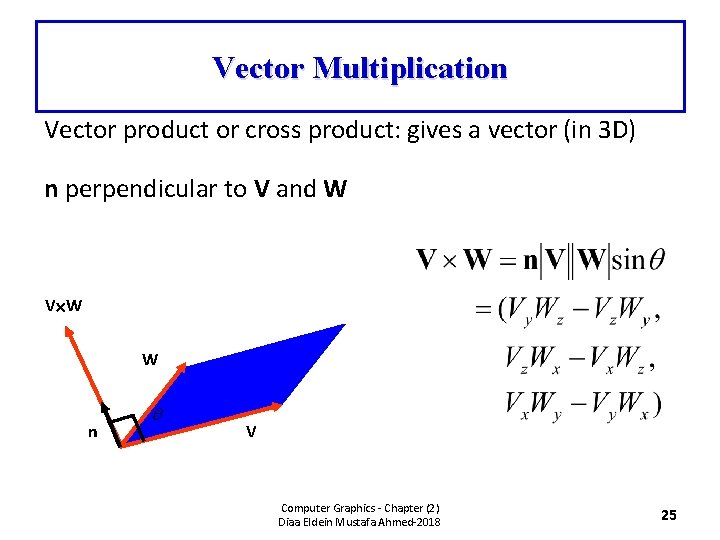
Vector Multiplication Vector product or cross product: gives a vector (in 3 D) n perpendicular to V and W V W W n V Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 25

Vector multiplication Scalar product: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 26

Vector Multiplication Scalar product: • scalar • Test if vectors are perpendicular • cos • project, … Vector product: • vector • Get a vector perpendicular to two given vectors • sin • surface area, … Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 27

Example (1) • Given a point P. • Requested: Reflect a point Q with respect to P. Q W y P W x Q’ W=P–Q Q’ = Q + 2 W = 2 P – Q or: = P + (P – Q ) We don’t need coordinates! Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 28

Example (1) • Given a point P. • Requested: Reflect a point Q with respect to P. Q P Q’ Alternative P is halfway Q and Q’: P = (Q + Q’)/2 2 P = Q + Q’ Q’ = 2 P – Q Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 29

Example (2) • Given a line L: L(t) = P + Vt. • Requested: Reflect a point Q with respect to L. Q W y V P W t L(t) Q’ We know: Q’ = Q + 2 W W = L(t) – Q W. V = 0 x Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 30

Example (2) We know: L(t) = P + Vt Q’ = Q + 2 W W = L(t) – Q W. V = 0 Substitute to get t: (L(t) – Q). V = 0 (P + Vt – Q). V = 0 V. V t + (P – Q). V = 0 t = ((Q – P). V) / (V. V) Then: Q’ = Q + 2 (P + Vt – Q) = 2 P – Q + V((Q – P). V / V. V) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 31

Steps To Be Made • Write down what you know • Eliminate, substitute, etc. to get he result • Check the result – Does it make sense? – Is there a simpler derivation? Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 32

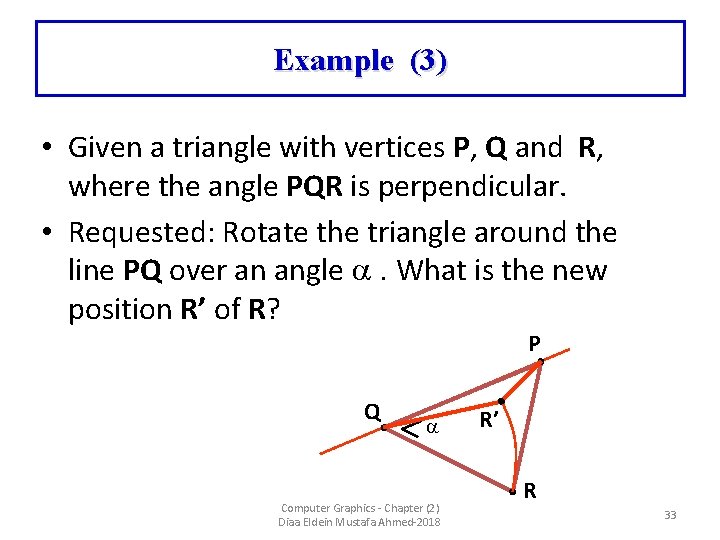
Example (3) • Given a triangle with vertices P, Q and R, where the angle PQR is perpendicular. • Requested: Rotate the triangle around the line PQ over an angle . What is the new position R’ of R? P Q Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 R’ R 33

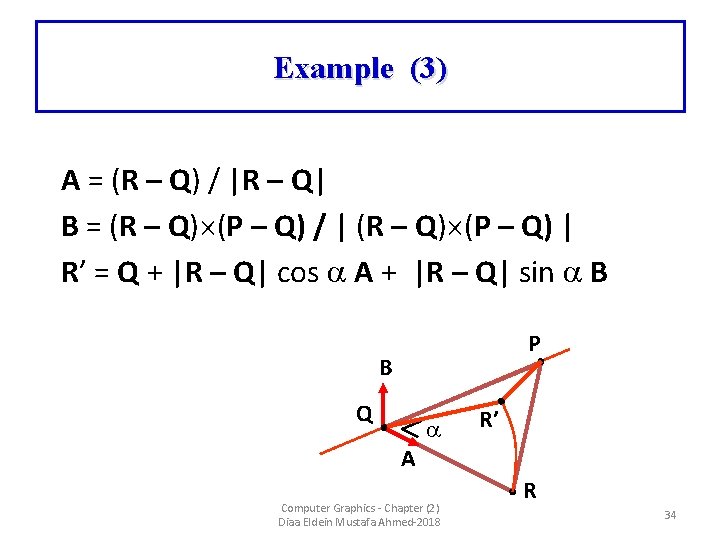
Example (3) A = (R – Q) / |R – Q| B = (R – Q) (P – Q) / | (R – Q) (P – Q) | R’ = Q + |R – Q| cos A + |R – Q| sin B P B Q R’ A Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 R 34

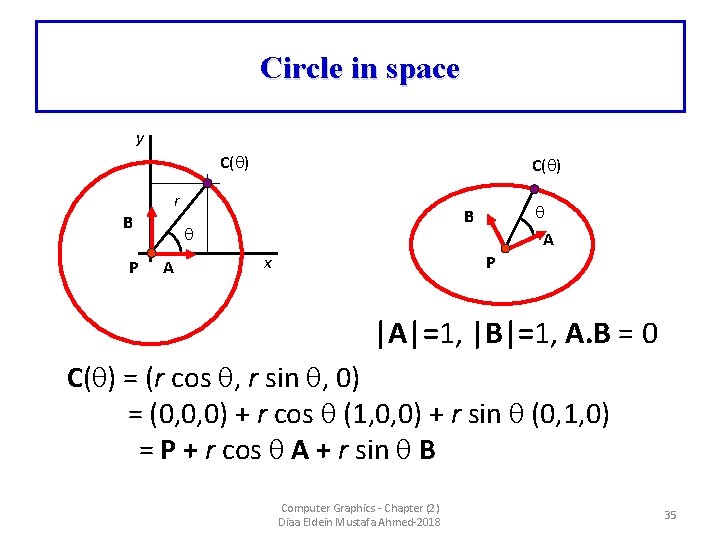
Circle in space y C( ) r B P A B A P x |A|=1, |B|=1, A. B = 0 C( ) = (r cos , r sin , 0) = (0, 0, 0) + r cos (1, 0, 0) + r sin (0, 1, 0) = P + r cos A + r sin B Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 35

Use: • Scalar product, cross product • coordinate independent definitions • vector algebra Don’t use: • arccos, arcsin • y = f(x) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 36

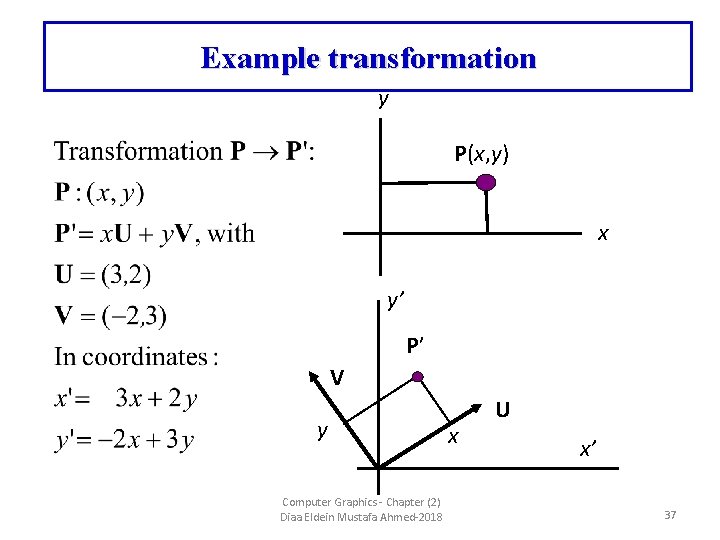
Example transformation y P(x, y) x y’ P’ V y Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 x U x’ 37

Linear Algebra System of linear equations: Such systems occur in many, many applications. They are studied in Linear Algebra. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 38

Linear Algebra System of linear equations: Typical questions: - Given u, v, w, what are x, y, z? - Can we find a unique solution? Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 39

Linear Algebra System of linear equations: Crucial in computer graphics: - Transforming geometric objects - Change of coordinates Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 40

What is a matrix? Matrix: - Mathematical objects with operations Matrix in computer graphics: - Defines a coordinate frame - Defines a transformation - Handy tool for manipulating transformations Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 41

Matrix: rectangular array of elements Element: quantity (value, expression, function, …) Examples: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 42

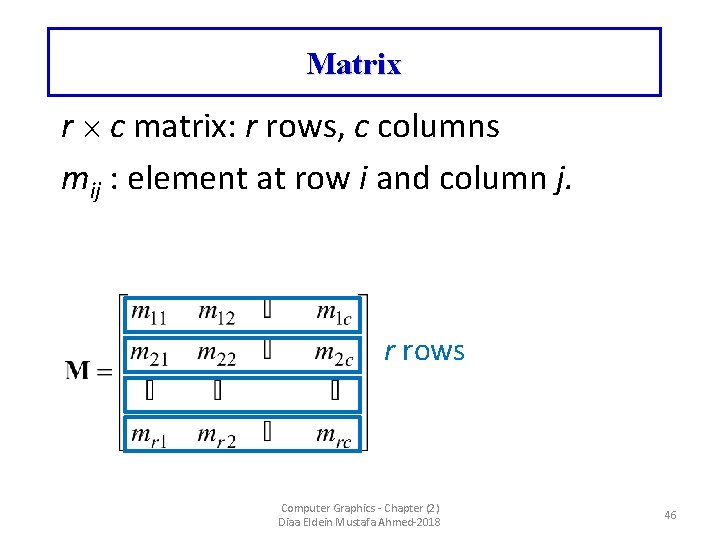
Matrix r c matrix: r rows, c columns mij : element at row i and column j. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 43

Matrix r c matrix: r rows, c columns mij : element at row i and column j. r c elements Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 44

Matrix r c matrix: r rows, c columns mij : element at row i and column j. c columns Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 45

Matrix r c matrix: r rows, c columns mij : element at row i and column j. r rows Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 46

Matrix Column vector: matrix with c =1 Row vector: matrix with r =1 Scalar: matrix with r=1 and c=1 Used for vectors (and points) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 47

Matrix as collection of column vectors: W Matrix contains an axis-frame: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 V U 48

Operations On Matrices • Multiplication with scalar – simple • Addition – simple • Matrix-matrix multiplication – More difficult, but the most important Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 49

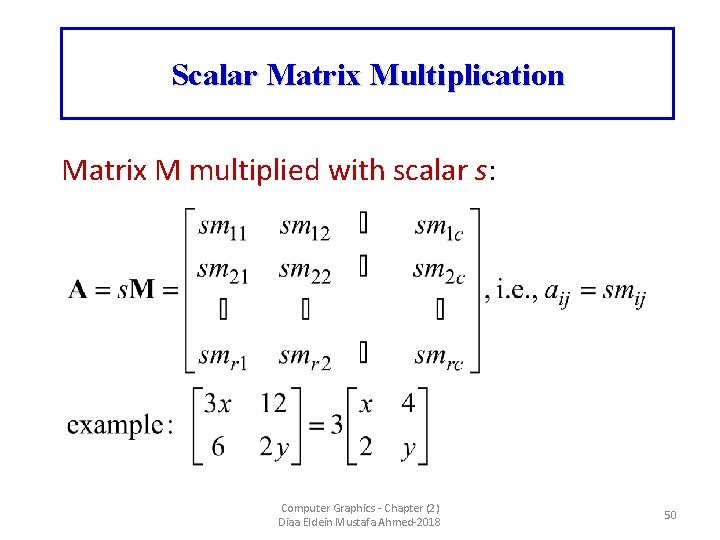
Scalar Matrix Multiplication Matrix M multiplied with scalar s: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 50

Scalar Matrix Addition Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 51

Scalar Matrix addition • Just add elements pairwise • A and B must have the same number of rows and columns • Generalization of vector and scalar addition Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 H&B A-5 52

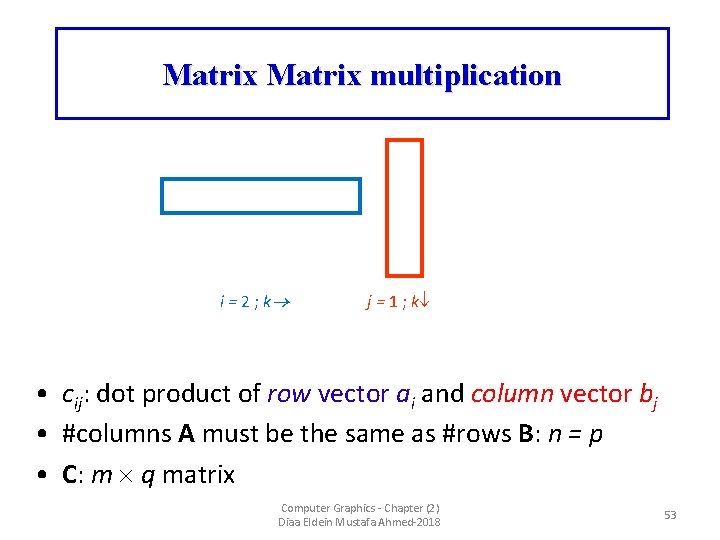
Matrix multiplication i = 2 ; k j = 1 ; k • cij: dot product of row vector ai and column vector bj • #columns A must be the same as #rows B: n = p • C: m q matrix Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 53

Matrix multiplication Example: i=3 j=2 i=3, j=2 Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 54

Matrix multiplication Example: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 55

Matrix multiplication Example: Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 56

Matrix multiplication Example: AB BA Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 57

Matrix Multiplication • AB BA Matrix multiplication is not commutative! Order matters! • A(B+C) = AB+AC Matrix multiplication is distributive Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 58

Example transformation sequence (coordinate version) Unclear! Error-prone! Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 59

Example transformation sequence (matrix vector version) Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 60

Example transformation sequence (compact matrix vector version) Matrix vector notation allows for compactness and genericity! Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 61

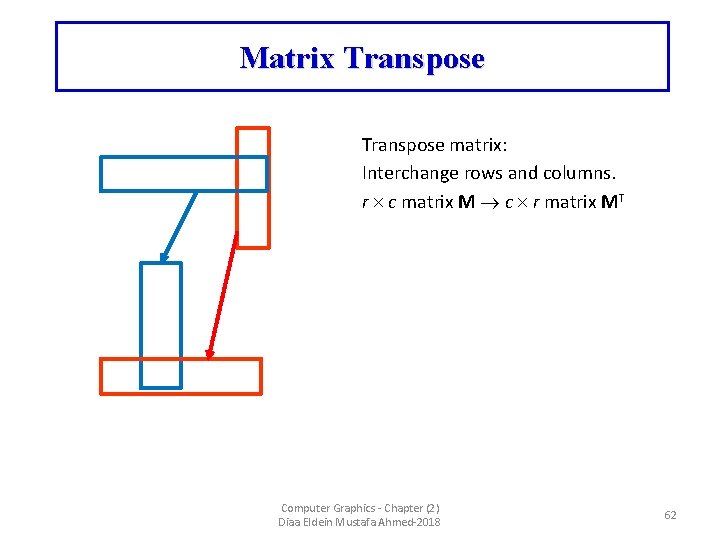
Matrix Transpose matrix: Interchange rows and columns. r c matrix M c r matrix MT Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 62

Matrix Inverse Simple algebra puzzle. Let ax = b. What is x? Linear algebra puzzle. Let MU = V. What is U? H&B A-5 Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 63

Matrix Inverse Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 64

Matrix Inverse examples Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 65

Matrix Inverse examples Does not exist, cannot be inverted. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 66

Matrix Inverse - Does not always exist - In general: if determinant = | M | = 0, matrix cannot be inverted - Inverse for n = 1 and n = 2: easy - Inverse for higher n: use library function - Important special case: orthonormal matrix. Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 67

Thank You End Computer Graphics - Chapter (2) Diaa Eldein Mustafa Ahmed-2018 68