University of British Columbia CPSC 314 Computer Graphics

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2005 Tamara Munzner Lighting and Shading Week 4, Fri Jan 28 n http: //www. ugrad. cs. ubc. ca/~cs 314/Vjan 200 5

Reading (today, Mon, Wed) n FCG n n Chapter 8 RB n Chapter Lighting 2

Correction from last time n row vectors not column vectors might have been confusing n but they’re mathematically equivalent 3

Perspective Warp n n n matrix formulation (with column vectors) preserves relative depth (third coordinate) what does mean?

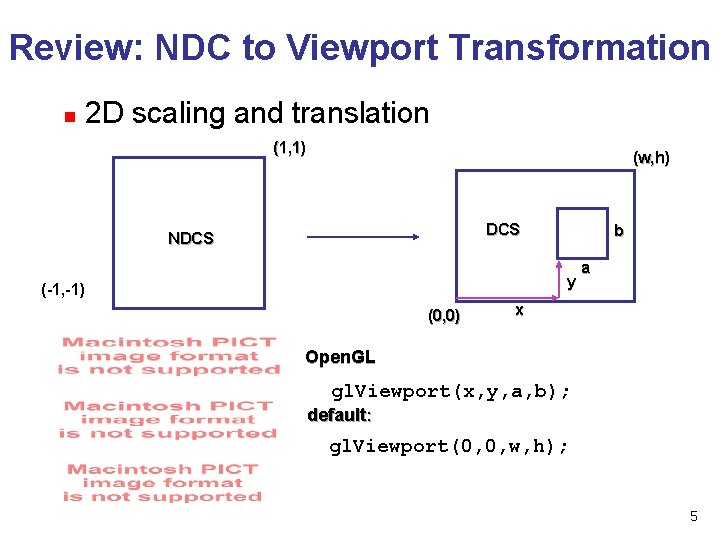
Review: NDC to Viewport Transformation n 2 D scaling and translation (1, 1) (w, h) DCS NDCS b y (-1, -1) (0, 0) a x Open. GL gl. Viewport(x, y, a, b); default: gl. Viewport(0, 0, w, h); 5

Review: Perspective Normalization n n perspective viewing frustum transformed to cube orthographic rendering of cube produces same image as perspective rendering of original frustum 6

Review: Perspective Normalization viewing VCS projection transformation alter w n normalized device NDCS perspective clipping CCS perspective division /w distort such that orthographic projection of distorted objects is desired persp projection n separate division from standard matrix multiplies clip after warp, before divide division: normalization 7

Review: Coordinate Systems http: //www. btinternet. com/~danbgs/perspective/ 8

Review: Perspective Derivation VCS z NDCS y=top x=left (1, 1, 1) y y z (-1, -1) x y=bottom z=-near x=right z=-far x 9

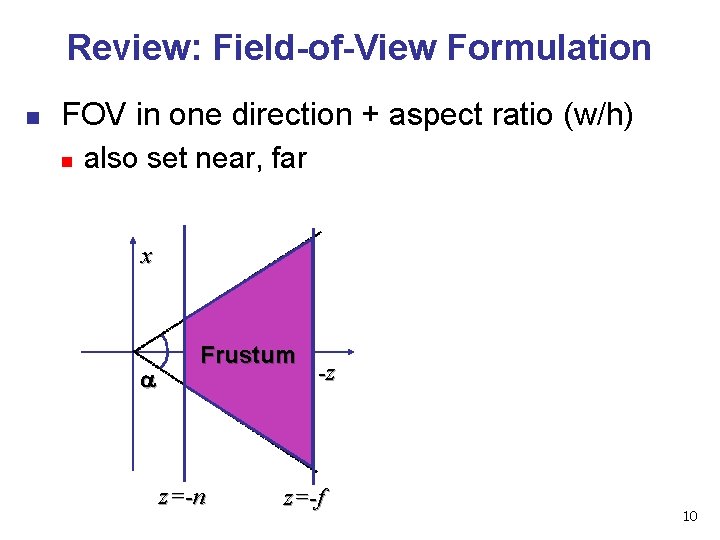
Review: Field-of-View Formulation n FOV in one direction + aspect ratio (w/h) n also set near, far x Frustum z=-n -z z=-f 10

Projection Taxonomy planar projections perspective: 1, 2, 3 -point parallel oblique cabinet orthographic cavalier top, front, side axonometric: isometric dimetric trimetric http: //ceprofs. tamu. edu/tkramer/ENGR%20111/5. 1/20 11

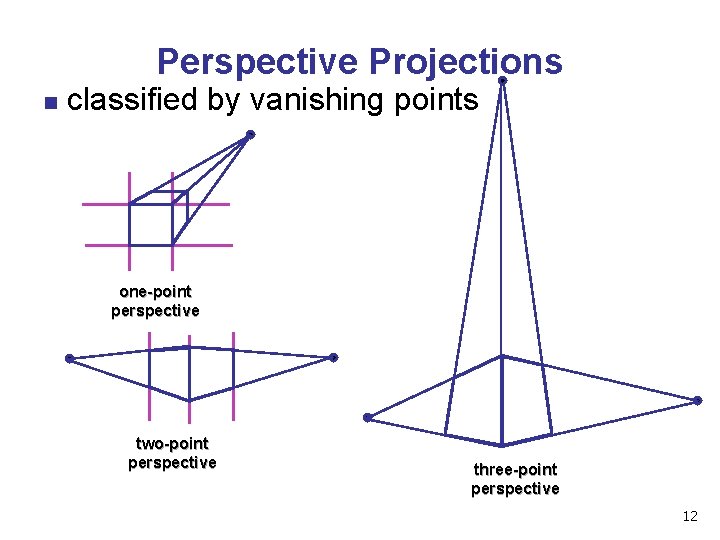
Perspective Projections n classified by vanishing points one-point perspective two-point perspective three-point perspective 12

Parallel Projection n projectors are all parallel n n n vs. perspective projectors that converge orthographic: projectors perpendicular to projection plane oblique: projectors not necessarily perpendicular to projection plane Orthographic Oblique

Axonometric Projections n n projectors perpendicular to image plane select axis lengths http: //ceprofs. tamu. edu/tkramer/ENGR%20111/5. 1/20 14

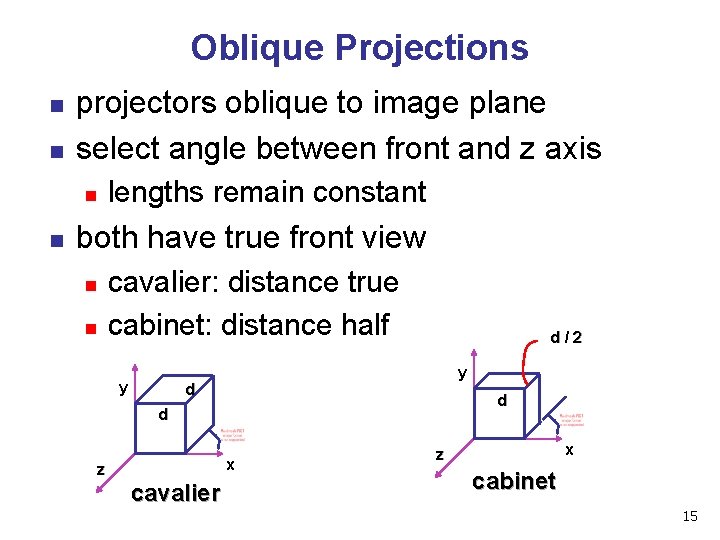
Oblique Projections n n projectors oblique to image plane select angle between front and z axis n n lengths remain constant both have true front view n n cavalier: distance true cabinet: distance half y d/2 y d d d x z cavalier x z cabinet 15

Demos n Tuebingen applets from Frank Hanisch n http: //www. gris. uni-tuebingen. de/projects/grdev/doc/html/etc/ Applet. Index. html#Transformationen 16

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2005 Tamara Munzner Lighting: Illumination

Goal model interaction of light with matter in a way that appears realistic and is fast n phenomenological reflection models n n n ignore real physics, approximate the look simple, non-physical Phong, Blinn-Phong physically based reflection models simulate physics BRDFs: Bidirectional Reflection Distribution Functions 18

Photorealistic Illumination [electricimage. com] 19

Photorealistic Illumination [electricimage. com] 20

Fast Local Illumination 21

Illumination transport of energy from light sources to surfaces & points n n includes direct and indirect illumination Images by Henrik Wann Jensen 22

Components of Illumination two components: light sources and surface properties n light sources (or emitters) n spectrum of emittance (i. e. , color of the light) n geometric attributes n n n position direction shape directional attenuation polarization 23

Components of Illumination surface properties n reflectance spectrum (i. e. , color of the surface) n subsurface reflectance n geometric attributes n n position orientation micro-structure 24

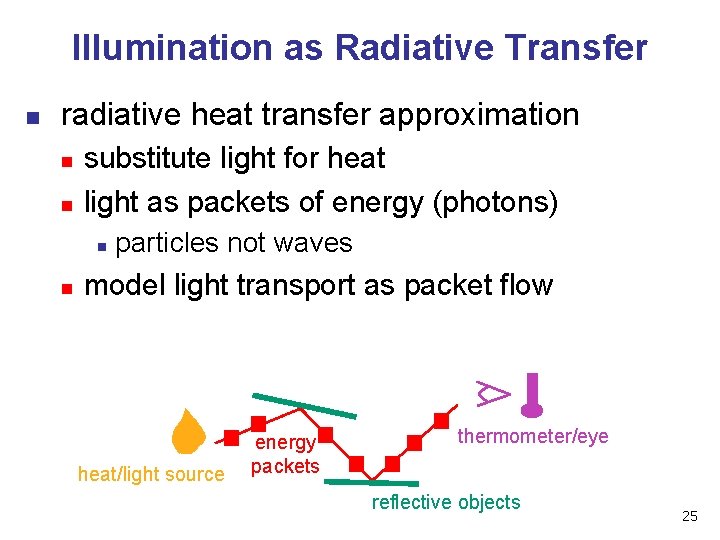
Illumination as Radiative Transfer n radiative heat transfer approximation n n substitute light for heat light as packets of energy (photons) n n particles not waves model light transport as packet flow heat/light source energy packets thermometer/eye reflective objects 25

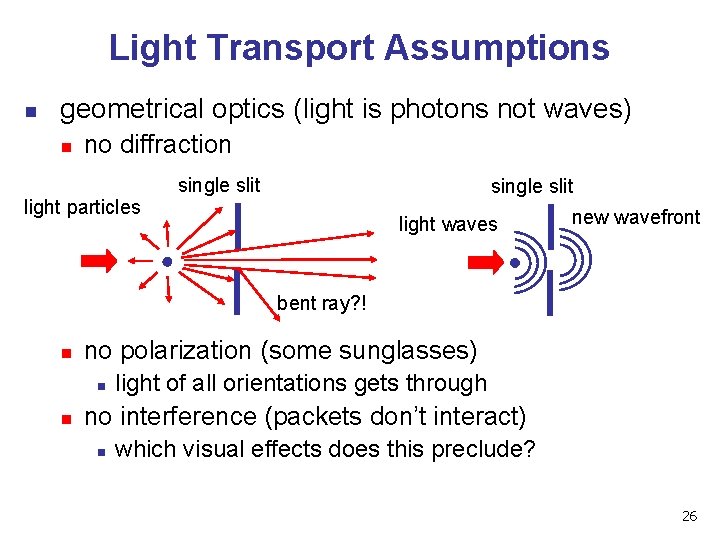
Light Transport Assumptions n geometrical optics (light is photons not waves) n no diffraction single slit light particles light waves new wavefront bent ray? ! n no polarization (some sunglasses) n n light of all orientations gets through no interference (packets don’t interact) n which visual effects does this preclude? 26

Light Transport Assumptions II n color approximated by discrete wavelengths n n n quantized approx of dispersion (rainbows) quantized approx of fluorescence (cycling vests) no propagation media (surfaces in vacuum) n no atmospheric scattering (fog, clouds) n n n some tricks to simulate explicitly no refraction (mirages) light travels in straight line n no gravity lenses 27

Light Transport Assumptions III n light travels in straight line n n no gravity lenses superposition (lights can be added) n no nonlinear reflection models n nonlinearity handled separately 28

Light Sources and Materials n n n n n appearance depends on light sources, locations, properties material (surface) properties viewer position local illumination compute at material, from light to viewer global illumination (later in course) ray tracing: from viewer into scene radiosity: between surface patches 29

Illumination in the Pipeline n n n local illumination only models light arriving directly from light source no interreflections and shadows n n n can be added through tricks, multiple rendering passes light sources simple shapes materials simple, non-physical reflection models 30

Light Sources n types of light sources n gl. Lightfv(GL_LIGHT 0, GL_POSITION, light[]) n directional/parallel lights n n n point lights n n real-life example: sun infinitely far source: homogeneous coord w=0 same intensity in all directions spot lights n limited set of directions: n point+direction+cutoff angle 31

Light Sources n n area lights light sources with a finite area more realistic model of many light sources not available with projective rendering pipeline, (i. e. , not available with Open. GL) 32

Light Sources n n n ambient lights no identifiable source or direction hack for replacing true global illumination n (light bouncing off from other objects) 33

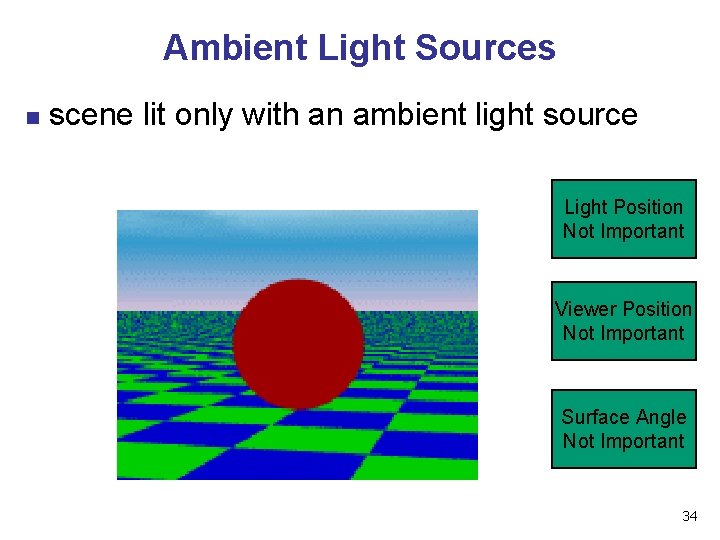
Ambient Light Sources n scene lit only with an ambient light source Light Position Not Important Viewer Position Not Important Surface Angle Not Important 34

Directional Light Sources n scene lit with directional and ambient light Light Position Not Important Surface Angle Important Viewer Position Not Important 35

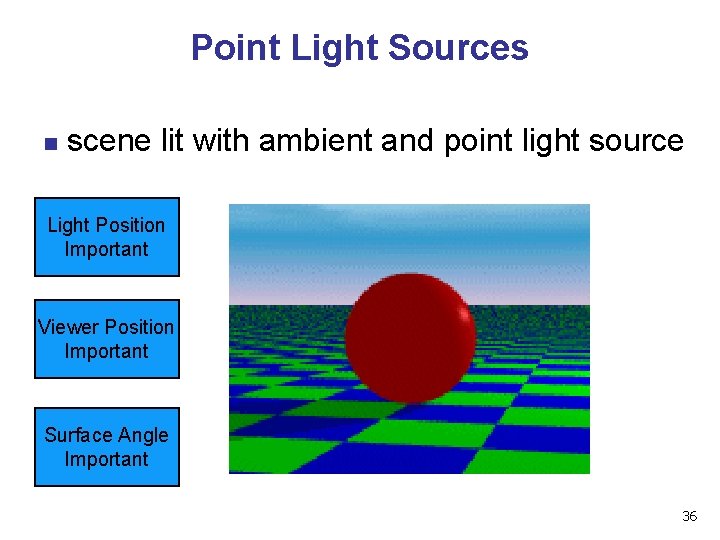
Point Light Sources n scene lit with ambient and point light source Light Position Important Viewer Position Important Surface Angle Important 36

Light Sources n n geometry: positions and directions standard: world coordinate system n n n alternative: camera coordinate system n n n effect: lights fixed wrt world geometry demo: http: //www. xmission. com/~nate/tutors. html effect: lights attached to camera (car headlights) points and directions undergo normal model/view transformation illumination calculations: camera coords 37

Types of Reflection n specular (a. k. a. mirror or regular) reflection causes light to propagate without scattering. diffuse reflection sends light in all directions with equal energy. mixed reflection is a weighted combination of specular and diffuse. 38

Types of Reflection n n retro-reflection occurs when incident energy reflects in directions close to the incident direction, for a wide range of incident directions. gloss is the property of a material surface that involves mixed reflection and is responsible for the mirror like appearance of rough surfaces. 39

Reflectance Distribution Model n most surfaces exhibit complex reflectances n n vary with incident and reflected directions. model with combination + + = specular + glossy + diffuse = reflectance distribution 40

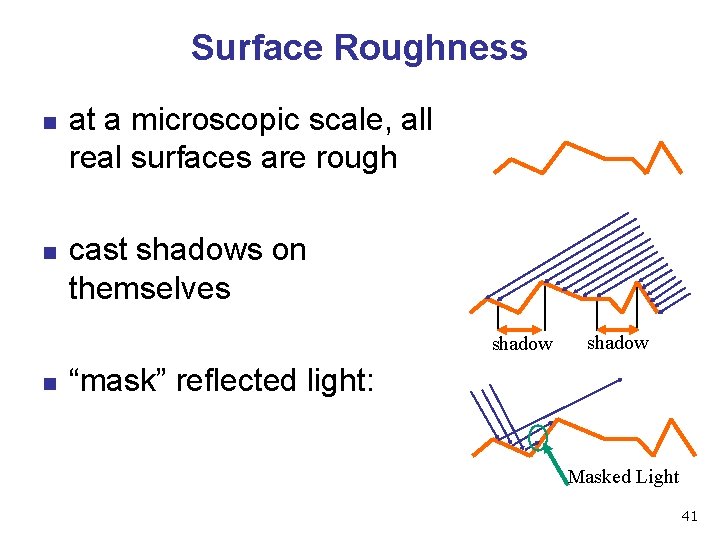
Surface Roughness n n at a microscopic scale, all real surfaces are rough cast shadows on themselves shadow n shadow “mask” reflected light: Masked Light 41

Surface Roughness n notice another effect of roughness: n n n each “microfacet” is treated as a perfect mirror. incident light reflected in different directions by different facets. end result is mixed reflectance. n n smoother surfaces are more specular or glossy. random distribution of facet normals results in diffuse reflectance. 42

Physics of Reflection n n ideal diffuse reflection very rough surface at the microscopic level n n n real-world example: chalk microscopic variations mean incoming ray of light equally likely to be reflected in any direction over the hemisphere what does the reflected intensity depend on? 43

Lambert’s Cosine Law n ideal diffuse surface reflection the energy reflected by a small portion of a surface from a light source in a given direction is proportional to the cosine of the angle between that direction and the surface normal n n reflected intensity independent of viewing direction depends on surface orientation wrt light often called Lambertian surfaces 44

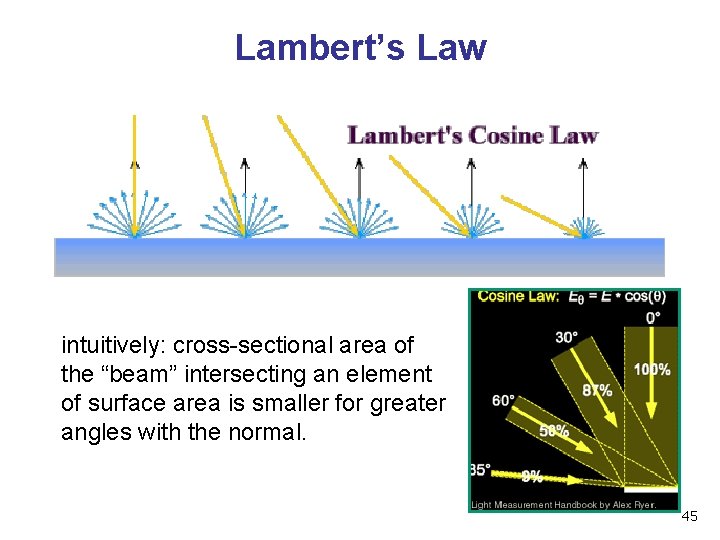
Lambert’s Law intuitively: cross-sectional area of the “beam” intersecting an element of surface area is smaller for greater angles with the normal. 45

Computing Diffuse Reflection angle between surface normal and incoming light is angle of incidence: kd : l n diffuse component n Idiffuse = kd Ilight cos n ”surface color” in practice use vector arithmetic Idiffuse = kd Ilight (n • l) 46

Diffuse Lighting Examples Lambertian sphere from several lighting angles: n n need only consider angles from 0° to 90° why? demo: Brown exploratory on reflection 47