University of British Columbia CPSC 314 Computer Graphics

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2016 Tamara Munzner Transformations http: //www. ugrad. cs. ubc. ca/~cs 314/Vjan 2016

Readings for Transformations 1 -5 • Shirley/Marschner • Ch 6: Transformation Matrices • except 6. 1. 6, 6. 3. 1 • Sect 12. 2 Scene Graphs • Gortler • • Ch 2: Linear, Sec 2. 5 -2. 6 Ch 3: Affine Ch 4: Respect Ch 5: Frames in Graphics, 5. 3 -5. 4 2

2 D Transformations 3

Transformations • transforming an object = transforming all its points • transforming a polygon = transforming its vertices 4

Matrix Representation • represent 2 D transformation with matrix • multiply matrix by column vector apply transformation to point • transformations combined by multiplication • matrices are efficient, convenient way to represent sequence of transformations! 5

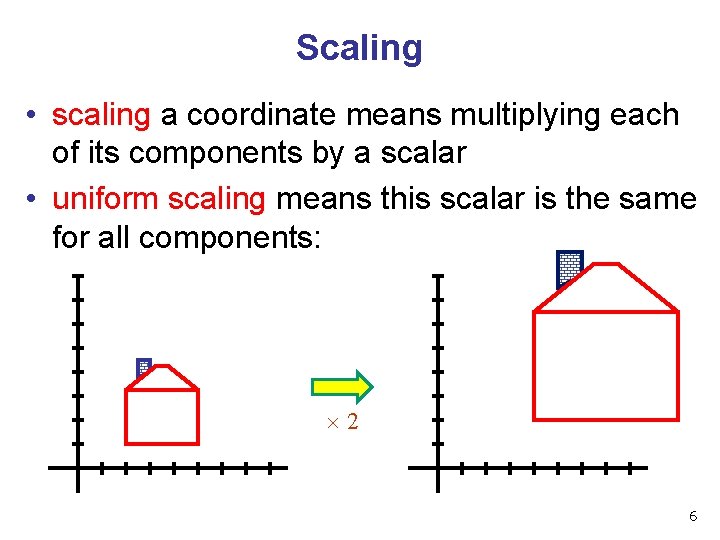
Scaling • scaling a coordinate means multiplying each of its components by a scalar • uniform scaling means this scalar is the same for all components: 2 6

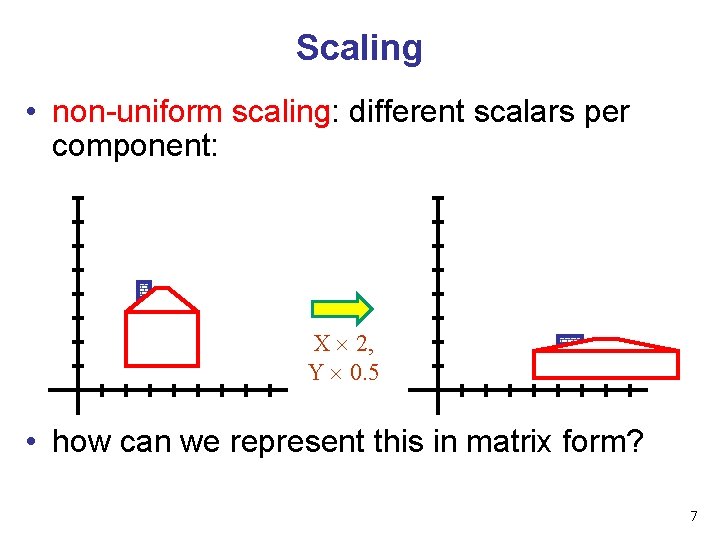
Scaling • non-uniform scaling: different scalars per component: X 2, Y 0. 5 • how can we represent this in matrix form? 7

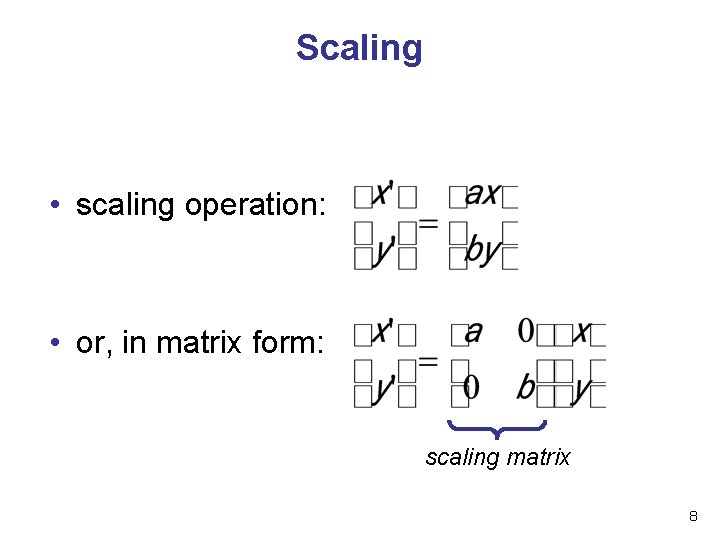
Scaling • scaling operation: • or, in matrix form: scaling matrix 8

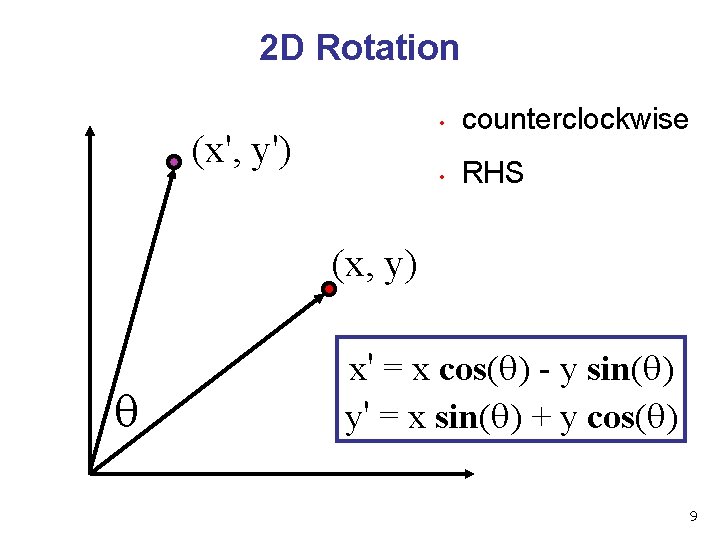
2 D Rotation (x', y') • counterclockwise • RHS (x, y) x' = x cos( ) - y sin( ) y' = x sin( ) + y cos( ) 9

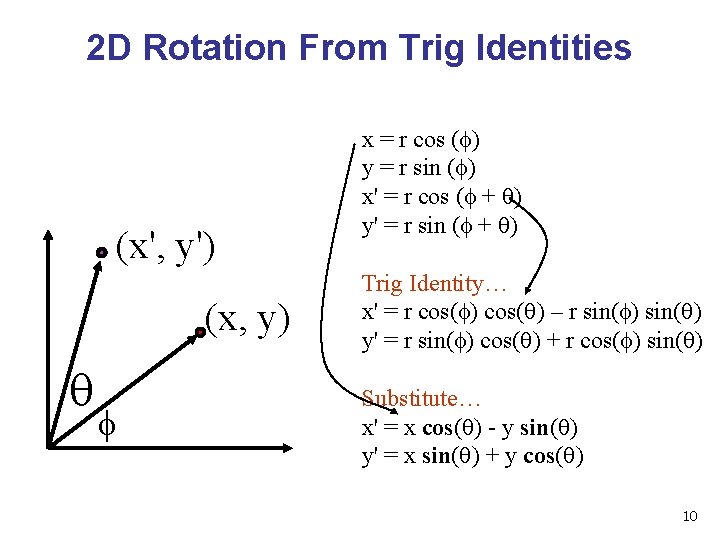
2 D Rotation From Trig Identities (x', y') (x, y) f x = r cos (f) y = r sin (f) x' = r cos (f + ) y' = r sin (f + ) Trig Identity… x' = r cos(f) cos( ) – r sin(f) sin( ) y' = r sin(f) cos( ) + r cos(f) sin( ) Substitute… x' = x cos( ) - y sin( ) y' = x sin( ) + y cos( ) 10

2 D Rotation: Another Derivation (x', y') q (x, y) 11

2 D Rotation: Another Derivation (x', y') q (x, y) x y 12

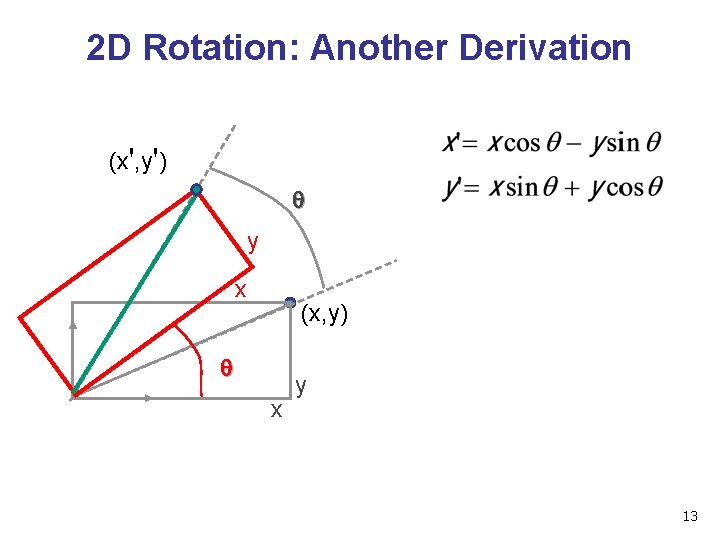
2 D Rotation: Another Derivation (x', y') q y x (x, y) q x y 13

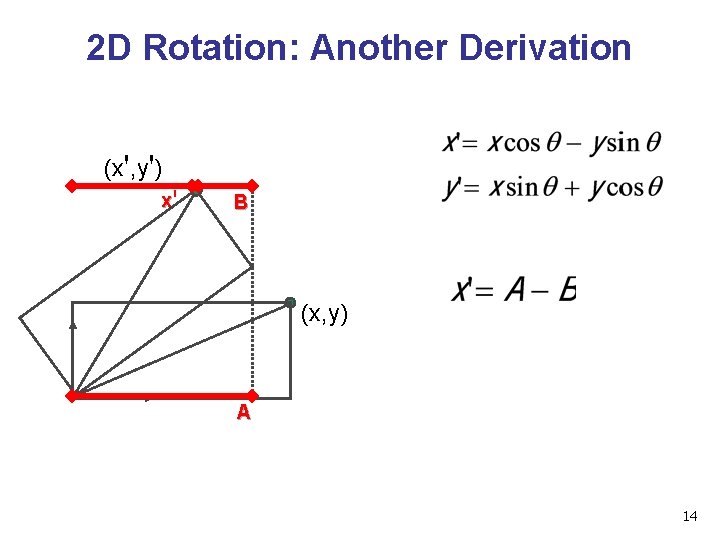
2 D Rotation: Another Derivation (x', y') x' B (x, y) A 14

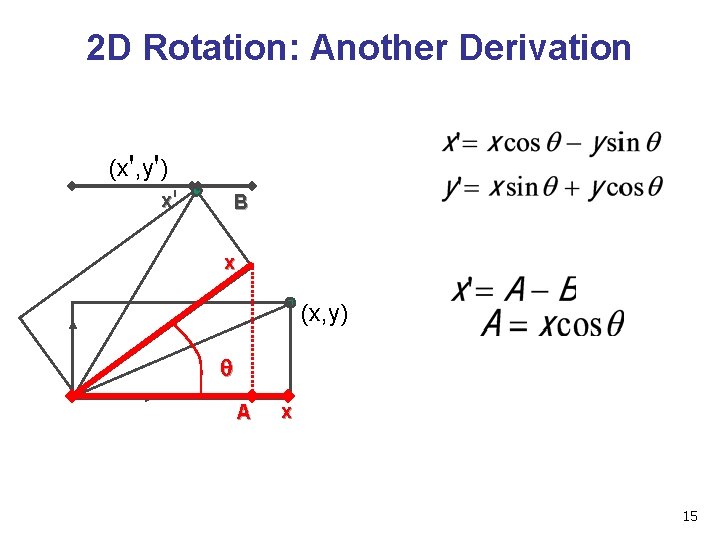
2 D Rotation: Another Derivation (x', y') x' B x (x, y) q A x 15

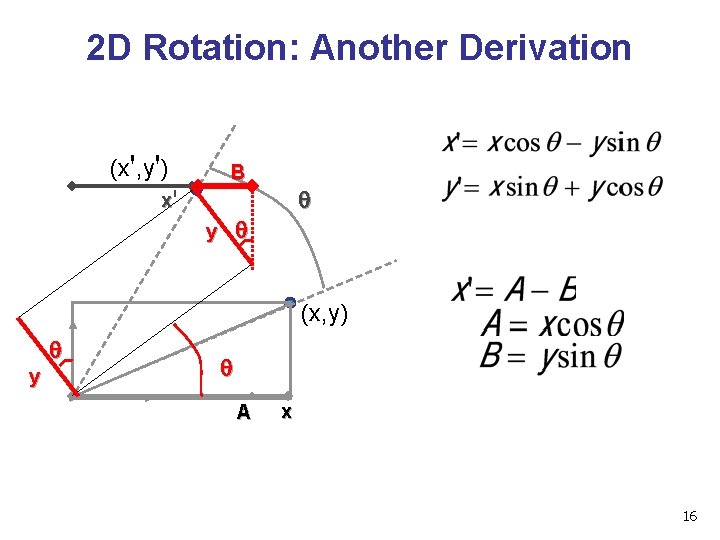
2 D Rotation: Another Derivation (x', y') B x' q q y (x, y) q y q A x 16

2 D Rotation Matrix • easy to capture in matrix form: • even though sin(q) and cos(q) are nonlinear functions of q, • x' is a linear combination of x and y • y' is a linear combination of x and y 17

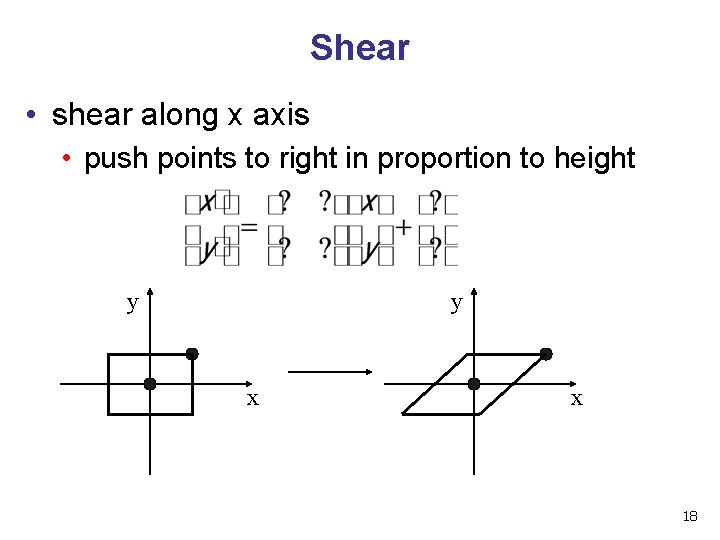
Shear • shear along x axis • push points to right in proportion to height y y x x 18

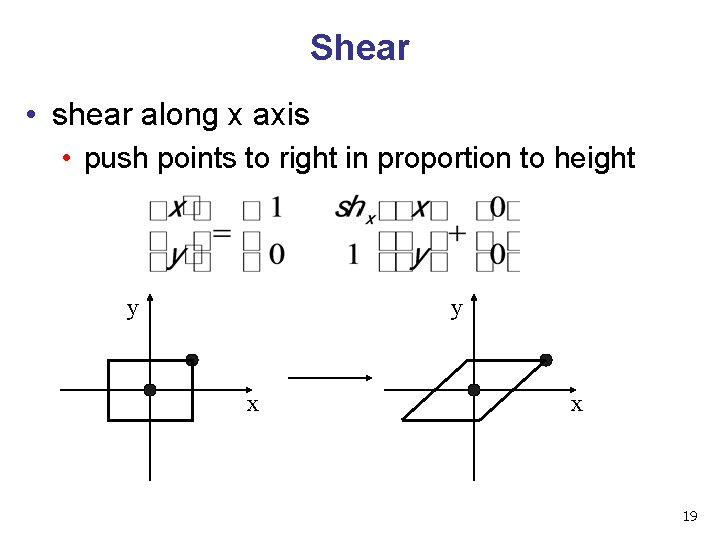
Shear • shear along x axis • push points to right in proportion to height y y x x 19

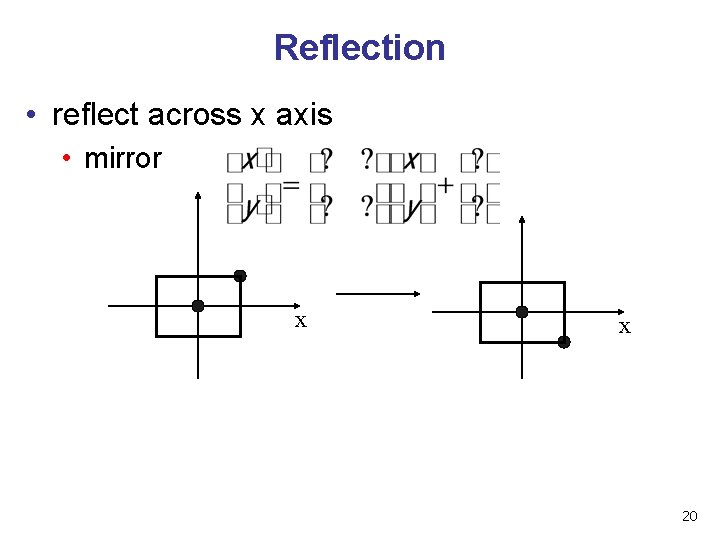
Reflection • reflect across x axis • mirror x x 20

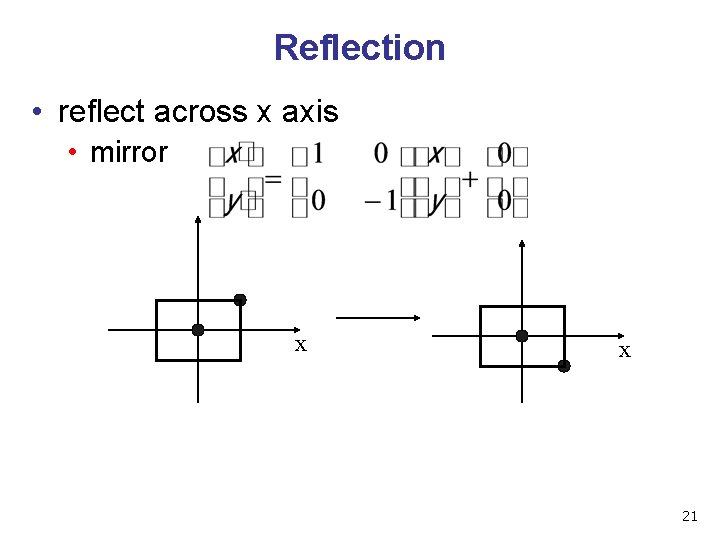
Reflection • reflect across x axis • mirror x x 21

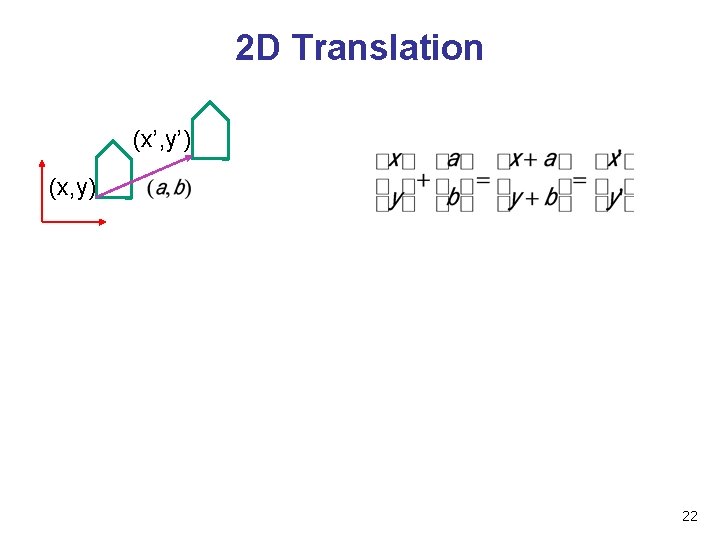
2 D Translation (x’, y’) (x, y) 22

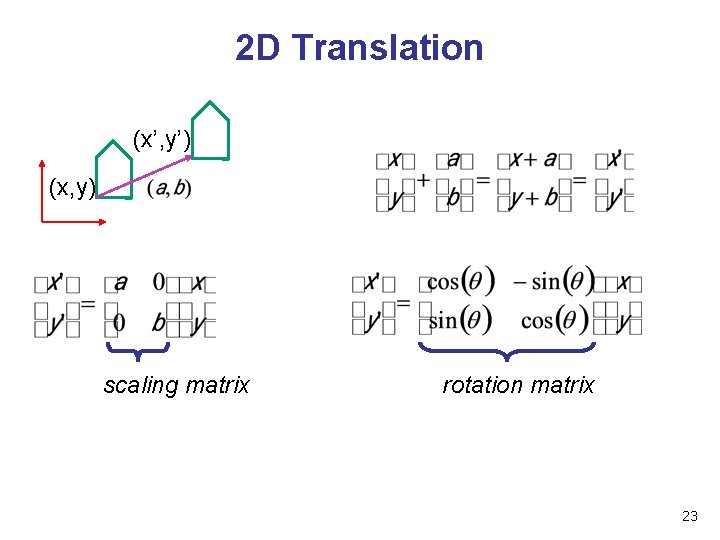
2 D Translation (x’, y’) (x, y) scaling matrix rotation matrix 23

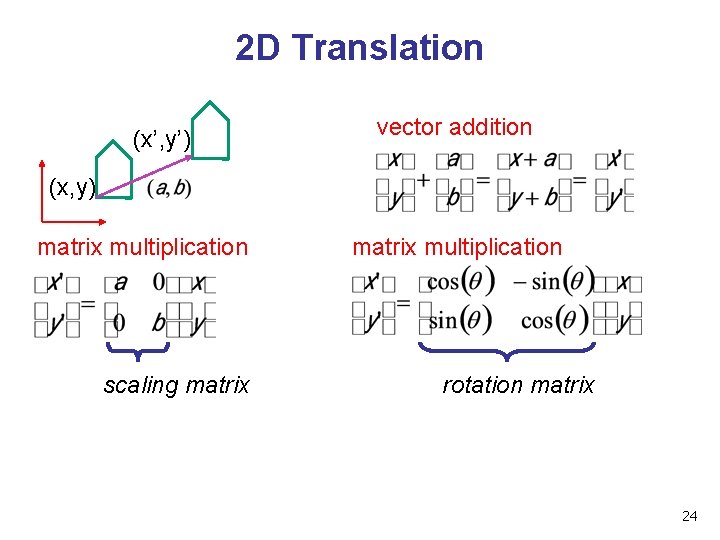
2 D Translation (x’, y’) vector addition (x, y) matrix multiplication scaling matrix multiplication rotation matrix 24

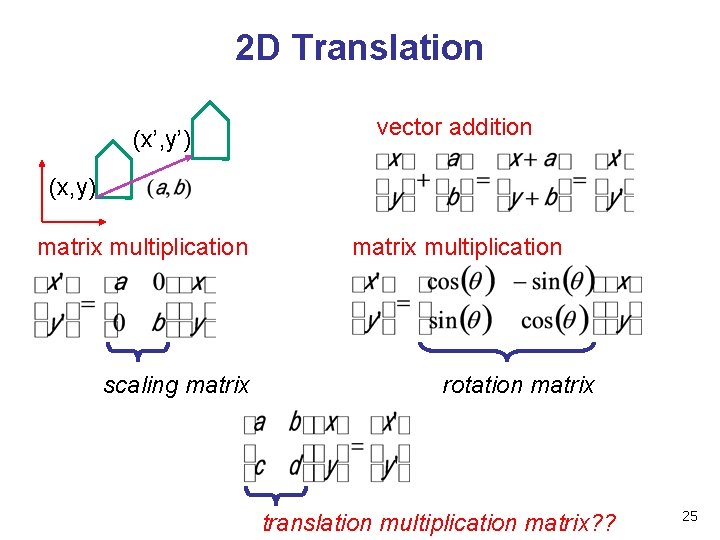
2 D Translation (x’, y’) vector addition (x, y) matrix multiplication scaling matrix multiplication rotation matrix translation multiplication matrix? ? 25

Linear Transformations • linear transformations are combinations of • • shear scale rotate reflect • properties of linear transformations • • • satisifes T(sx+ty) = s T(x) + t T(y) origin maps to origin lines map to lines parallel lines remain parallel ratios are preserved closed under composition 26

Challenge • matrix multiplication • for everything except translation • can we just do everything with multiplication? • then could just do composition, no special cases 27