University of British Columbia CPSC 314 Computer Graphics

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2005 Tamara Munzner Projections Week 4, Mon Jan 24 n http: //www. ugrad. cs. ubc. ca/~cs 314/Vjan 200 5

News n make sure you’ve signed up for demo slot 2

Review: Display Lists n reuse block of Open. GL code n n n efficiency multiple instances of same object static objects redrawn often exploit hierarchical structure when possible set up list once with gl. New. List/gl. End. List n call multiple times 3

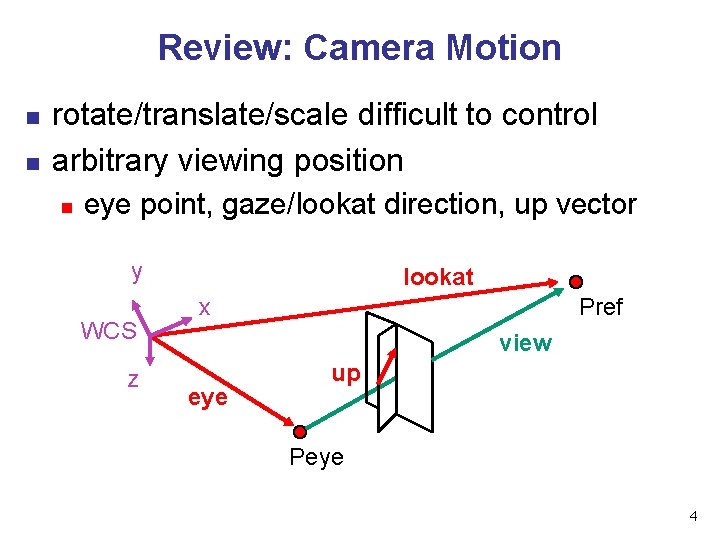
Review: Camera Motion n n rotate/translate/scale difficult to control arbitrary viewing position n eye point, gaze/lookat direction, up vector y WCS z lookat x Pref view eye up Peye 4

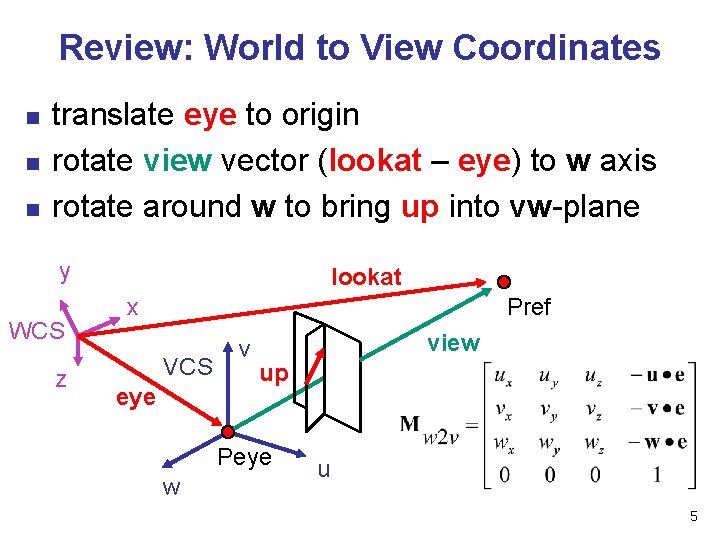
Review: World to View Coordinates n n n translate eye to origin rotate view vector (lookat – eye) to w axis rotate around w to bring up into vw-plane y WCS z lookat x Pref VCS eye v view up Peye w u 5

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2005 Tamara Munzner Projections

Pinhole Camera n n n www. kodak. com ingredients box film hole punch www. debevec. org/Pinhole results pictures! www. pinhole. org 7

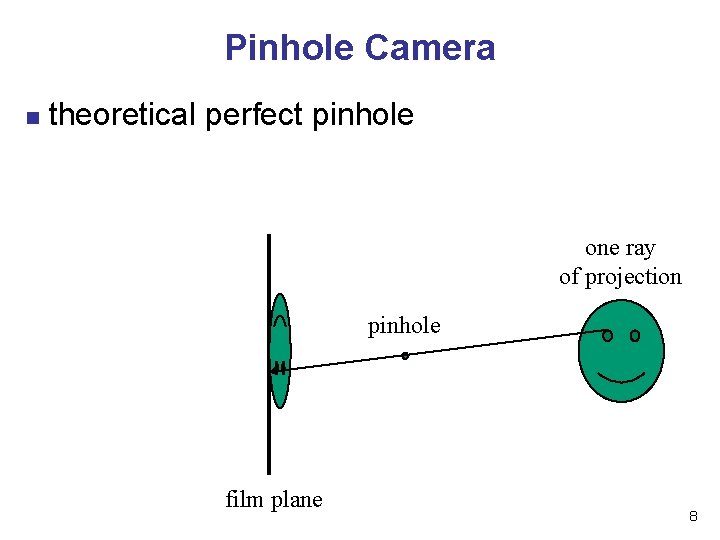
Pinhole Camera n theoretical perfect pinhole one ray of projection pinhole film plane 8

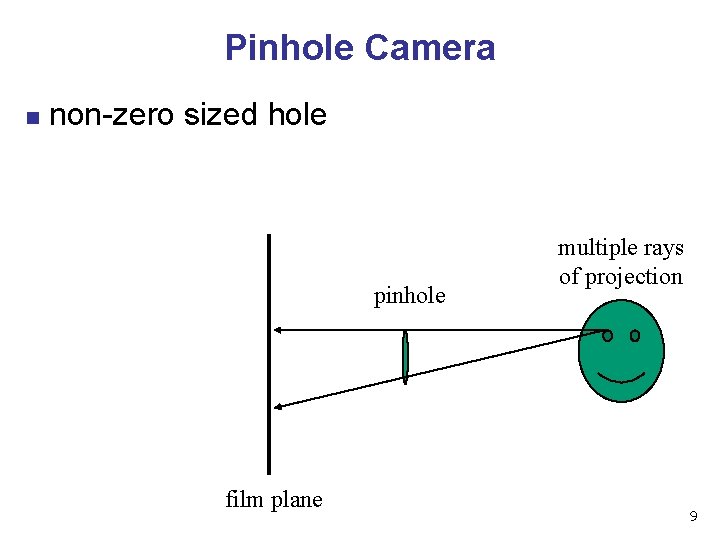
Pinhole Camera n non-zero sized hole pinhole film plane multiple rays of projection 9

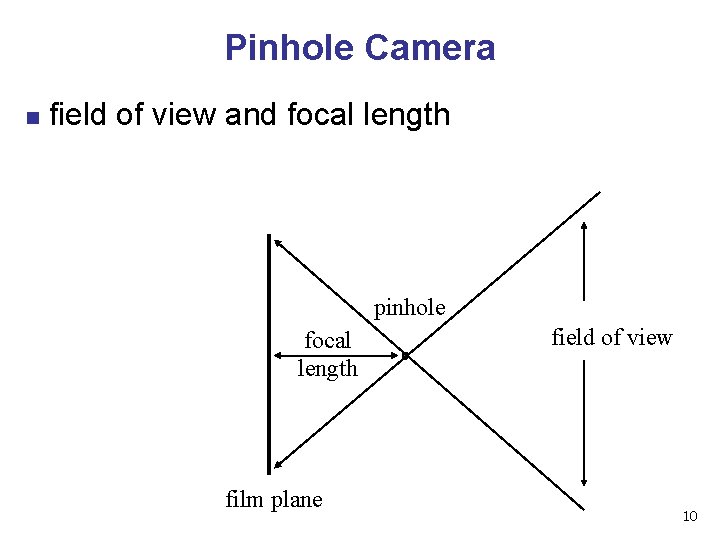
Pinhole Camera n field of view and focal length pinhole focal length film plane field of view 10

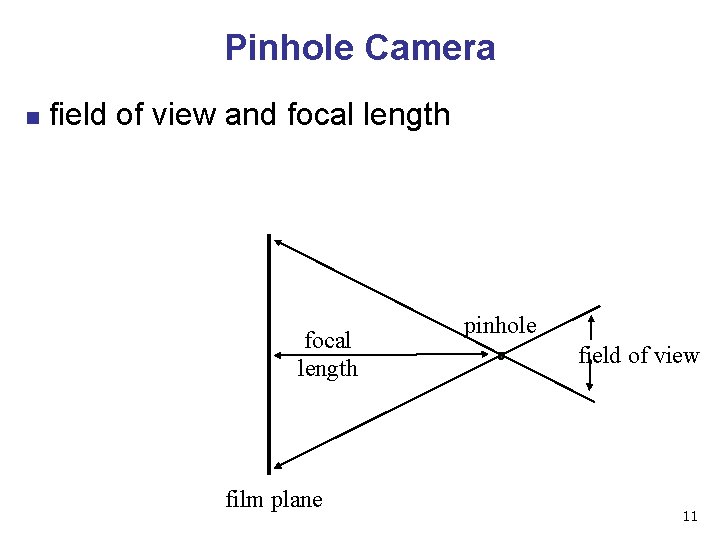
Pinhole Camera n field of view and focal length film plane pinhole field of view 11

Real Cameras n pinhole camera has small aperture (lens opening) n hard to get enough light to expose the film real pinhole camera aperture n n lens permits larger apertures lens permits changing distance to film plane without actually moving the film plane camera f lens price to pay: limited depth of field 12

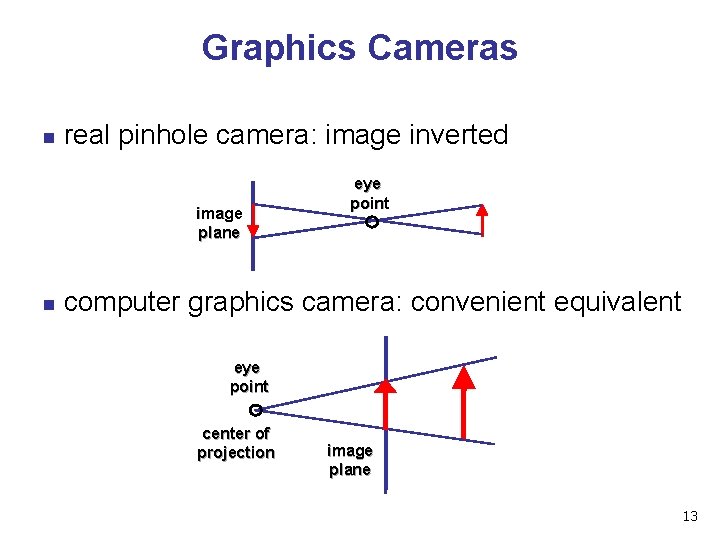
Graphics Cameras n real pinhole camera: image inverted image plane n eye point computer graphics camera: convenient equivalent eye point center of projection image plane 13

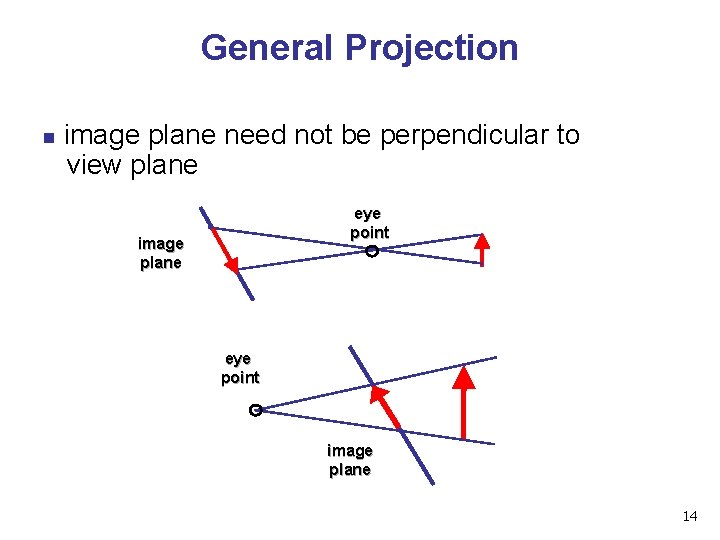
General Projection n image plane need not be perpendicular to view plane eye point image plane 14

Perspective Projection n our camera must model perspective 15

Perspective Projection n our camera must model perspective 16

Perspective Projection n our camera must model perspective 17

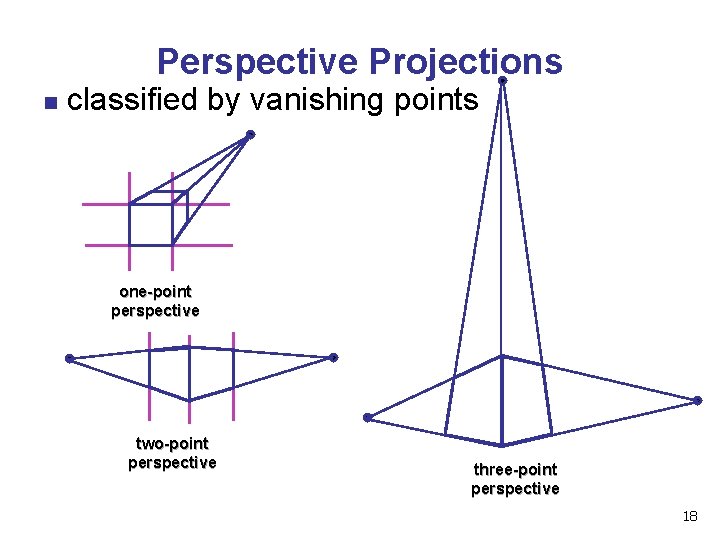
Perspective Projections n classified by vanishing points one-point perspective two-point perspective three-point perspective 18

Projective Transformations n n planar geometric projections planar: onto a plane geometric: using straight lines projections: 3 D -> 2 D n aka projective mappings n counterexamples? 19

Projective Transformations n n n properties lines mapped to lines and triangles to triangles parallel lines do NOT remain parallel n n e. g. rails vanishing at infinity affine combinations are NOT preserved n e. g. center of a line does not map to center of projected line (perspective foreshortening) 20

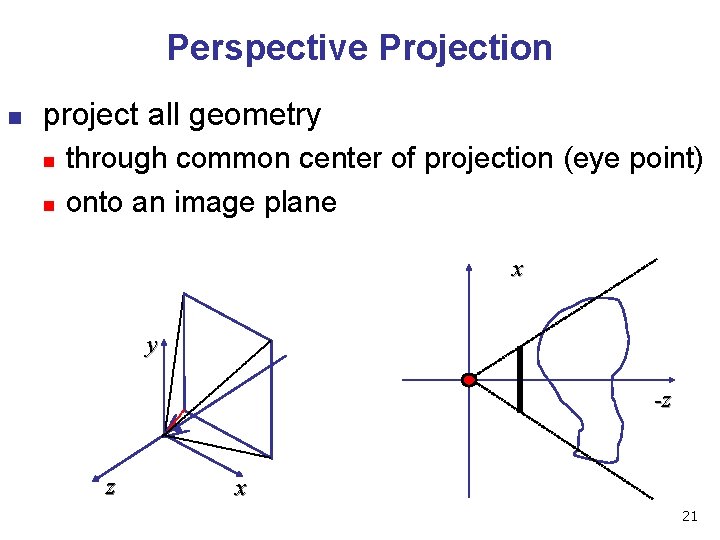
Perspective Projection n project all geometry n n through common center of projection (eye point) onto an image plane x y -z z x 21

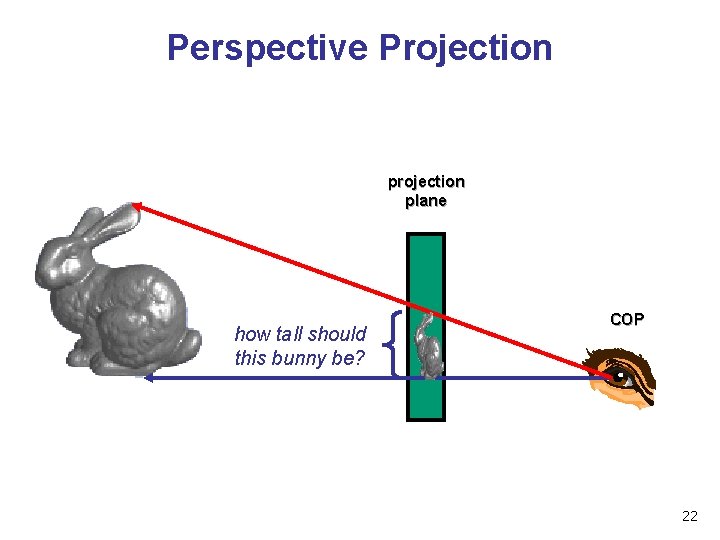
Perspective Projection plane how tall should this bunny be? COP 22

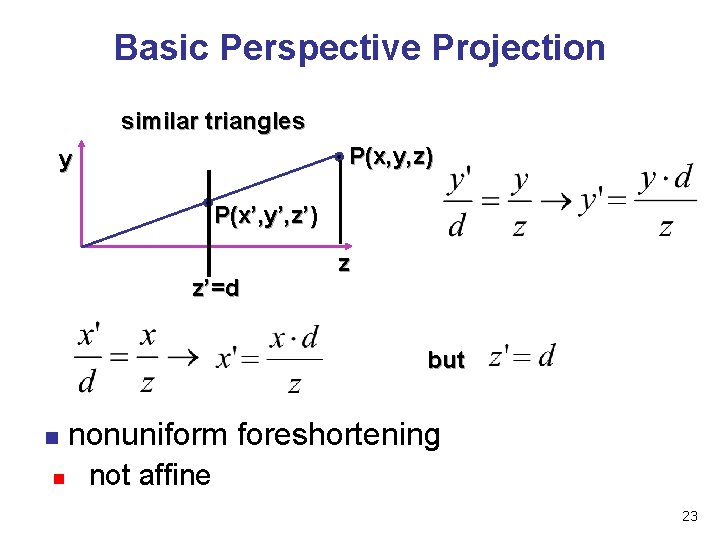
Basic Perspective Projection similar triangles P(x, y, z) y P(x’, y’, z’) z’=d z but n n nonuniform foreshortening not affine 23

Perspective Projection n n desired result for a point [x, y, z, 1]T projected onto the view plane: what could a matrix look like to do this? 24

Perspective Projection Matrix 25

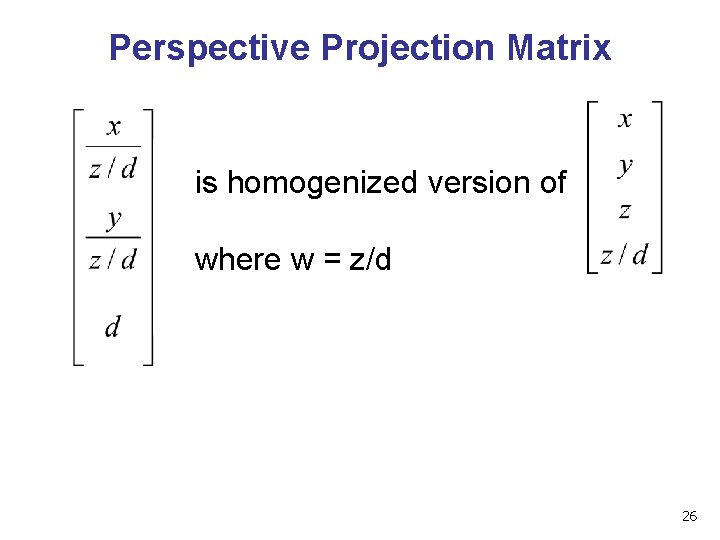
Perspective Projection Matrix is homogenized version of where w = z/d 26

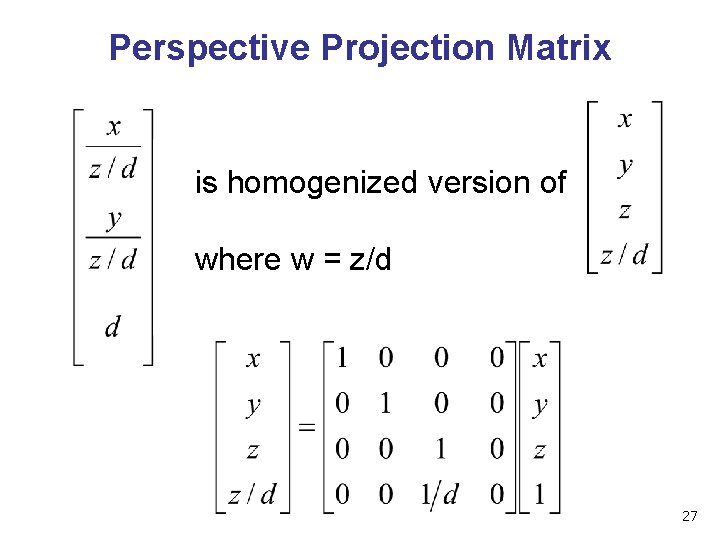
Perspective Projection Matrix is homogenized version of where w = z/d 27

Perspective Projection n expressible with 4 x 4 homogeneous matrix n n use previously untouched bottom row perspective projection is irreversible n n many 3 D points can be mapped to same (x, y, d) on the projection plane no way to retrieve the unique z values 28

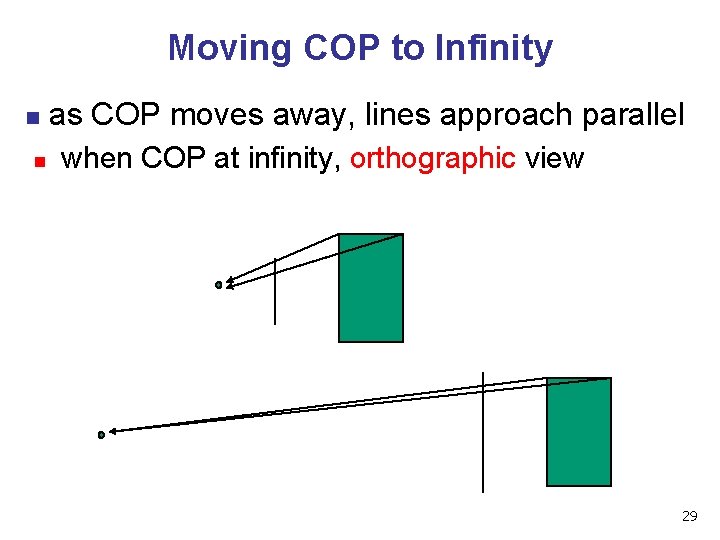
Moving COP to Infinity n n as COP moves away, lines approach parallel when COP at infinity, orthographic view 29

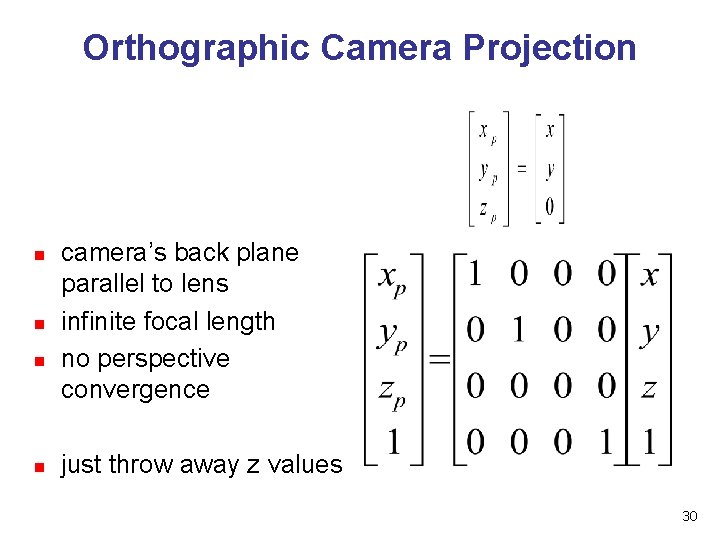
Orthographic Camera Projection n n camera’s back plane parallel to lens infinite focal length no perspective convergence just throw away z values 30

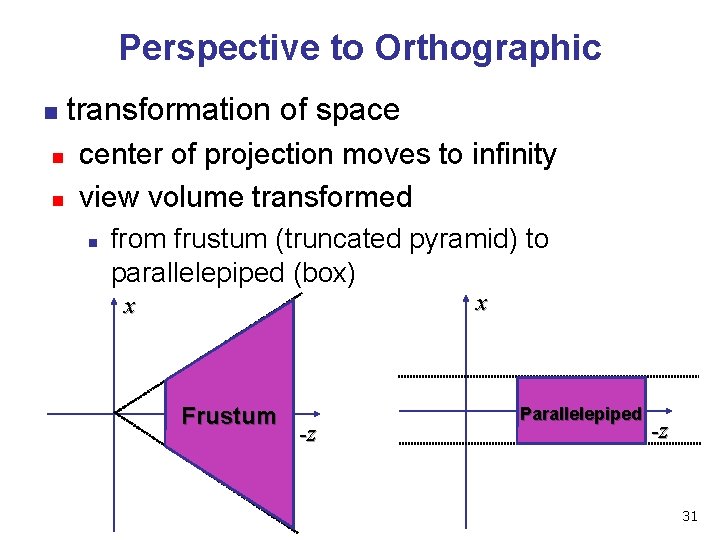
Perspective to Orthographic n n n transformation of space center of projection moves to infinity view volume transformed n from frustum (truncated pyramid) to parallelepiped (box) x x Frustum -z Parallelepiped -z 31

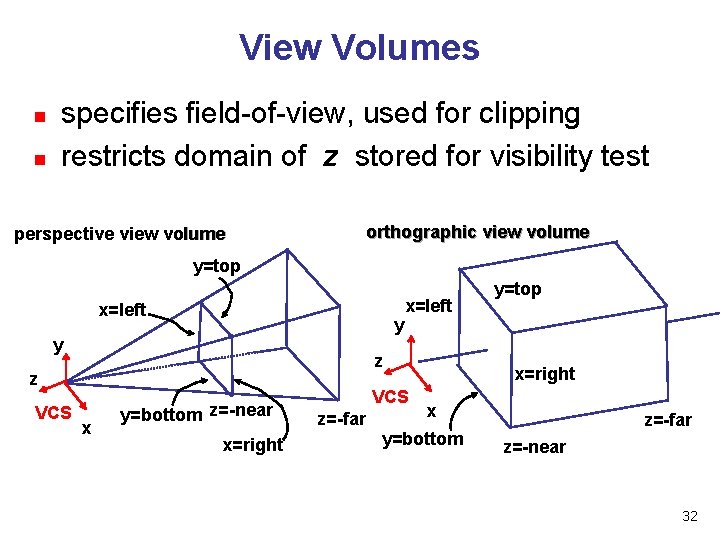
View Volumes n n specifies field-of-view, used for clipping restricts domain of z stored for visibility test orthographic view volume perspective view volume y=top x=left y y z z VCS x=left x y=bottom z=-near x=right VCS z=-far y=top x=right x y=bottom z=-far z=-near 32

View Volume n convention n viewing frustum mapped to specific parallelepiped Normalized Device Coordinates (NDC) n same as clipping coords n n n only objects inside the parallelepiped get rendered which parallelepiped? n depends on rendering system 33

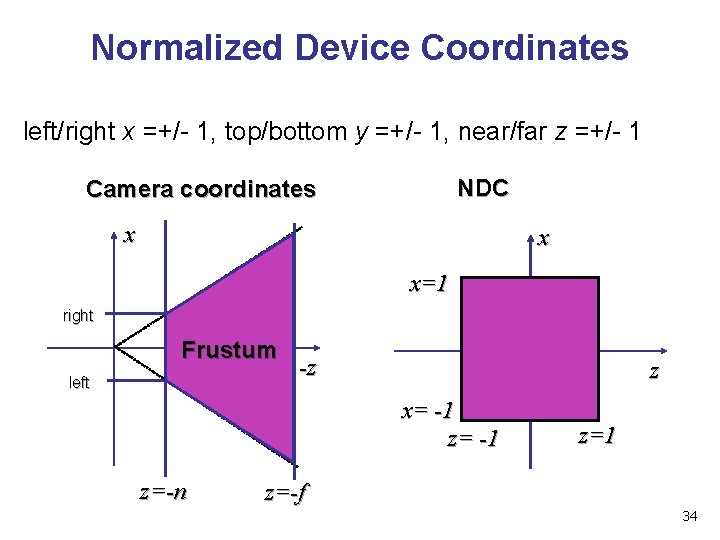
Normalized Device Coordinates left/right x =+/- 1, top/bottom y =+/- 1, near/far z =+/- 1 NDC Camera coordinates x x x=1 right Frustum left -z z x= -1 z=-n z=1 z=-f 34

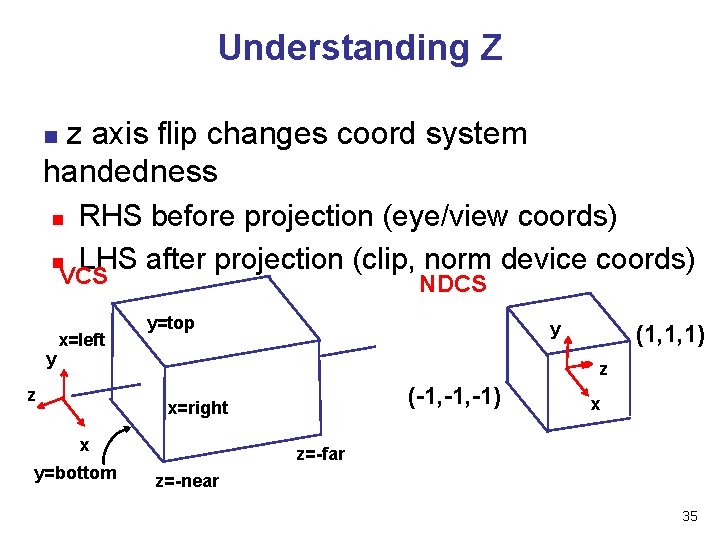
Understanding Z z axis flip changes coord system handedness n RHS before projection (eye/view coords) n LHS after projection (clip, norm device coords) VCS n NDCS y x=left y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 35

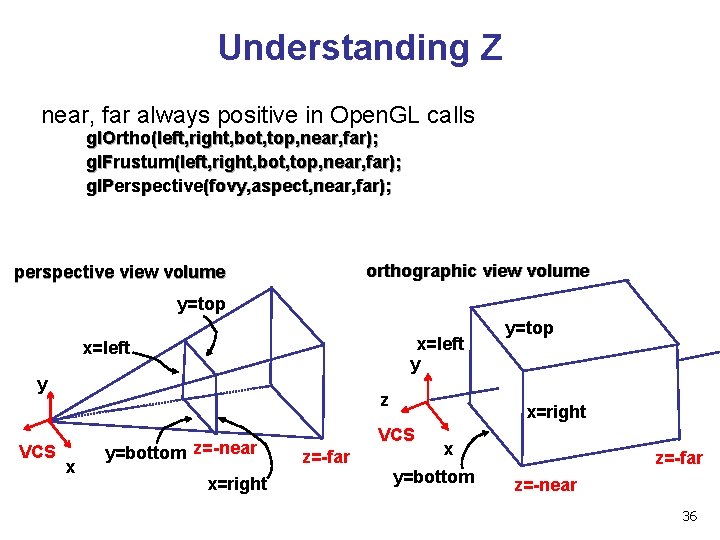
Understanding Z near, far always positive in Open. GL calls gl. Ortho(left, right, bot, top, near, far); gl. Frustum(left, right, bot, top, near, far); gl. Perspective(fovy, aspect, near, far); orthographic view volume perspective view volume y=top x=left y VCS z x y=bottom z=-near x=right VCS z=-far y=top x y=bottom z=-far z=-near 36

Understanding Z n why near and far plane? n near plane: n n avoid singularity (division by zero, or very small numbers) far plane: store depth in fixed-point representation (integer), thus have to have fixed range of values (0… 1) n avoid/reduce numerical precision artifacts for distant objects n 37

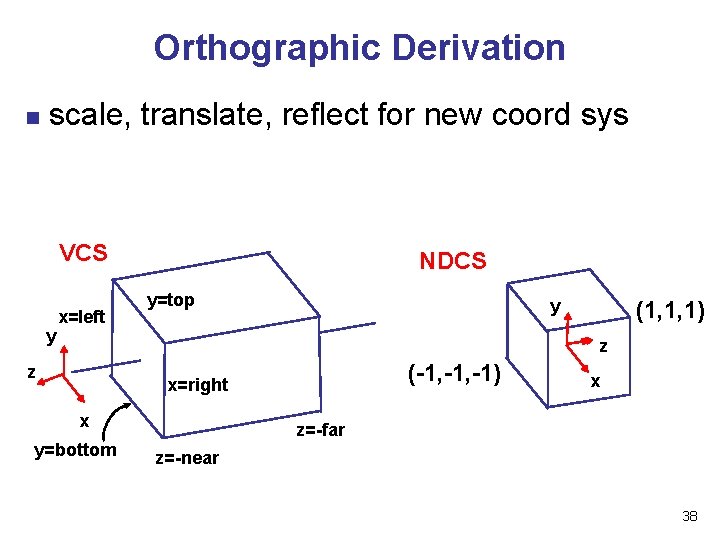
Orthographic Derivation n scale, translate, reflect for new coord sys VCS y x=left NDCS y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 38

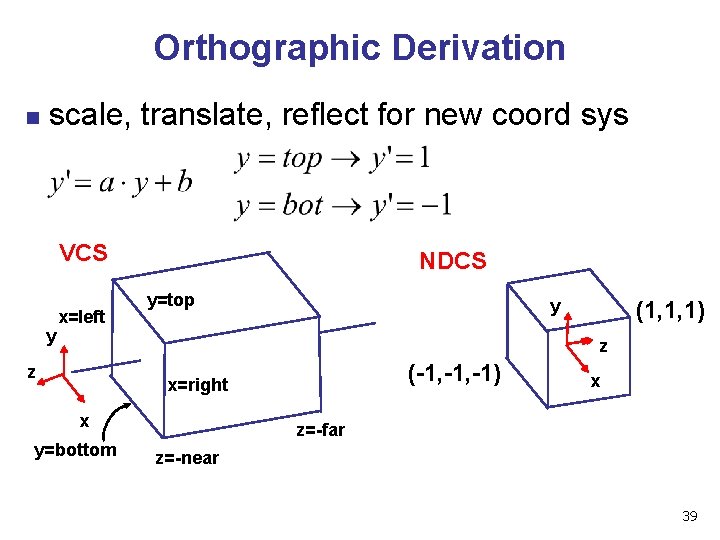
Orthographic Derivation n scale, translate, reflect for new coord sys VCS y x=left NDCS y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 39

Orthographic Derivation n scale, translate, reflect for new coord sys 40

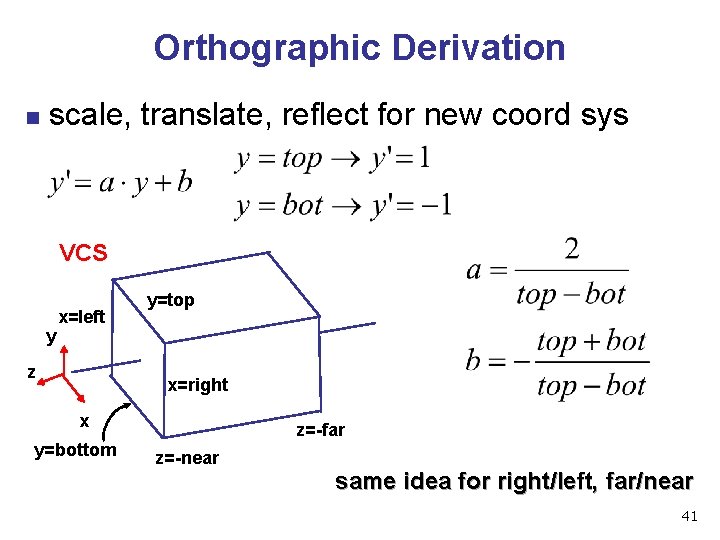
Orthographic Derivation n scale, translate, reflect for new coord sys VCS y x=left z y=top x=right x y=bottom z=-far z=-near same idea for right/left, far/near 41

Orthographic Derivation n scale, translate, reflect for new coord sys 42

Orthographic Derivation n scale, translate, reflect for new coord sys 43

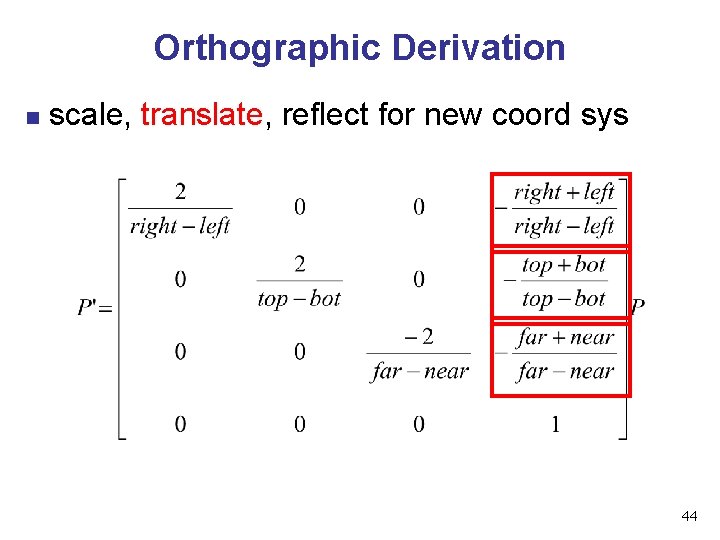
Orthographic Derivation n scale, translate, reflect for new coord sys 44

Orthographic Derivation n scale, translate, reflect for new coord sys 45

Orthographic Open. GL gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); gl. Ortho(left, right, bot, top, near, far); 46