University of British Columbia CPSC 314 Computer Graphics

University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2008 Tamara Munzner Viewing/Projections III Week 4, Wed Jan 30 • http: //www. ugrad. cs. ubc. ca/~cs 314/Vjan 2008

Review: Graphics Cameras • real pinhole camera: image inverted image plane n eye point computer graphics camera: convenient equivalent eye point center of projection image plane 2
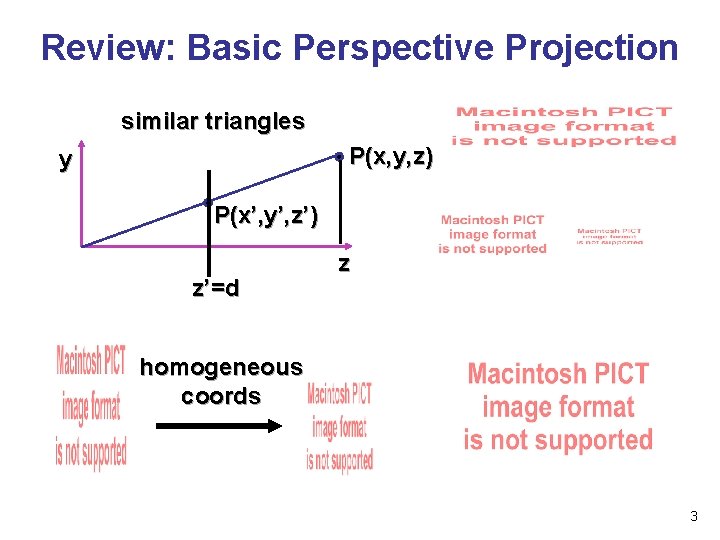
Review: Basic Perspective Projection similar triangles P(x, y, z) y P(x’, y’, z’) z’=d z homogeneous coords 3

Perspective Projection • expressible with 4 x 4 homogeneous matrix • use previously untouched bottom row • perspective projection is irreversible • many 3 D points can be mapped to same (x, y, d) on the projection plane • no way to retrieve the unique z values 4
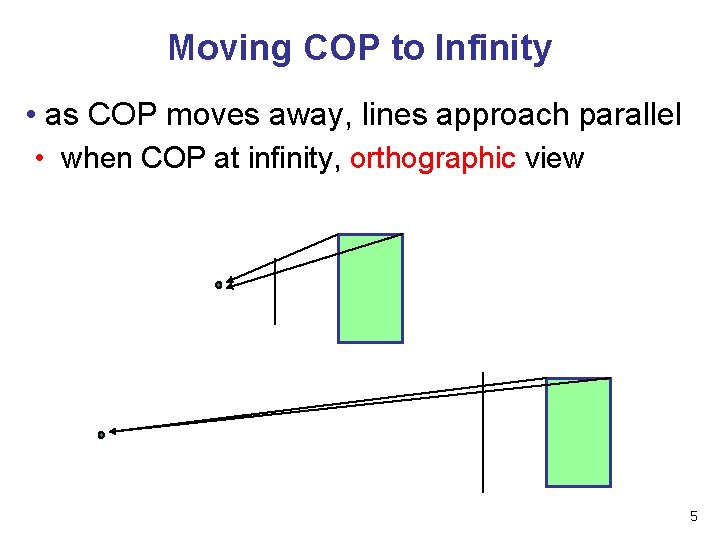
Moving COP to Infinity • as COP moves away, lines approach parallel • when COP at infinity, orthographic view 5

Orthographic Camera Projection • camera’s back plane parallel to lens • infinite focal length • no perspective convergence • just throw away z values 6
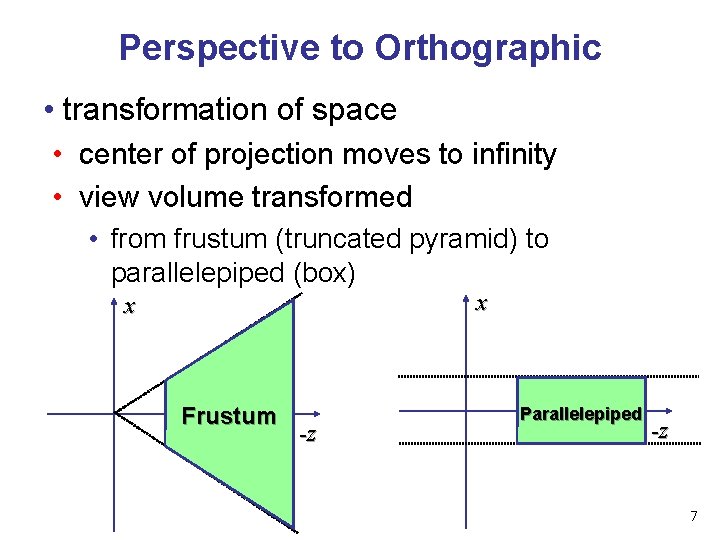
Perspective to Orthographic • transformation of space • center of projection moves to infinity • view volume transformed • from frustum (truncated pyramid) to parallelepiped (box) x x Frustum -z Parallelepiped -z 7
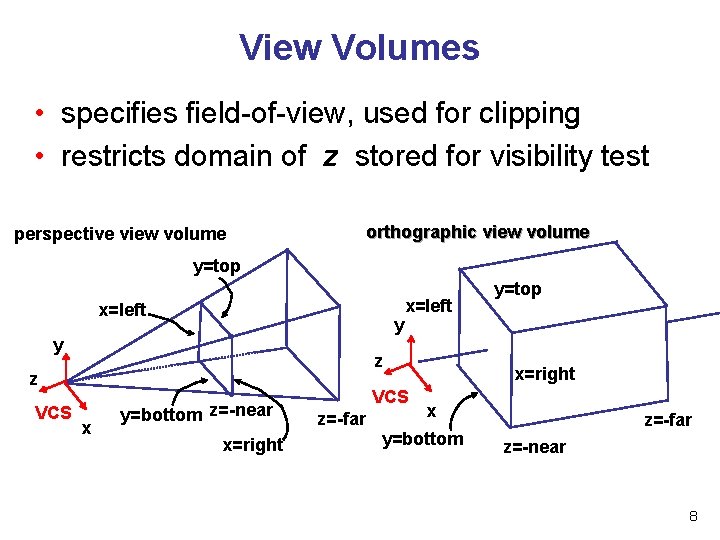
View Volumes • specifies field-of-view, used for clipping • restricts domain of z stored for visibility test orthographic view volume perspective view volume y=top x=left y y z z VCS x=left x y=bottom z=-near x=right VCS z=-far y=top x=right x y=bottom z=-far z=-near 8
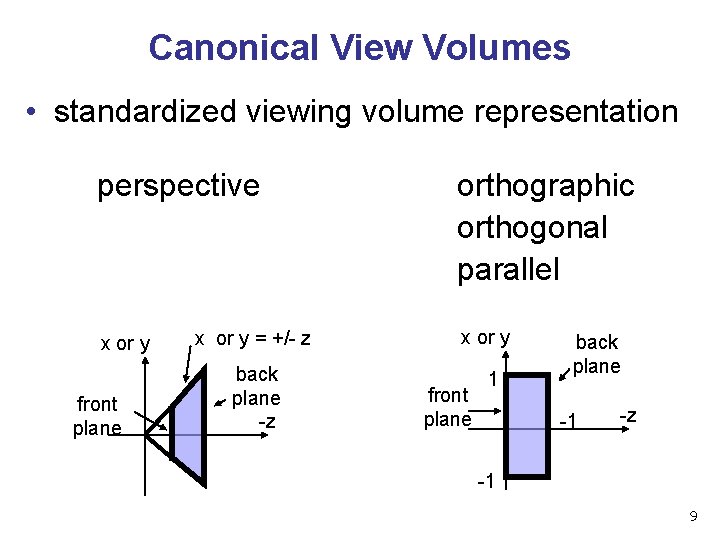
Canonical View Volumes • standardized viewing volume representation perspective x or y front plane x or y = +/- z back plane -z orthographic orthogonal parallel x or y front plane 1 back plane -1 -z -1 9

Why Canonical View Volumes? • permits standardization • clipping • easier to determine if an arbitrary point is enclosed in volume with canonical view volume vs. clipping to six arbitrary planes • rendering • projection and rasterization algorithms can be reused 10

Normalized Device Coordinates • convention • viewing frustum mapped to specific parallelepiped • Normalized Device Coordinates (NDC) • same as clipping coords • only objects inside the parallelepiped get rendered • which parallelepiped? • depends on rendering system 11
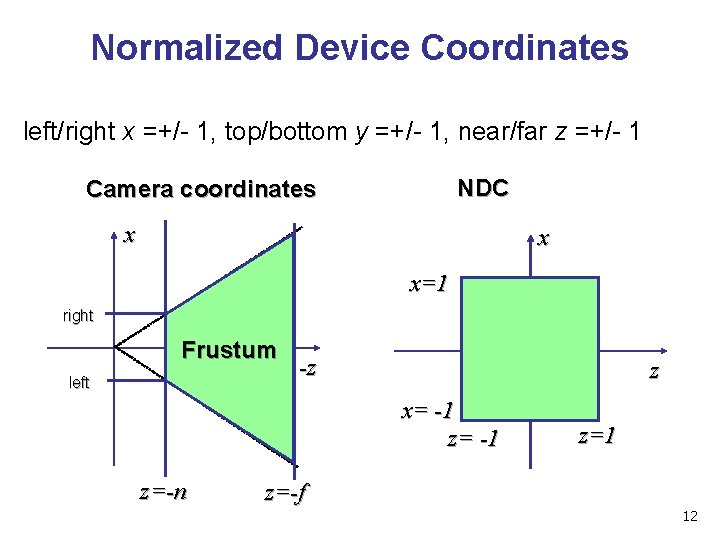
Normalized Device Coordinates left/right x =+/- 1, top/bottom y =+/- 1, near/far z =+/- 1 NDC Camera coordinates x x x=1 right Frustum left -z z x= -1 z=-n z=1 z=-f 12
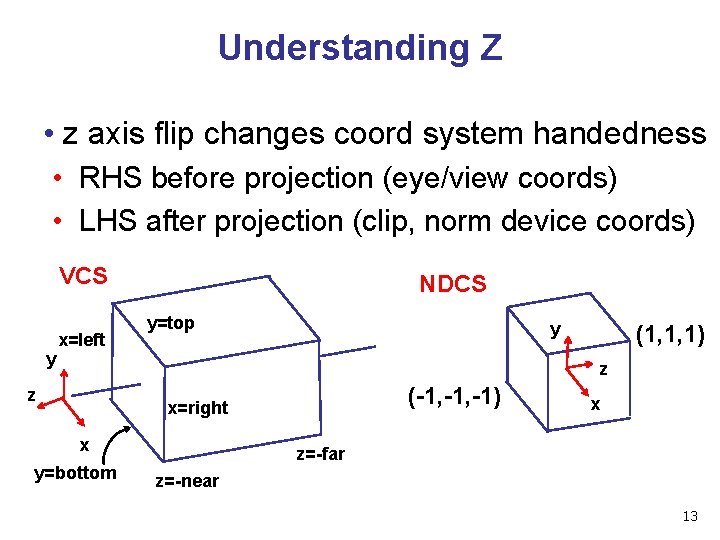
Understanding Z • z axis flip changes coord system handedness • RHS before projection (eye/view coords) • LHS after projection (clip, norm device coords) VCS y x=left NDCS y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 13
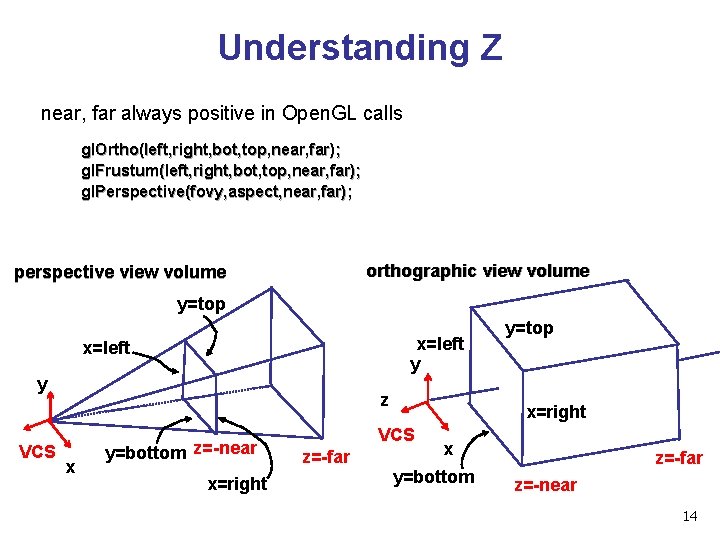
Understanding Z near, far always positive in Open. GL calls gl. Ortho(left, right, bot, top, near, far); gl. Frustum(left, right, bot, top, near, far); gl. Perspective(fovy, aspect, near, far); orthographic view volume perspective view volume y=top x=left y VCS z x y=bottom z=-near x=right VCS z=-far y=top x y=bottom z=-far z=-near 14

Understanding Z • why near and far plane? • near plane: • avoid singularity (division by zero, or very small numbers) • far plane: • store depth in fixed-point representation (integer), thus have to have fixed range of values (0… 1) • avoid/reduce numerical precision artifacts for distant objects 15
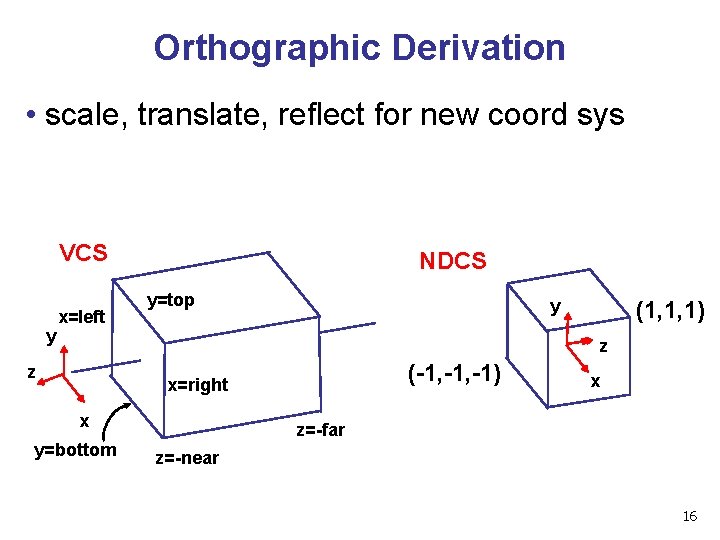
Orthographic Derivation • scale, translate, reflect for new coord sys VCS y x=left NDCS y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 16
Orthographic Derivation • scale, translate, reflect for new coord sys VCS y x=left NDCS y=top y (1, 1, 1) z z (-1, -1) x=right x y=bottom x z=-far z=-near 17

Orthographic Derivation • scale, translate, reflect for new coord sys 18
Orthographic Derivation • scale, translate, reflect for new coord sys VCS y x=left z y=top x=right x y=bottom z=-far z=-near same idea for right/left, far/near 19

Orthographic Derivation • scale, translate, reflect for new coord sys 20

Orthographic Derivation • scale, translate, reflect for new coord sys 21

Orthographic Derivation • scale, translate, reflect for new coord sys 22

Orthographic Derivation • scale, translate, reflect for new coord sys 23

Orthographic Open. GL gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); gl. Ortho(left, right, bot, top, near, far); 24

Demo • Brown applets: viewing techniques • parallel/orthographic cameras • projection cameras • http: //www. cs. brown. edu/exploratories/free. Software/catalogs /viewing_techniques. html 25

Projections II 26
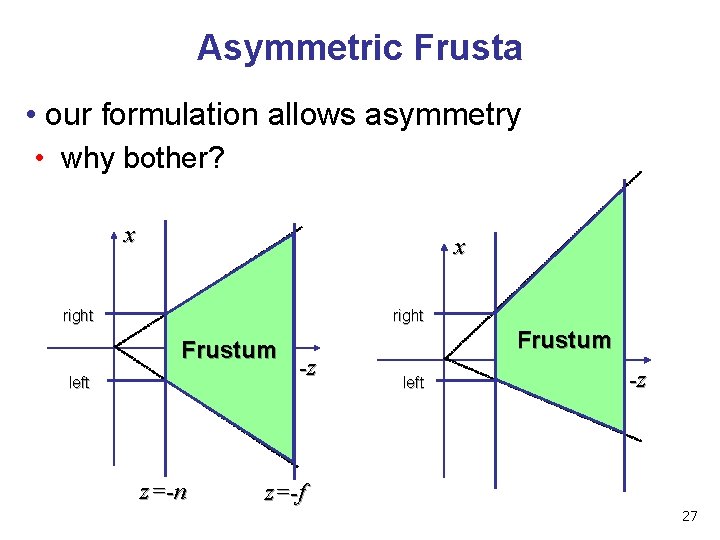
Asymmetric Frusta • our formulation allows asymmetry • why bother? x x right Frustum left z=-n -z Frustum left -z z=-f 27
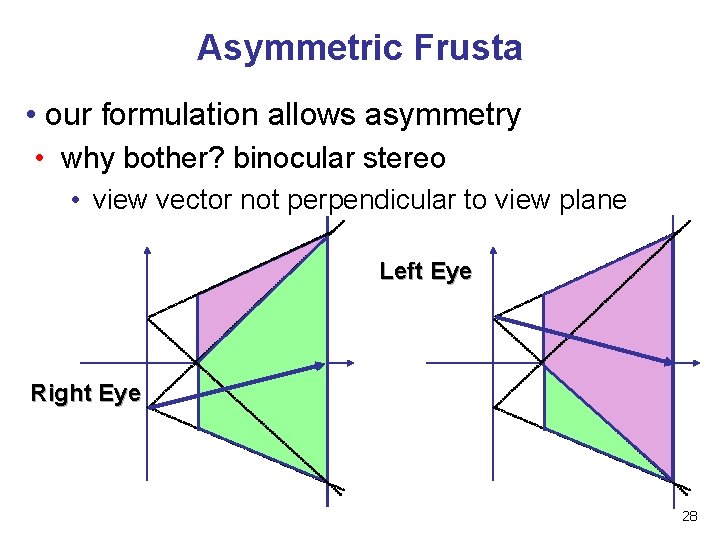
Asymmetric Frusta • our formulation allows asymmetry • why bother? binocular stereo • view vector not perpendicular to view plane Left Eye Right Eye 28

Simpler Formulation • left, right, bottom, top, near, far • nonintuitive • often overkill • look through window center • symmetric frustum • constraints • left = -right, bottom = -top 29
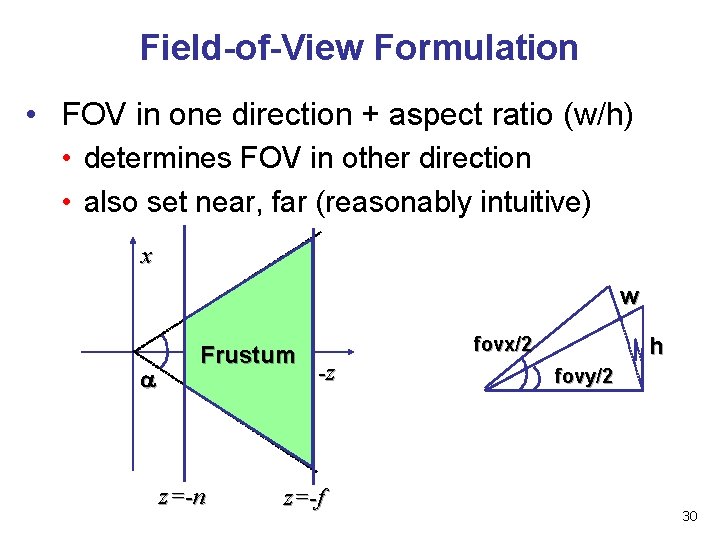
Field-of-View Formulation • FOV in one direction + aspect ratio (w/h) • determines FOV in other direction • also set near, far (reasonably intuitive) x w Frustum z=-n h fovx/2 -z z=-f fovy/2 30

Perspective Open. GL gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); gl. Frustum(left, right, bot, top, near, far); or gl. Perspective(fovy, aspect, near, far); 31

Demo: Frustum vs. FOV • Nate Robins tutorial (take 2): • http: //www. xmission. com/~nate/tutors. html 32
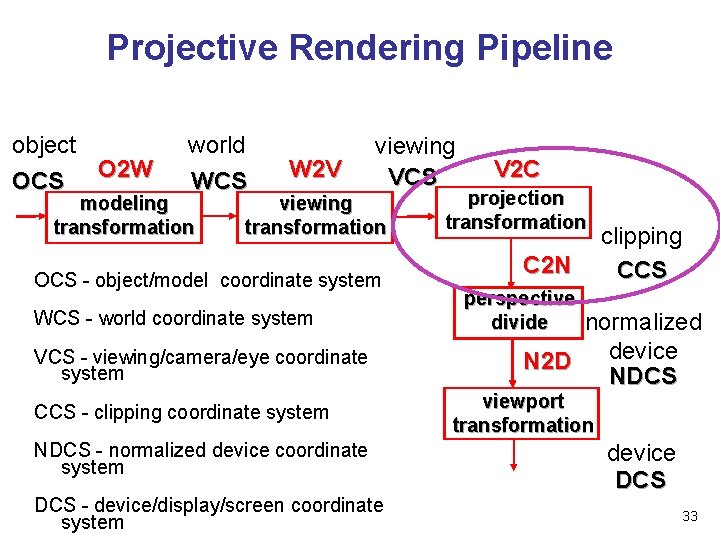
Projective Rendering Pipeline object OCS O 2 W world WCS modeling transformation W 2 V viewing VCS viewing transformation OCS - object/model coordinate system WCS - world coordinate system VCS - viewing/camera/eye coordinate system CCS - clipping coordinate system NDCS - normalized device coordinate system DCS - device/display/screen coordinate system V 2 C projection transformation C 2 N clipping CCS perspective divide normalized device N 2 D NDCS viewport transformation device DCS 33
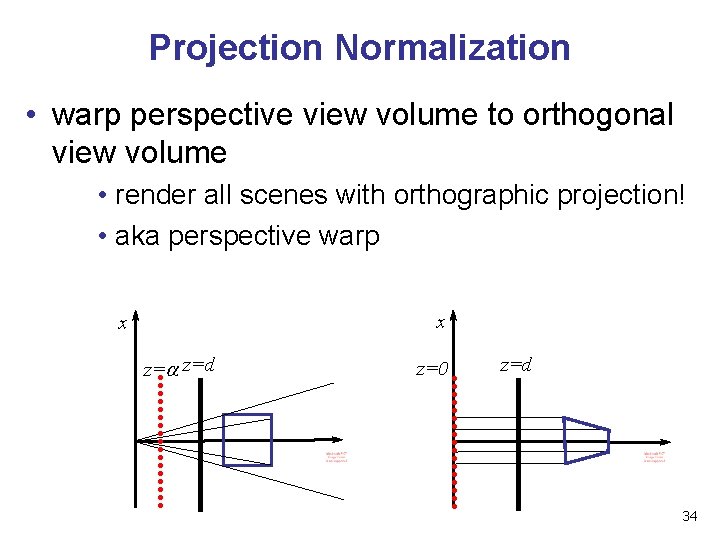
Projection Normalization • warp perspective view volume to orthogonal view volume • render all scenes with orthographic projection! • aka perspective warp x x z= z=d z=0 z=d 34
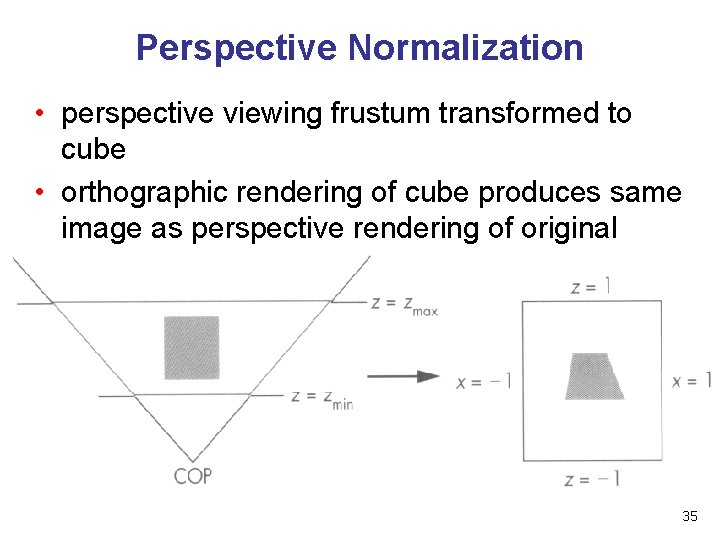
Perspective Normalization • perspective viewing frustum transformed to cube • orthographic rendering of cube produces same image as perspective rendering of original frustum 35
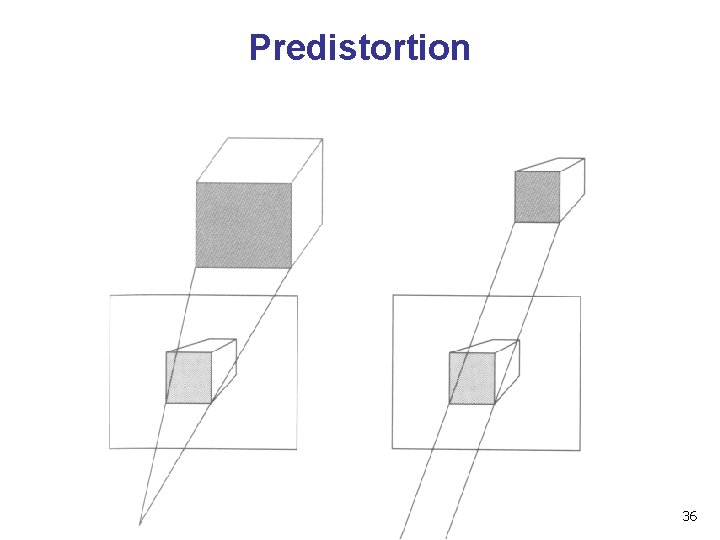
Predistortion 36

Demos • Tuebingen applets from Frank Hanisch • http: //www. gris. uni-tuebingen. de/projects/grdev/doc/html/etc/ Applet. Index. html#Transformationen 37
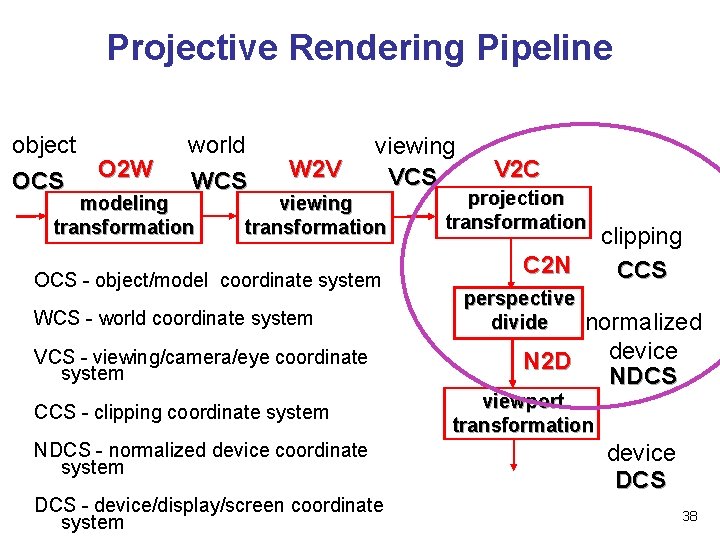
Projective Rendering Pipeline object OCS O 2 W world WCS modeling transformation W 2 V viewing VCS viewing transformation OCS - object/model coordinate system WCS - world coordinate system VCS - viewing/camera/eye coordinate system CCS - clipping coordinate system NDCS - normalized device coordinate system DCS - device/display/screen coordinate system V 2 C projection transformation C 2 N clipping CCS perspective divide normalized device N 2 D NDCS viewport transformation device DCS 38

Separate Warp From Homogenization viewing VCS V 2 C normalized device C 2 N NDCS perspective clipping CCS projection transformation alter w perspective division /w • warp requires only standard matrix multiply • distort such that orthographic projection of distorted objects is desired persp projection • w is changed • clip after warp, before divide • division by w: homogenization 39

Perspective Divide Example • specific example • assume image plane at z = -1 • a point [x, y, z, 1]T projects to [-x/z, -y/z, -z/z, 1]T [x, y, z, -z]T -z 40

Perspective Divide Example • after homogenizing, once again w=1 projection transformation alter w perspective division /w 41

Perspective Normalization • matrix formulation • warp and homogenization both preserve relative depth (z coordinate)

Demo • Brown applets: viewing techniques • parallel/orthographic cameras • projection cameras • http: //www. cs. brown. edu/exploratories/free. Software/catalogs /viewing_techniques. html 43
- Slides: 43