University of British Columbia An Introduction to Computer

University of British Columbia An Introduction to Computer Animation Michiel van de Panne © MIchiel van de Panne

Overview University of British Columbia (1) Creating Animations (2) Representing Rotations © Michiel van de Panne

(1) Creating Animations University of British Columbia algorithm (parameterized models, physics, optimization) user (keyframes) data (motion capture) © Michiel van de Panne

Representing motion University of British Columbia • DOF vs time • cubic polynomial curves x smooth fast in-out t linear • alternative for motion through space: y + v apply arc-length x reparameterization t © Michiel van de Panne

(2) Representing Rotations University of British Columbia world torso LUleg RUleg LUarm RUarm LLleg RLleg LLarm RLarm Lfoot Rfoot Lhand Rhand head trans(0. 30, 0, 0) rot(z, ) © Michiel van de Panne

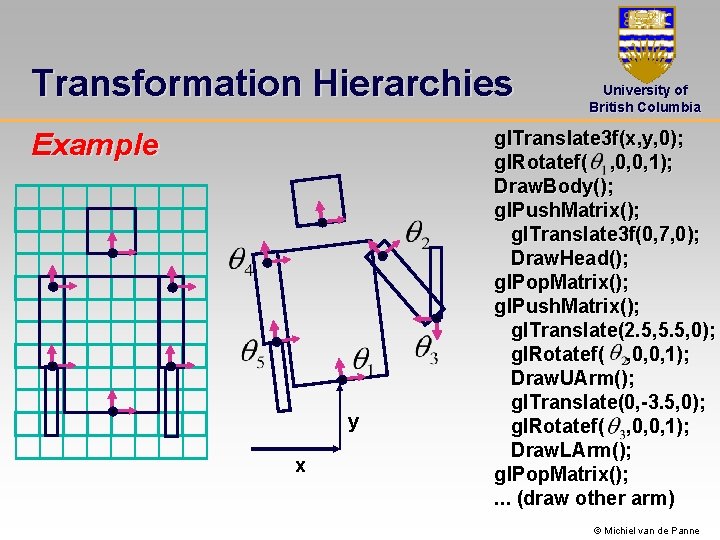
Transformation Hierarchies Example y x University of British Columbia gl. Translate 3 f(x, y, 0); gl. Rotatef( , 0, 0, 1); Draw. Body(); gl. Push. Matrix(); gl. Translate 3 f(0, 7, 0); Draw. Head(); gl. Pop. Matrix(); gl. Push. Matrix(); gl. Translate(2. 5, 5. 5, 0); gl. Rotatef( , 0, 0, 1); Draw. UArm(); gl. Translate(0, -3. 5, 0); gl. Rotatef( , 0, 0, 1); Draw. LArm(); gl. Pop. Matrix(); . . . (draw other arm) © Michiel van de Panne

Rotation DOFs • • • 2 D: 3 D: 4 D: University of British Columbia 1 DOF 3 DOF 6 DOF © Michiel van de Panne

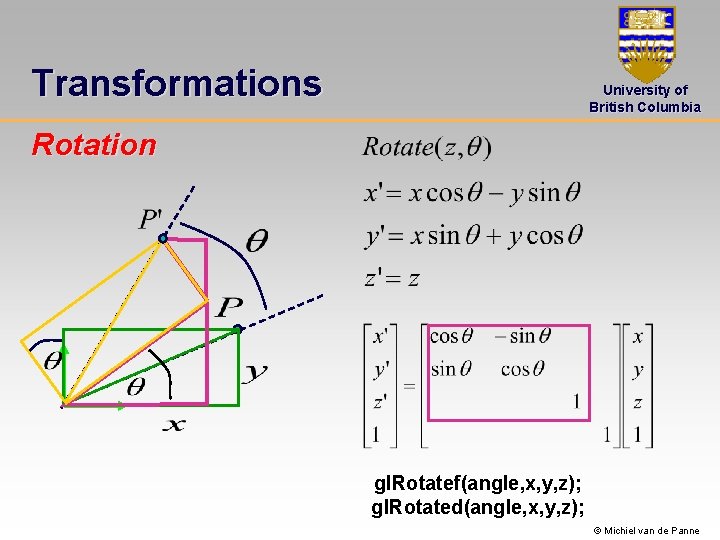
Transformations University of British Columbia Rotation gl. Rotatef(angle, x, y, z); gl. Rotated(angle, x, y, z); © Michiel van de Panne

3 x 3 Rotation Matrix University of British Columbia © Michiel van de Panne

3 x 3 Rotation Matrix • • University of British Columbia 9 elements 6 constraints renormalization algorithms extracting pure rotational component (polar decomp) . . . and determinant = 1 © Michiel van de Panne

Rotations University of British Columbia SO(3) • rotations do not commute • require at least 4 parameters for a smooth parameterization – analogy: surface of the earth 82 D surface, 3 params • combing the hairy ball – camera orientation: view object from any dir © Michiel van de Panne

Rotations • • University of British Columbia orientation vs rotation? how to specify? how to interpolate? 2 D vs 3 D © Michiel van de Panne

Fixed Angle Representations University of British Columbia • fixed sequence of 3 rotations – RPY orientation: roll pitch yaw • can use many ordering of axes • Euler angles: © Michiel van de Panne

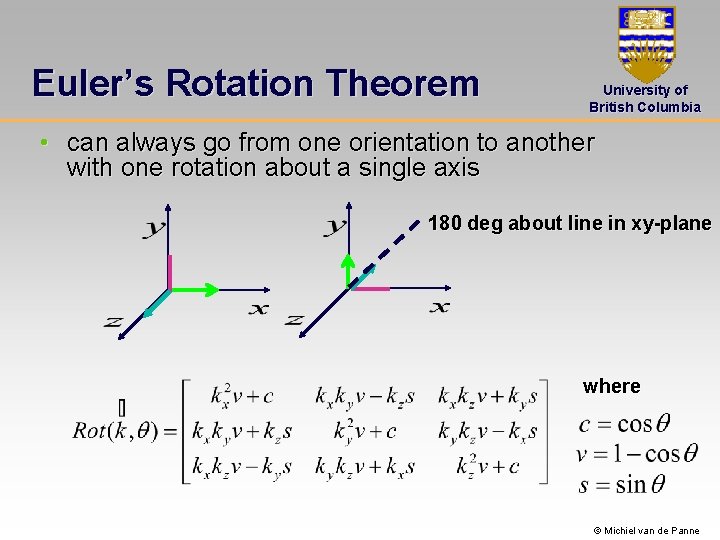
Euler’s Rotation Theorem University of British Columbia • can always go from one orientation to another with one rotation about a single axis 180 deg about line in xy-plane where © Michiel van de Panne

Quaternions University of British Columbia • review of complex numbers • quaternions © Michiel van de Panne

Quaternions University of British Columbia • rotation of a vector • two successive rotations © Michiel van de Panne

Quaternions University of British Columbia RH rule • unit quaternions • addition • multiplication © Michiel van de Panne