Universiteti i Prishtins Fakulteti Ekonomik Studimet pasdiplomike Master

Universiteti i Prishtinës Fakulteti Ekonomik Studimet pasdiplomike / Master Lënda: Mikroekonomi e avancuar 4. Inputet dhe funksioni prodhimit

1. Funksioni prodhimit • Produkti mesatar dhe marxhinal · Izokuantat · Norma marxhinale e zëvendësimit teknik · Elasticiteti I zëvendësimit 2. Disa forma të veçanta të funksionit të prodhimit 3. Të ardhurat e shkallës 4. Progresi teknologjik

Funksioni i prodhimit tregon se cila është sasia maksimale e produktit që mund të realizohet me një sasi të dhënë të inputeve apo cila është sasia minimale e inputeve që duhet të përdorë firma për të prodhuar një sasi të dhënë produkti. Funksioni i prodhimit shpreh lidhjen mes inputeve të përdorura dhe produktit të prodhuar. Kjo lidhje shprehet me ekuacionin: Q=f (L, K)

Ashtu sikurse funksioni i dobisë në teorinë konsumatore që varet nga faktorët ekzogjen (si shija konsumatore) edhe funksioni i prodhimit varet nga kushtet e jashtme teknologjike (progresi teknologjik). • Funksioni i prodhimit në periudhë afatshkurtër • Funksioni i prodhimit në periudhë afatgjatë

Sasia e autputit (njësi për vit) Në periudhë afatshkurtër teknologjia do të merret e pandryshuar që do të thotë Q=f(L). Teknikisht efiçiente (A, B) Q=f(L) B A Sasia maksimale e mundshme e autputit nga niveli dhënë i inputeve D C Teknikisht joefiçiente (C, D) L (njësitë e punës për vit) Fig. 1. Efiçenca dhe joefiçenca teknike

ðFigura na tregon funksionin e prodhimit për një input Q=f(L) ðNë të kundërtën L=g(Q) ðNëse Q=√L atëherë L=Q² ðNëse Q=7, atëherë L=7²=49, që do të thotë se për të prodhuar autputin prej 7 njësi do të nevojiten 49 njësi punë. ðMeqenëse firma mund të prodhoj më pak se sa niveli I mundshëm i autputit, ekuacioni mund të shkruhet edhe në këtë mënyrë: Q ≤ f(L, K)

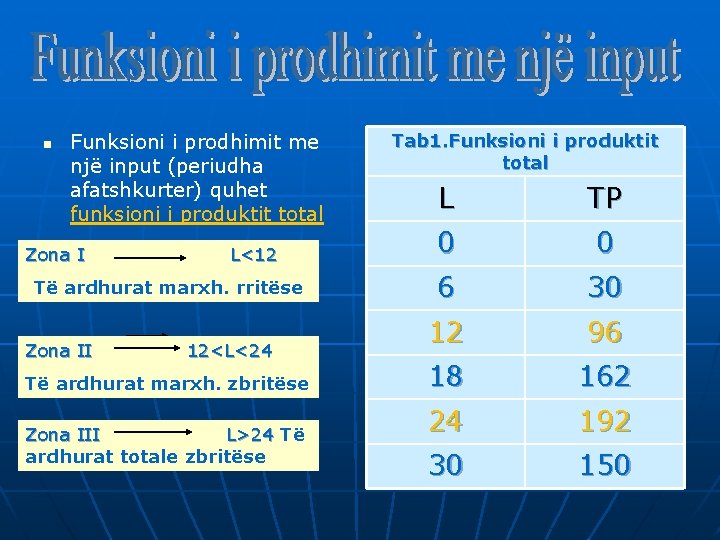
n Funksioni i prodhimit me një input (periudha afatshkurter) quhet funksioni i produktit total Zona I L<12 Të ardhurat marxh. rritëse Zona II 12<L<24 Të ardhurat marxh. zbritëse Zona III L>24 Të ardhurat totale zbritëse Tab 1. Funksioni i produktit total L TP 0 0 6 30 12 96 18 162 24 192 30 150

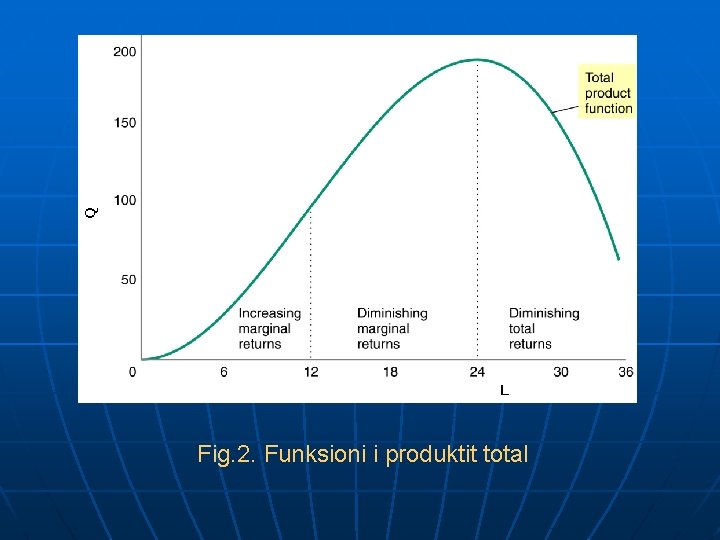
Q L Fig. 2. Funksioni i produktit total

Produkti mesatar: AP = TP/L (produkti total / sasia e punës) Tab. 1. Funksioni i produktit total L TP AP 6 30 5 12 96 8 18 162 9 24 192 8 30 150 5 max.

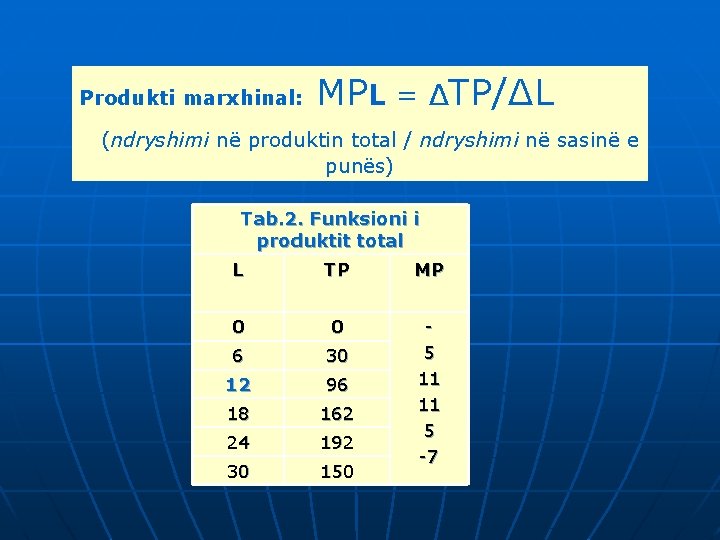
Produkti marxhinal: MPL = ΔTP/ΔL (ndryshimi në produktin total / ndryshimi në sasinë e punës) Tab. 2. Funksioni i produktit total L TP MP 0 0 6 30 12 96 18 162 24 192 30 150 5 11 11 5 -7

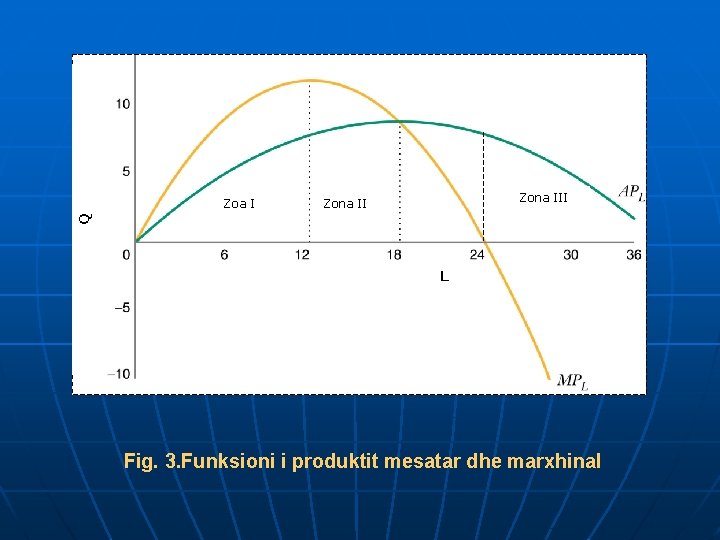
Zona III Zona II Q Zoa I L Fig. 3. Funksioni i produktit mesatar dhe marxhinal

Në zonën e të ardhurave marxhinale rritëse (zona parë), produkti marxhinal i punës do të rritet. Në zonën e të ardhurave marxhinale zbritëse (zona e dytë), produkti marxhinal i punës do të zvogëlohet. Në këtë zonë, produkti marxhinal i punës barazohet me produktin mesatar (derisa produkti mesatar i punës është në maksimum). Në zonën e të ardhurave totale zbritëse (zona e tretë), produkti marxhinal i punës ndërpret boshtin x dhe bëhet negative.

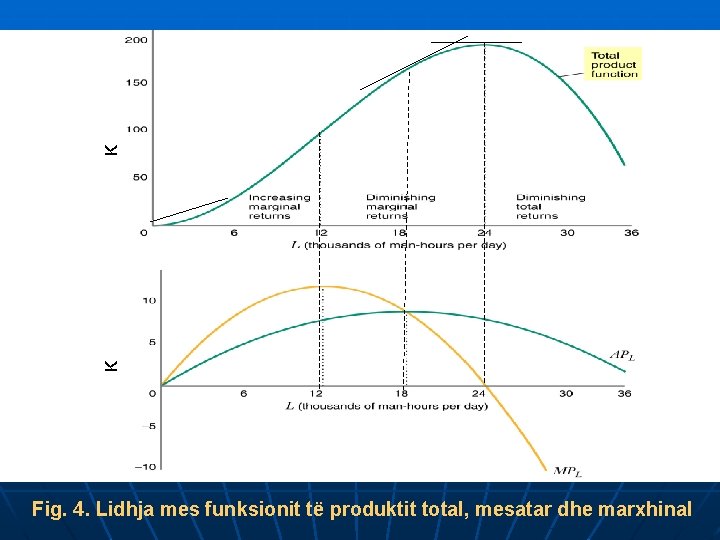
K K K MPL= 0 LL Fig. 4. Lidhja mes funksionit të produktit total, mesatar dhe marxhinal

Produkti marxhinal i punës në çdo pikë është i barabartë me pjerrësinë e produktit total në atë pikë. Produkti mesatar i punës në çdo pikë është i barabartë me pjerrësinë e drejtëzës nga origjina në produktin total në atë pikë. Në zonën e të ardhurave marxhinale rritëse (zona parë), produkti marxhinal i punës do të rritet. Në zonën e të ardhurave marxhinale zbritëse (zona e dytë), produkti marxhinal i punës do të zvogëlohet. Në zonën e të ardhurave totale zbritëse (zona e tretë), produkti marxhinal i punës ndërpret boshtin x dhe bëhet negative.

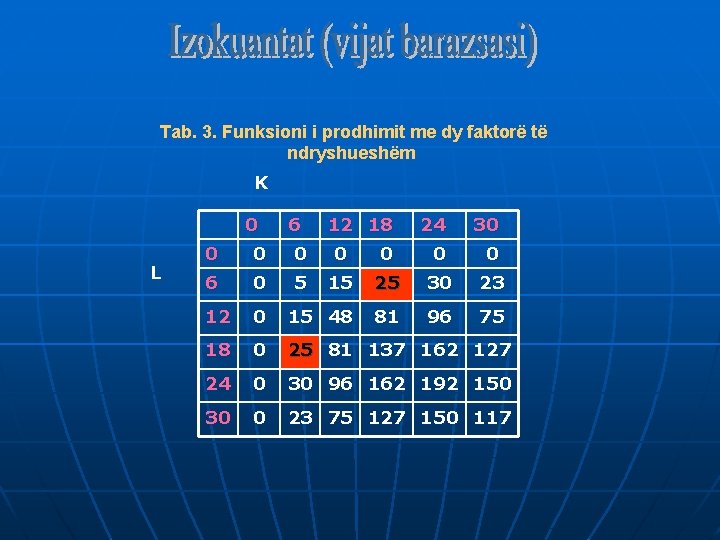
Q=f (L, K) Tab. 3. Funksioni i prodhimit (L, K) K 0 L 6 12 18 24 30 0 0 0 6 0 5 15 25 30 23 12 0 15 48 81 96 75 18 0 25 81 137 162 127 24 0 30 96 162 192 150 30 0 23 75 127 150 117

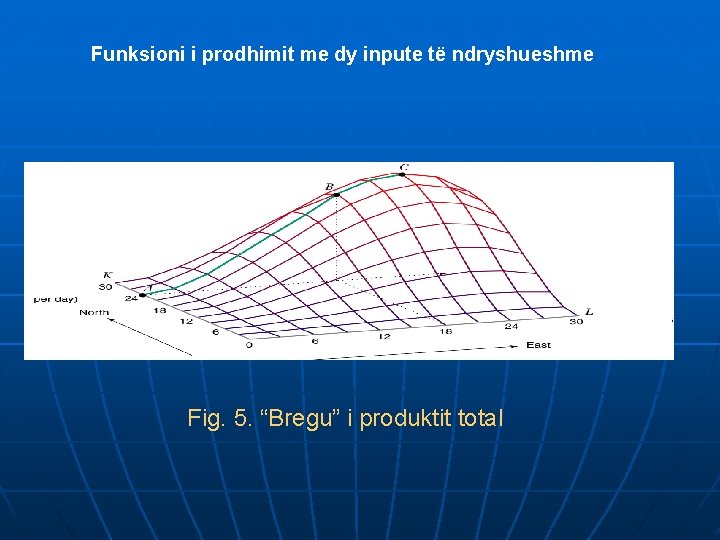
Funksioni i prodhimit me dy inpute të ndryshueshme Fig. 5. “Bregu” i produktit total

Produkti marxhinal MPL = TP/ L (duke mbajtur të gjitha inputet tjera konstant) MPK = TP/ K (duke mbajtur të gjitha inputet tjera konstant)

Tab. 3. Funksioni i prodhimit me dy faktorë të ndryshueshëm K 0 L 6 12 18 24 30 0 0 0 6 0 5 15 25 30 23 12 0 15 48 81 96 75 18 0 25 81 137 162 127 24 0 30 96 162 192 150 30 0 23 75 127 150 117

Të gjitha kombinimet (L, K) japin autputin prej 25 njësi K Më shumë autput L Fig. 7. Izokuantat dhe funksioni i prodhimit

Definimi: Një izokunat (vija barazsasi) paraqet të gjitha kombinimet e inputeve (punës dhe kapitalit) që i mundësojnë firmës të prodhojë nivelin e njejtë të sasisë së autputit. Shembull: Q= K½ L ½ Çfarë është ekuacioni i izokuantës nëse Q=20? 20 = K½ L ½ → 400=KL→K=400/L

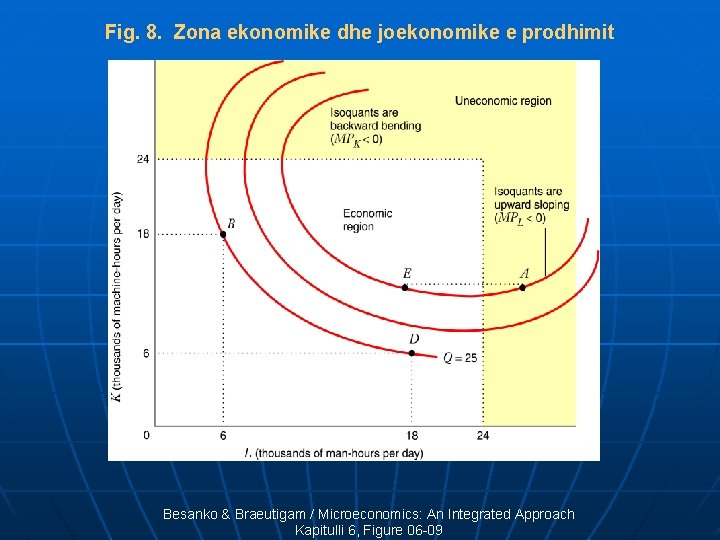
Fig. 8. Zona ekonomike dhe joekonomike e prodhimit Besanko & Braeutigam / Microeconomics: An Integrated Approach Kapitulli 6, Figure 06 -09

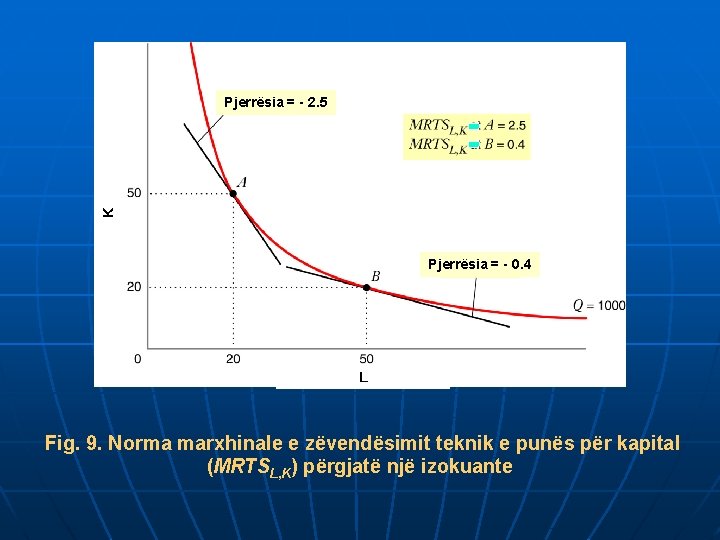
Norma marxhinale e zëvendësimit teknik (MRTSL, K) tregon: • Normën në të cilën sasia e kapitalit duhet zvogëluar për çdo rritje të njësie të punës, duke mbajtur sasinë e autputit konstant. • Normën në të cilën sasia e kapitalit duhet rritur për çdo zvogëlim të njësie të punës, duke mbajtur sasinë e autputit konstant.

K Pjerrësia = - 2. 5 Pjerrësia = - 0. 4 L Fig. 9. Norma marxhinale e zëvendësimit teknik e punës për kapital (MRTSL, K) përgjatë një izokuante

Ndryshimet e K dhe L mbajnë të pandryshuar autputin përgjatë një izokuante ΔQ= ( K X MPK) + ( L X MPL) 0 =( K X MPK) + ( L X MPL) => - K/ L = MPL/MPK = MRTSL, K

Nëse produktet marxhinale janë pozitive, pjerrësia e izokuantës është negative. . . Nëse kemi të ardhura marxhinale zbritëse, gjithashtu kemi MRST zbritëse. Për disa funksione prodhimi, produkti marxhinal mund të bëhet negativ. Kjo është zona joekonomike e hartës së izokuantave.

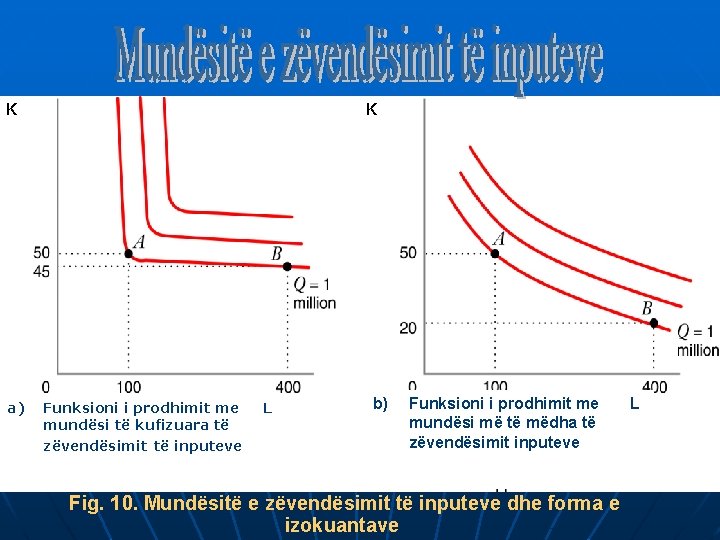
K K a) Funksioni i prodhimit me mundësi të kufizuara të zëvendësimit të inputeve L b) Funksioni i prodhimit me mundësi më të mëdha të zëvendësimit inputeve Fig. 10. Mundësitë e zëvendësimit të inputeve dhe forma e izokuantave L

a)Kur funksioni i prodhimit ofron mundësi të kufizuara të zëvendësimit, MRTS(L, K) ndryshon dukshëm kur lëvizim përgjat izokuantës. Izokuantat kanë afërsisht formën “L” b) Kur funksioni i prodhimit ofron mundësi më të mëdha të zëvendësimit, MRTS(L, K) ndryshon gradualisht kur lëvizim përgjat izokuantës. Izokuantat janë afërsisht linja të drejta.

σ= Përqindja e ndryshimit në normën K/L Përqindja e ndryshimit në MRTS (L, K) σ= % Δ (K/L) % Δ MRTS (L, K)

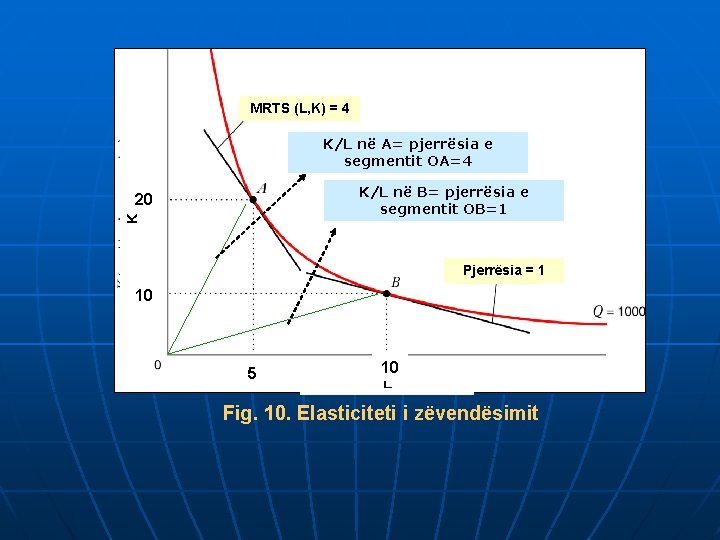
MRTS (L, K) = 4 K/L në A= pjerrësia e segmentit OA=4 K/L në B= pjerrësia e segmentit OB=1 K 20 Pjerrësia = 1 10 5 10 L Fig. 10. Elasticiteti i zëvendësimit

Në pikën A, MRTS=4, kurse në pikën B, MRTS=1 që do të thotë se ΔMRTS=1 -4=-3 % Δ MRTS (L, K)= Δ MRTS (L, K) X 100 = -3 = - 75 4 Δ K/L= 1 -4=-3 % Δ K/L= -3/4 x 100=-75 Përqindja e ndryshimit në normën K/L është (-75), por edhe përqindja e ndryshimit në MRTS (L, K) është (-75), kështu që elasticiteti i zëvendësimit prej pikës A deri në pikën B është σ= 1.

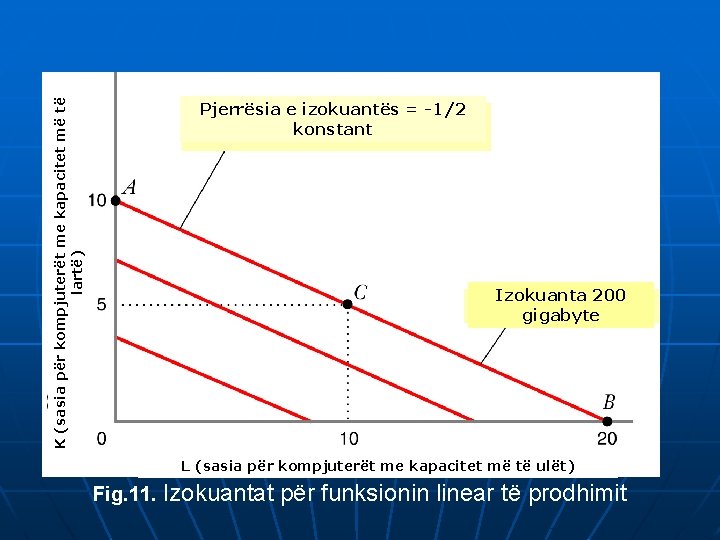
1. Funksioni linear i prodhimit: Q = a. L + b. K · MRTS konstante · Të ardhurat e shkallës konstante · =

K (sasia për kompjuterët me kapacitet më të lartë) Pjerrësia e izokuantës = -1/2 konstant Izokuanta 200 gigabyte L (sasia për kompjuterët me kapacitet më të ulët) Fig. 11. Izokuantat për funksionin linear të prodhimit

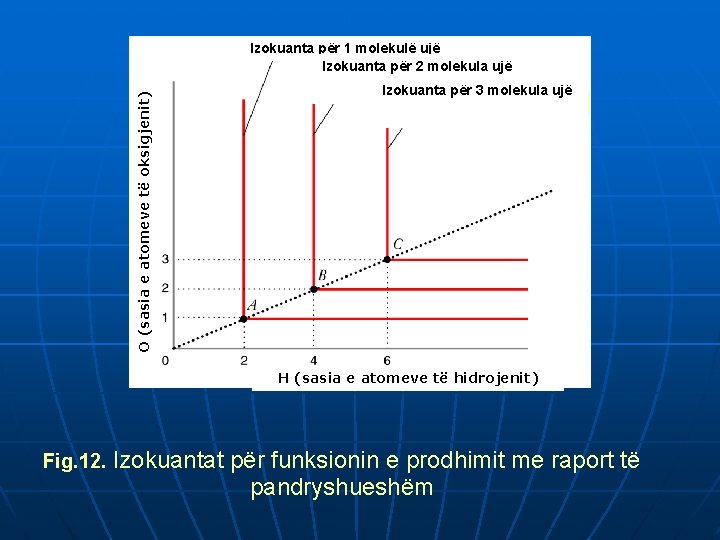
2. Funksioni pandryshuar Leontief): i prodhimit me raport të (Funksioni i prodhimit • Q=min (a. L, b. K) • Izokuantat e formës “L” • MRTS ndryshon (∞ deri 0) • σ =0

O (sasia e atomeve të oksigjenit) Izokuanta për 1 molekulë ujë Izokuanta për 2 molekula ujë Izokuanta për 3 molekula ujë H (sasia e atomeve të hidrojenit) Fig. 12. Izokuantat për funksionin e prodhimit me raport të pandryshueshëm

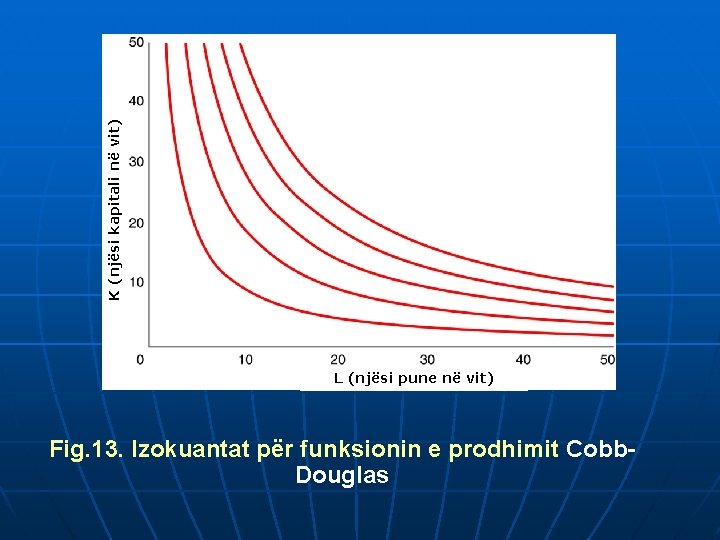
3. Funksioni i prodhimit Cobb-Douglas Q = a L K ð Për dallim nga funksioni I prodhimit linear, norma me të cilën L zëvendësohet me K nuk është konstante ð Për dallim nga funksioni I prodhimit me raporte të pandryshueshme, norma me të cilën L zëvendësohet me K është e ndryshueshme. ð MRTS ndryshon prej 0 në ∞, në fakt saktësisht është 1. ð Izokuanta janë kurba jolineare me pjerrësi zbritëse. ð =1

K (njësi kapitali në vit) L (njësi pune në vit) Fig. 13. Izokuantat për funksionin e prodhimit Cobb. Douglas

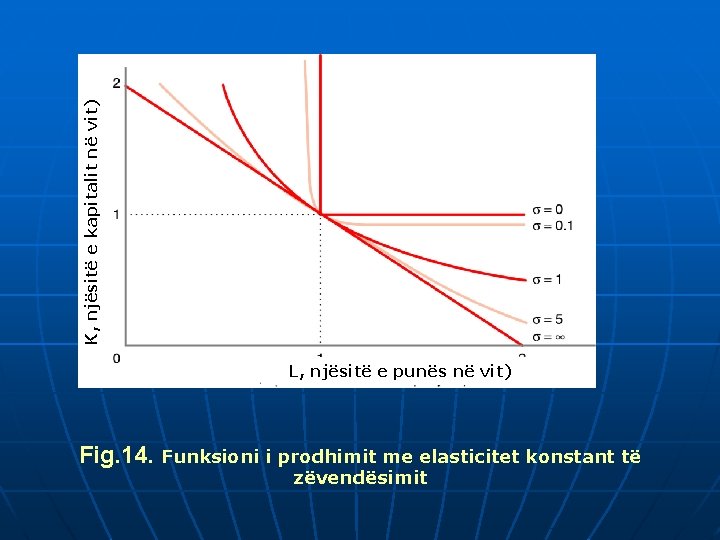
3. Funksioni i prodhimit me elasticitet konstant të zëvedësimit Q = [a. L +b. K ]1/ , ku = ( -1)/ Funksioni I prodhimit Leontief (bashkëplotësuesit e plotë): = 0. Funksioni I prodhimit Cobb-Douglas: = 1 Funksioni I prodhimit linear (zëvendësuesit e plotë): = , Funksioni I prodhimit me elasticitet konstant të zëvendësimit: mes 0 dhe

K, njësitë e kapitalit në vit) L, njësitë e punës në vit) Fig. 14. Funksioni i prodhimit me elasticitet konstant të zëvendësimit

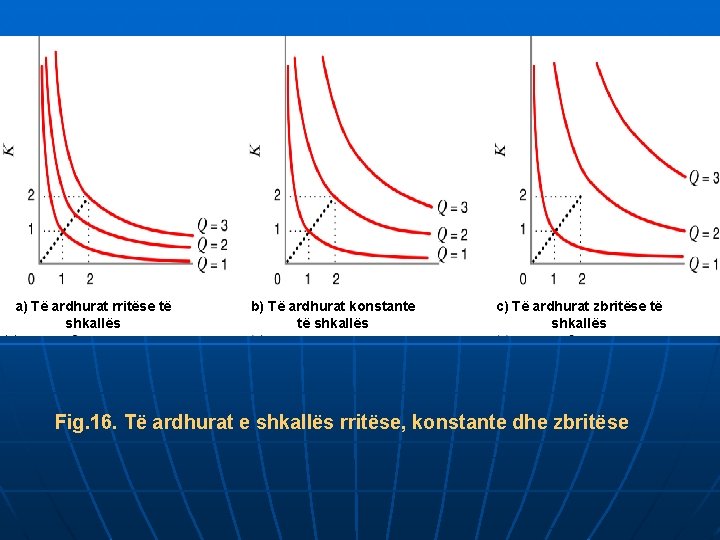
Të diskutohet lidhur me të ardhurat e shkallës (rritëse, konstante, zbritëse)

a) Të ardhurat rritëse të shkallës b) Të ardhurat konstante të shkallës c) Të ardhurat zbritëse të shkallës Fig. 16. Të ardhurat e shkallës rritëse, konstante dhe zbritëse

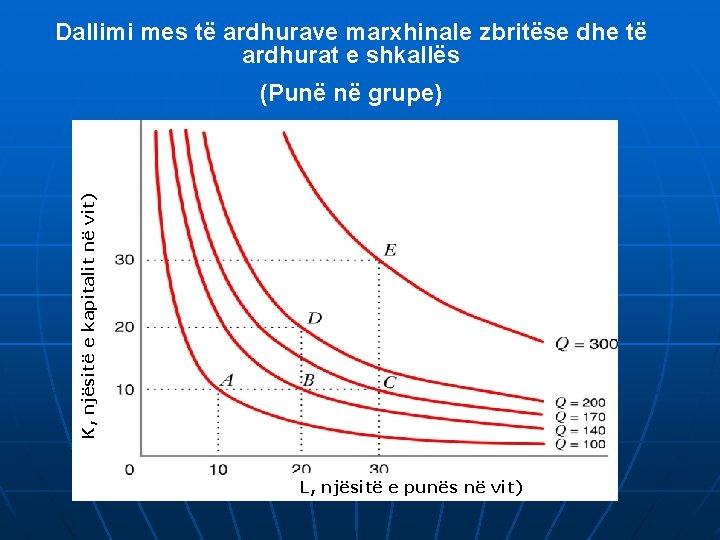
Dallimi mes të ardhurave marxhinale zbritëse dhe të ardhurat e shkallës K, njësitë e kapitalit në vit) (Punë në grupe) L, njësitë e punës në vit)

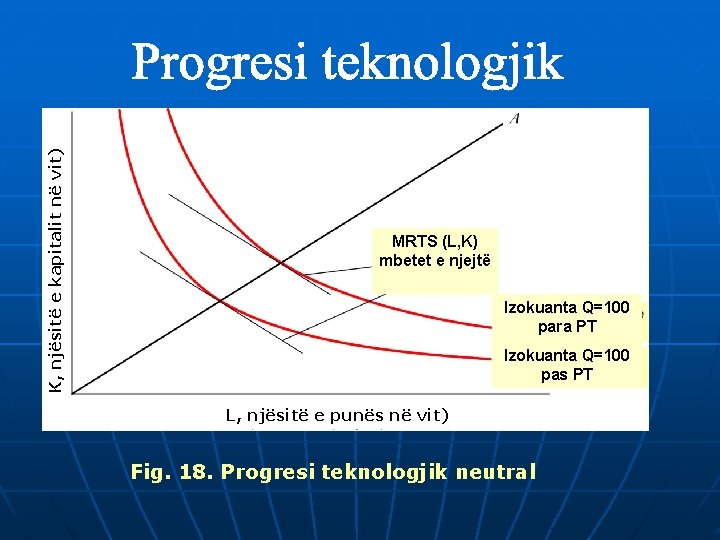
K, njësitë e kapitalit në vit) MRTS (L, K) mbetet e njejtë Izokuanta Q=100 para PT Izokuanta Q=100 pas PT L, njësitë e punës në vit) Fig. 18. Progresi teknologjik neutral

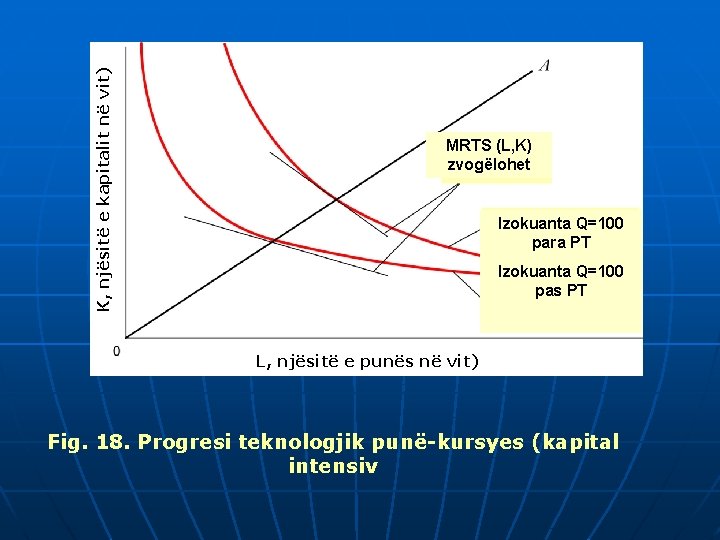
K, njësitë e kapitalit në vit) MRTS (L, K) zvogëlohet Izokuanta Q=100 para PT Izokuanta Q=100 pas PT L, njësitë e punës në vit) Fig. 18. Progresi teknologjik punë-kursyes (kapital intensiv

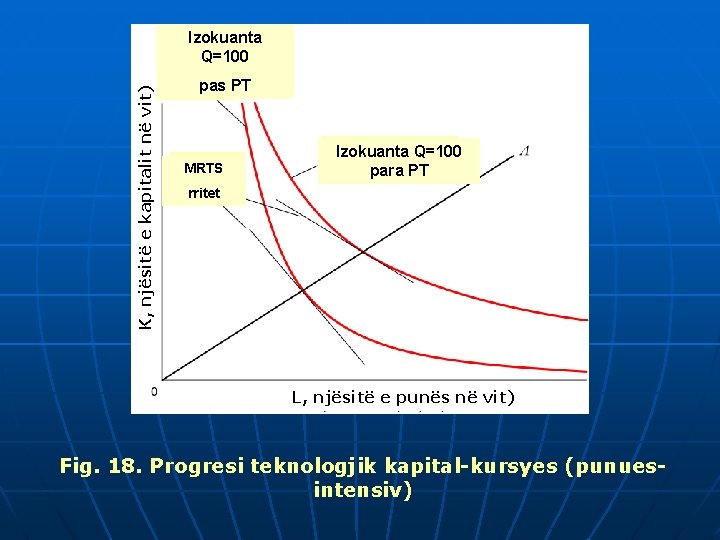
K, njësitë e kapitalit në vit) Izokuanta Q=100 pas PT MRTS Izokuanta Q=100 para PT rritet L, njësitë e punës në vit) Fig. 18. Progresi teknologjik kapital-kursyes (punuesintensiv)

n Çështjet e trajtuara gjenden në kreun 6 të librit: “Microeconomics: An Integrated Approach” nga autorët: David A. Besanko dhe Ronald R. Braeutigam, fq. 217 - 294